يتم إعطاء العديد من الأسماء للقوى، مثل قوة الدفع، والسحب، والشد، والوزن. تقليديًا، تم تجميع القوى في عدة فئات وأُعطيت أسماء تتعلق بمصدرها، وكيفية انتقالها، أو آثارها. تمت مناقشة العديد من هذه الفئات في هذا القسم، جنبًا إلى جنب مع بعض التطبيقات المثيرة للاهتمام. مزيد من الأمثلة على القوى تمت مناقشتها لاحقًا في هذا الكتاب.
القوى الشائعة
أهداف التعلم:
بنهاية هذا القسم، ستكون قادرًا على:
- تحديد القوى الطبيعية وقوى التوتر
- التمييز بين القوى الحقيقية والقوى الخيالية
- تطبيق قوانين نيوتن للحركة لحل المسائل التي تنطوي على قوى متنوعة
المحتويات
تصنيف القوى: القوى الطبيعية والتوتر وأمثلة أخرى للقوى
سيكون تصنيف القوى مفيدًا كمرجع لأننا نحل العديد من المسائل التي تتضمن القوة والحركة. تشمل هذه القوى القوة الطبيعية والتوتر والاحتكاك وقوة الزنبرك.
1. القوى الطبيعية
الوزن (يسمى أيضًا قوة الجاذبية) هو قوة شائعة تعمل في جميع الأوقات ويجب مواجهتها لمنع الجسم من السقوط. يجب أن تتحمل وزن جسم ثقيل عن طريق دفعه لأعلى عندما تمسكه ثابتًا، كما هو موضح في الشكل 5.21 (أ). ولكن كيف يمكن للأشياء الجامدة مثل الطاولة أن تدعم وزن الكتلة الموضوعة عليها، كما هو موضح في الشكل 5.21 (ب)؟ عندما يتم وضع كيس طعام الكلاب على الطاولة، تتدلى الطاولة قليلاً تحت الحِمل. سيكون هذا ملحوظًا إذا تم وضع الحمولة على منضدة بطاقات، ولكن حتى طاولة البلوط القوية تنحني عند الضغط عليها بقوة. ما لم ينحني الجسم خارج حدوده، فإنه سيبذل قوة استعادة تشبه إلى حد كبير الزنبرك المنحني (أو الترامبولين أو لوح الغوص). كلما زاد الانحناء، زادت قوة الاستعادة. وهكذا، عندما يتم وضع الحمولة على المنضدة، فإن الطاولة تتدلى حتى تصبح قوة الاستعادة كبيرة مثل وزن الحمولة.
عند هذه النقطة، القوة الخارجية الصافية على الحِمل تساوي صفرًا. هذا هو الوضع عندما يكون الحِمل ثابتًا على الطاولة. تتدلى الطاولة بسرعة ويكون الترهل طفيفًا، لذلك لا نلاحظ ذلك. لكنه يشبه ترهل الترامبولين عندما تصعد عليه.
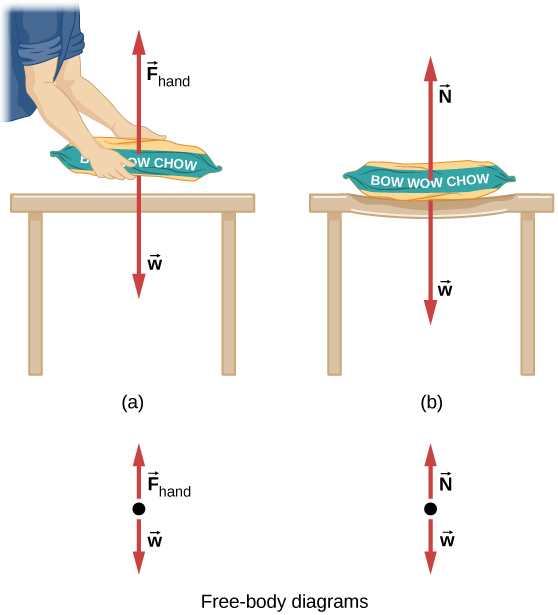
الشكل 5.21 (أ) يجب على الشخص الذي يحمل كيس طعام الكلب أن يمد يده بقوة تصاعدية مساوية في المقدار ومعاكسة في الاتجاه لوزن الطعام بحيث لا يسقط على الأرض. (ب) تتدلى الطاولة عند وضع طعام الكلب عليها، مثل الترامبولين القاسي. تنمو قوى الاستعادة المرنة في الطاولة عندما تتدلى حتى توفر قوة N⃗ مساوية في المقدار ومعاكسة في الاتجاه لوزن الطعام.
معادلة حساب القوة
يجب أن نستنتج أن كل ما يدعم الحِمل، سواء كان متحركًا أم لا، يجب أن يوفر قوة تصاعدية تساوي وزن الحِمل، كما افترضنا في بعض الأمثلة السابقة. إذا كانت القوة الداعمة لوزن جسم، أو حِمل، متعامدة مع سطح التلامس بين الحمل ودعمه، تُعرَّف هذه القوة على أنها قوة عادية، وهنا يُعطى لها الرمز N⃗. (هذه ليست وحدة نيوتن للقوة ، أو N) وكلمة عادي Normal تعني عمودي على سطح. هذا يعني أنه يمكن التعبير عن القوة الطبيعية التي يتعرض لها جسم يستقر على سطح أفقي في شكل متجه على النحو التالي:
N⃗ = −mg⃗.
(5.11)
في الشكل العددي، تصبح هذه المعادلة:
N = − mg
(5.12)
يمكن أن تكون القوة العادية Normal Force أقل من وزن الجسم إذا كان الجسم في منحدر.
مثال 5.12: حساب الوزن عند المنحدر
نفرض أن لدينا المتزلجة على المنحدر في الشكل 5.22. كتلتها بما في ذلك المعدات 60.0 كجم. (أ) ما هو تسارعها إذا كان الاحتكاك ضئيلاً؟ (ب) ما هو تسارعها إذا كان الاحتكاك = 45.0 نويتن N؟
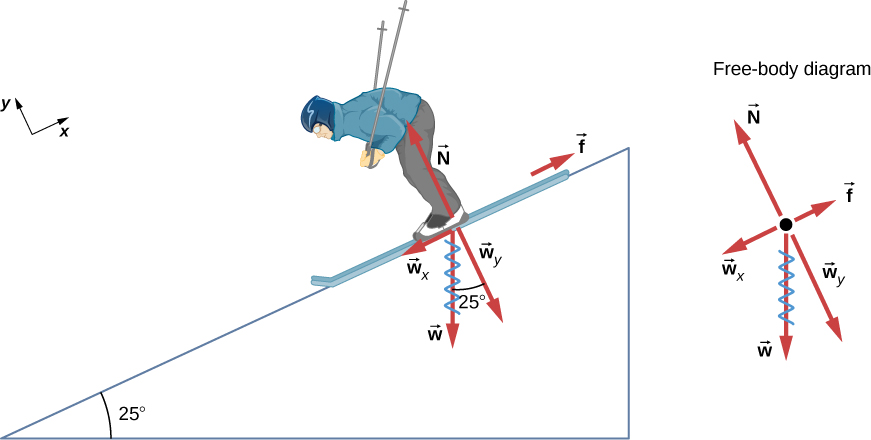
الشكل 5.22: يوضح شخصًا يتزلج على منحدر يميل بزاوية 25 درجة على المحور الأفقي. القوة f لأعلى وموازية لميل المنحدر، والقوة N لأعلى وعمودية على المنحدر. القوة w مباشرة لأسفل. مكونه wx لأسفل وموازي لميل لمنحدر، ومكونه wy لأسفل وعمودي على المنحدر. تظهر كل هذه القوى أيضًا في مخطط الجسم الحر. مع اعتبار المحور X موازيًا للمنحدر.
في الشكل 5.22: نظرًا لأن التسارع موازي لميل المنحدر ويعمل باتجاه أسفل المنحدر، فمن الأنسب عرض كل القوى على نظام إحداثيات حيث يكون أحد المحورين موازٍ لميل المنحدر والآخر متعامد عليه (المحاور موضحة على يسار المتزلج). N⃗ عمودي على الميل و f⃗ موازية للميل، لكن w⃗ لها مكونات على طول كلا المحورين، وهما wy و wx. هنا، يوجد خط متعرج لإظهار أنه قد تم استبداله بهذه المكونات. القوة N⃗ تساوي في المقدار للمكوّن wy، لذا لا يوجد تسارع عمودي على المنحدر. لكن القوة f أقل من المكوّن wx، لذلك يوجد تسارع منحدر لأسفل (على طول المحور الموازي لميل المنحدر).
استراتيجية الحل
هذه مسألة ثنائية الأبعاد، لأن القوى التي تؤثر على المتزلج (نظام الاهتمام) ليست متوازية. النهج الذي استخدمناه في الديناميكا ثنائية الأبعاد يعمل جيدًا هنا أيضًا. اختر نظام إحداثيات مناسبًا واسقط المتجهات على محاوره، مما يخلق مسألتين أحاديتي البعد لحلهما. أكثر أنظمة الإحداثيات ملاءمة للحركة على المنحدر هو النظام الذي يحتوي على إحداثي موازٍ لميل المنحدر وآخر عمودي على المنحدر. (تكون الحركات على طول المحاور المتعامدة بشكل متبادل مستقلة). نستخدم x وy للاتجاهات المتوازية والعمودية، على التوالي.
هذا الاختيار للمحاور يبسط هذا النوع من المسائل، لأنه لا توجد حركة عمودية على المنحدر والتسارع يكون منحدرًا لأسفل. فيما يتعلق بالقوى، يتم رسم الاحتكاك في مواجهة الحركة (الاحتكاك دائمًا يعارض الحركة الأمامية) ويكون دائمًا موازيًا للميل، حيث يتم رسم المكوّن wx للوزن بالتوازي مع ميل المنحدر (يتسبب في حركة المتزلج لأسفل المنحدر)، ويتم رسم المكوّن wy للوزن عموديًا على المنحدر. بعد ذلك، يمكننا النظر في المسائل المنفصلة للقوى الموازية لميل المنحدر والقوى العمودية على المنحدر.
الحل
مقدار مكون الوزن الموازي للمنحدر هو
wx = w sin 25°=m g sin 25°
wx = w sin 25°= m g sin25°,
ومقدار مكون الوزن العمودي على المنحدر هو
wy=w cos 25° = m g cos 25°
wy = w cos 25° = m g cos25°.
أ. عند إهمال الاحتكاك. بما أن العجلة (التسارع) موازي للميل، فلا نحتاج إلا إلى اعتبار القوى الموازية للميل. (القوى المتعامدة مع ميل المنحدر تضاف إلى الصفر، حيث لا يوجد تسارع في هذا الاتجاه). القوى الموازية للميل هي مكون وزن المتزلج الموازي للميل wx والاحتكاك f. باستخدام قانون نيوتن الثاني، مع الرموز المنخفضة للدلالة على الكميات الموازية للمنحدر، يكون لدينا:
a x = Fnet x / m
حيث:
Fne tx = wx = m g sin 25°
وبافتراض عدم وجود احتكاك في هذا الجزء من المسألة. وبالتالي يكون التسارع هو:
a x = Fnet x / m = m g sin 25° / m = g sin 25°
ب. نقوم بتضمين الاحتكاك. لدينا قيمة معطاة للاحتكاك، ونعلم أن اتجاهه موازٍ لميل المنحدر ويعارض الحركة بين الأسطح المتلامسة. إذن القوة الخارجية الصافية هي:
Fne tx = wx – f
بالتعويض بهذه القيمة في قانون نيوتن الثاني، ax = Fnetx / m، يعطينا:
a x = Fnet x / m = ( wx – f ) / m = ( m g sin 25° – f ) / m
نقوم بالتعويض عن القيم المعروفة ونحصل على:
a x = Fnet x / m = ( wx – f ) / m = ( m g sin 25° – f ) / m
ax=(60.0kg)(9.80m/s2)(0.4226)−45.0N60.0kg.ax=(60.0kg)(9.80m/s2)(0.4226)−45.0N60.0kg.
التسارع (a) = 3.39 م / ثانية2،
وهو التسارع الموازي لميل المنحدر عندما يكون هناك قوة احتكاك معاكسة مقدارها 45.0 نيوتن N.
الدلالة
نظرًا لأن الاحتكاك دائمًا ما يعارض الحركة بين الأسطح، فإن التسارع يكون أصغر عندما يكون هناك احتكاك منه عندما لا يكون هناك أي احتكاك. إنها نتيجة عامة أنه إذا كان الاحتكاك على منحدر ضئيلًا، فإن التسارع لأسفل المنحدر هو a = g sin θ، بغض النظر عن الكتلة. كما ناقشنا سابقًا، تسقط جميع الكائنات بنفس التسارع في حالة عدم وجود مقاومة للهواء. وبالمثل، فإن جميع الكائنات، بغض النظر عن الكتلة، تنزلق على منحدر خالي من الاحتكاك بنفس التسارع (إذا كانت الزاوية هي نفسها).
مكوّنات قوة الجاذبية على المنحدر
عندما يوضع جسم على منحدر يصنع زاوية θ مع الأفقي، تنقسم قوة الجاذبية المؤثرة على الجسم إلى مكوّنين: قوة تعمل بشكل عمودي على المستوى، wy، وقوة تعمل بالتوازي مع المستوى، wx (الشكل 5.23). عادةً ما تكون القوة العمودية N⃗ مساوية في المقدار ومعاكسة في الاتجاه للمكوِّن العمودي للوزن. تتسبب القوة التي تعمل بالتوازي مع المستوى، wx، في تسريع الجسم لأسفل المنحدر.
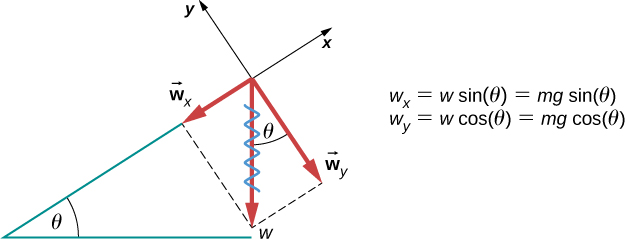
كن حذرًا عند تحليل وزن الكائن إلى مكوّنات x وy. إذا كان المنحدر يميل بزاوية θ على الأفقي، فإن مقادير مكونات الوزن تكون كما يلي:
wx = w sin θ = m g sin θ
وكذلك:
wy = w cos θ = m g cos θ
نستخدم المعادلة الثانية لكتابة القوة العادية التي يتعرض لها جسم يستقر على مستوى مائل:
N = m g cos θ
(5.13)
بدلاً من حفظ هذه المعادلات، من المفيد أن تكون قادرًا على تحديدها من خلال العقل. للقيام بذلك، نرسم الزاوية القائمة المكونة من متجهات الوزن الثلاثة. الزاوية θ لميل المنحدر هي نفس الزاوية المتكونة بين w و wy. بمعرفة هذه الخاصية، يمكننا استخدام علم المثلثات لتحديد مقدار مكوّنات الوزن:
cos θ =wy / w, wy = w cos θ = m g cos θ
sin θ = wx / w, wx = w sin θ = m g sin θ
تحقق من فهمك 5.8
تعمل قوة مقدارها 1150 نيوتن بالتوازي مع ميل منحدر لدفع خزنة وزنها 250 كجم في شاحنة متحركة. المنحدر عديم الاحتكاك ويميل بزاوية 17 درجة. (أ) ما هو تسارع الخزنة فوق المنحدر؟ (ب) إذا أخذنا في الاعتبار الاحتكاك في هذه المسألة بقوة احتكاك مقدارها 120 نيوتن، فما هو تسارع الخزنة؟
2. التوتر
التوتر Tension هو قوة تعمل على طول وسط معين، إنها قوة سحب تعمل على طول موصل مرن ممتد، مثل حبل أو كابل. تأتي كلمة “توتر” من كلمة لاتينية تعني “أن تتمدد” to stretch. ليس من قبيل الصدفة أن الحبال المرنة التي تحمل قوى العضلات إلى أجزاء أخرى من الجسم تسمى الأوتار.
أي موصل مرن، مثل خيط أو حبل أو سلسلة أو سلك أو كابل، يمكنه فقط ممارسة سحب موازٍ لطوله؛ وبالتالي، فإن القوة التي يحملها موصل مرن هي قوة توتر ذات اتجاه موازٍ للموصل. التوتر هو قوة سحب في الموصل. ضع في اعتبارك العبارة: “لا يمكنك دفع الحبل”. بدلاً من ذلك، يمكنك أن تسحب بقوة الشد للخارج على طول طرفي الحبل.
خذ بعين الاعتبار شخصًا يحمل كتلة على حبل، كما هو موضح في الشكل 5.24. إذا كانت الكتلة التي تبلغ 5.00 كجم في الشكل ثابتة، فإن تسارعها يساوي صفرًا والقوة الكلية أو محصلة القوى هي صفر. القوى الخارجية الوحيدة المؤثرة على الكتلة هي وزنها والتوتر الذي يوفره الحبل. وبالتالي يكون:
Fnet = T − w = 0
قانون حساب التوتر
حيث T وw هما مقدار التوتر (الشد) والوزن، على التوالي، وتشير إشاراتهما إلى الاتجاه، مع كون الاتجاه للأعلى موجبًا. كما أثبتنا باستخدام قانون نيوتن الثاني، فإن التوتر يساوي وزن الكتلة المرفوعة:
T = w = m g
(5.14)
وهكذا، بالنسبة لكتلة 5.00 كجم (مع إهمال كتلة الحبل)، فإنه يكون:
T = m g = (5.00kg) (9.80m / s2) = 49.0N
إذا قطعنا الحبل وأدخلنا زنبركًا، فإن الزنبرك سيتمدد بطول يقابل قوة مقدارها 49.0 نيوتن، مما يوفر ملاحظة وقياسًا مباشرًا لقوة الشد في الحبل.
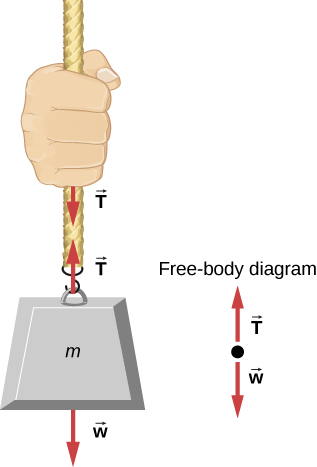
في الشكل 5.24: عندما ينقل موصل مرن تمامًا (لا يحتاج إلى قوة لثنيه) مثل هذا الحبل قوة T⃗، يجب أن تكون هذه القوة موازية لطول الحبل، كما هو موضح. بموجب قانون نيوتن الثالث، يشد الحبل بقوة متساوية ولكن في اتجاهين متعاكسين على كل من اليد والكتلة المرفوعة (مع إهمال وزن الحبل). الحبل هو الوسيط الذي يحمل القوى المتساوية والمتقابلة بين الجسمين. الشد في أي مكان في الحبل بين اليد والكتلة متساوي. بمجرد تحديد الشد في مكان واحد، تكون قد حددت الشد في جميع المواقع على طول الحبل.
أمثلة على قوى التوتر
غالبًا ما تُستخدم الموصلات المرنة لنقل القوى حول الزوايا، كما هو الحال في نظام الجر بالمستشفى أو الوتر أو كابل فرامل الدراجة. إذا لم يكن هناك احتكاك، فإن انتقال التوتر (الشد) يكون غير منقوص؛ يتغير اتجاهه فقط، ويكون دائمًا موازيًا للموصل المرن، كما هو موضح في الشكل 5.25.
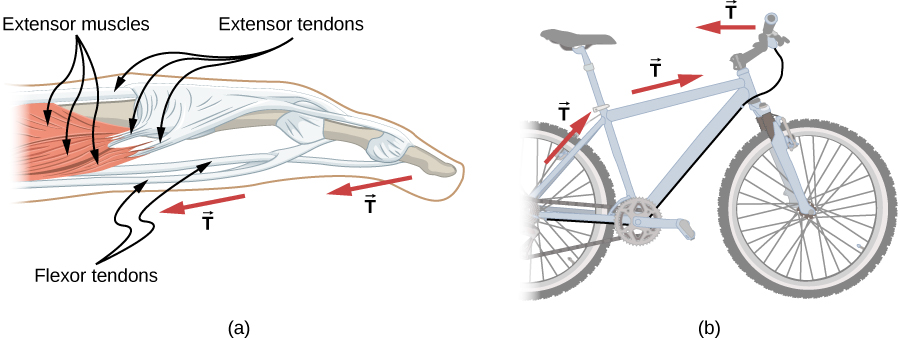
الشكل 5.25: (أ) تحمل الأوتار في الإصبع القوة T من العضلات إلى أجزاء أخرى من الإصبع، وعادةً ما تغير اتجاه القوة ولكن ليس مقدارها (الأوتار خالية نسبيًا من الاحتكاك). (ب) يحمل كيبل الفرامل على الدراجة التوتر T من ذراع المكابح على المقاود إلى آلية الفرامل. مرة أخرى، يتغير اتجاه T وليس مقدارها.
مثال 5.13: حساب التوتر في حبل مشدود
احسب الشد في السلك الذي يحمل الرجل الذي يمشي على الحبال والذي يبلغ وزنه 70.0 كجم كما هو موضح في الشكل 5.26.
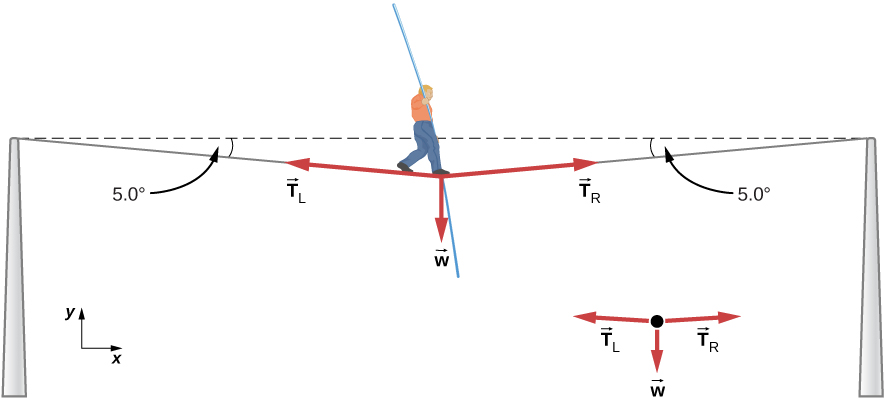
شكل 5.26: وزن الشخص الذي يمشي على حبل مشدود يتسبب في ترهل السلك بمقدار 5.0 درجة. نظام الاهتمام هو النقطة في السلك التي يقف عندها الشخص على الحبل المشدود.
استراتيجية الحل
كما ترى في الشكل 5.26، السلك مثني تحت وزن الشخص. وبالتالي، فإن التوتر على جانبي الشخص له مكوّن تصاعدي للأعلى يمكنه دعم وزنه. كالعادة، القوى هي نواقل ممثلة تصويريًا بأسهم لها نفس اتجاه القوى والأطوال المتناسبة مع مقاديرها. النظام هو الشخص الذي يمشي على الحبل المشدود، والقوى الخارجية الوحيدة التي تؤثر عليه هي وزنه مع التوترين T⃗L (التوتر الأيسر) و T⃗R (التوتر الأيمن). من المعقول إهمال وزن السلك. صافي القوة الخارجية هو صفر، لأن النظام ثابت (متزن). يمكننا استخدام حساب المثلثات لإيجاد التوترات. استنتاج واحد ممكن في البداية، يمكننا أن نرى من الشكل 5.26 (ب) أن مقادير التوترات TL و TR يجب أن تكون متساوية. نعلم هذا لأنه لا يوجد تسارع أفقي في الحبل والقوى الوحيدة المؤثرة على اليسار واليمين هما TL و TR. وبالتالي، يجب أن يكون مقدار تلك المكوّنات الأفقية للقوى متساويًا بحيث يلغي كل منهما الآخر.
عندما يكون لدينا مسائل متجه ثنائية الأبعاد لا يوجد فيها متجهان متوازيان، فإن أسهل طريقة للحل هي اختيار نظام إحداثيات مناسب وإسقاط المتجهات على محاورها. في هذه الحالة، يكون لأفضل نظام إحداثيات محور أفقي واحد (س) ومحور رأسي واحد (ص).
الحل
أولاً، نحتاج إلى تحليل متجهات الشد (التوتر) إلى مكوناتها الأفقية والرأسية. يساعد إلقاء نظرة على مخطط جديد للجسم الحر يوضح جميع المكونات الأفقية والرأسية لكل قوة تعمل على النظام (الشكل 5.27).
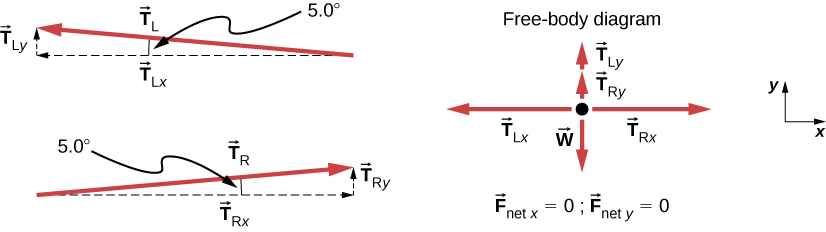
الشكل 5.27: عندما تُسقط المكونات المتجهة على محاور رأسية وأفقية، يجب أن يكون مجموع مكوناتها على طول هذه المحاور هو الصفر، نظرًا لأن جهاز المشي على الحبل المشدود ثابت. ينتج عن حقيقة أن الزاوية صغيرة أن T أكبر بكثير من w.
نفرض أن المكونات الأفقية للقوى (المشار إليها بالرمز x) كما يلي:
Fnetx = TRx − TLx.
صافي القوة الأفقية الخارجية Fnetx = 0، لأن الشخص ثابت. وهكذا يكون:
Fnetx = 0 = TRx – TLx
TLx = TRx
لاحظ الآن الشكل 5.27. يمكنك استخدام علم المثلثات لتحديد مقدار TL و TR:
cos 5.0 ° = TLx / TL , TLx = TL cos 5.0 °
cos 5.0 ° = TRx / TR , TRx = TR cos 5.0 °
بمساواة TLx و TRx، ينتج لنا:
TL cos 5.0° = TR cos 5.0°
وهكذا يكون:
TL = TR = T
حل المعادلة
كما كان متوقعا. الآن، بالنظر إلى المكوّنات الرأسية (المشار إليها بواسطة الرمز y)، يمكننا إيجاد T. مرة أخرى، نظرًا لأن الشخص ثابت، يشير قانون نيوتن الثاني إلى أن Fnety = 0. وهكذا، كما هو موضح في مخطط الجسم الحر:
Fnety = TLy + TRy − w = 0
يمكننا استخدام علم المثلثات لتحديد العلاقات بين TLy و TRy و T. كما حددنا من التحليل في الاتجاه الأفقي، TL = TR = T:
sin5.0 ° sin5.0 ° == TLyTL، TLy = TLsin5.0 ° = Tsin5.0 ° TRyTR، TRy = TRsin5.0 ° = Tsin5.0 °.
يمكننا الآن استبدال القيمتين لـ TLy و TRy، في معادلة القوة الصافية (المحصلة) في الاتجاه العمودي:
FnetyFnety2Tsin5.0 ° −w2Tsin5.0 ° ==== TLy + TRy − w = 0Tsin5.0 ° + Tsin5.0 ° −w = 00w
و
T = w2sin5.0 ° = mg2sin5.0 °
لذا يكون:
T=(70.0kg)(9.80m/s2)2(0.0872),T=(70.0kg)(9.80m/s2)2(0.0872),
أي أن التوتر يساوي:
T = 3930 N
الدلالة
يعمل التوتر الرأسي في السلك كقوة تدعم وزن الشخص الذي يمشي على الحبل المشدود. يبلغ الشد ستة أضعاف وزن الشخص (وزنه 686 نيوتن N). نظرًا لأن السلك أفقي تقريبًا، فإن المكوّن الرأسي لتوتره ليس سوى جزء بسيط من التوتر في السلك. المكوّنات الأفقية الكبيرة في الاتجاهين المتعاكسين تغلي بعضها، لذلك لا يتم استخدام معظم التوتر الأصلي في السلك لدعم (حمل) وزن الشخص الذي يمشي على الحبل المشدود.
إذا أردنا خلق توتر كبير، فكل ما علينا فعله هو بذل قوة عمودية على موصل مرن مشدود، كما هو موضح في الشكل 5.26. كما رأينا في المثال 5.13، فإن وزن الشخص الذي يمشي على الحبل المشدود يعمل كقوة عمودية على الحبل. رأينا أن الشد في الحبل مرتبط بوزن الشخص بالطريقة التالية:
T = w / 2 sin θ
يمكننا تمديد هذا التعبير لوصف التوتر T الناتج عند ممارسة قوة عمودية (F⊥) في منتصف موصل مرن:
T = F⊥ / 2 sin θ
تطبيقات في الحياة اليومية
يتم تمثيل الزاوية بين الموصل الأفقي والموصل المنحني بواسطة θ. في هذه الحالة، يصبح T كبيرًا عندما تقترب هذه الزاوية من الصفر. حتى الوزن الصغير نسبيًا لأي موصل مرن سيؤدي إلى ترهله، نظرًا لأن التوتر اللانهائي سينتج إذا كان أفقيًا (أي، θ = 0 وكذلك sin θ = 0). على سبيل المثال، يوضح الشكل 5.28 موقفًا نرغب فيه في سحب سيارة من الوحل عند عدم توفر شاحنة سحب. في كل مرة تتحرك فيها السيارة للأمام، يتم إحكام السلسلة لإبقائها مستقيمة قدر الإمكان. يُعطى التوتر في السلسلة بواسطة المعادلة T = F⊥ / 2 sin θ ، وبما أن θ صغيرة، فإن T كبيرة. هذا الموقف مشابه لمشي الرجل على الحبل المشدود، باستثناء أن التوترات الموضحة هنا هي تلك التي تنتقل إلى السيارة والشجرة بدلاً من تلك التي تعمل في النقطة التي يتم فيها تطبيق ⊥F.

الشكل 5.28: يمكننا أن نخلق توترًا كبيرًا في الحبل وبالتالي شدة كبيرة بالضغط عليه بشكل عمودي على طوله، كما هو موضح لتوفير الجهد.
تحقق من فهمك
أحد طرفي حبل طوله 3.0 م مربوط بشجرة. الطرف الآخر مربوط بسيارة عالقة في الوحل. يسحب سائق السيارة جانبًا على منتصف الحبل، ويزيحه مسافة 0.25 متر. إذا بذل قوة مقدارها 200.0 نيوتن (N) في ظل هذه الظروف، فأوجد القوة المؤثرة على السيارة.
في تطبيقات قوانين نيوتن، نوسع المناقشة حول التوتر في الكابل ليشمل الحالات التي تكون فيها الزوايا الموضحة في الشكل غير متساوية.
3. قوة الاحتكاك
قوة الاحتكاك هي قوة مقاومة معارضة للحركة أو معاكسة لاتجاهها. تخيّل جسمًا في حالة سكون على سطح أفقي. يجب أن تكون القوة الكلية المؤثرة على الجسم مساوية صفر، مما يؤدي إلى تساوي الوزن والقوة الطبيعية، اللذين يعملان في اتجاهين متعاكسين. إذا كان السطح مائلاً، فإن القوة الطبيعية تعمل على موازنة مكوّن الوزن في الاتجاه العمودي على السطح. إذا لم ينزلق الجسم لأسفل، فإن مكوّن الوزن الموازي للمستوى المائل يتوازن مع الاحتكاك. تمت مناقشة الاحتكاك بمزيد من التفصيل في الفصل التالي.
4. قوة الزنبرك (قانون هوك)
الزنبرك هو وسيط خاص له بنية ذرية محددة له القدرة على استعادة شكله، إذا كان مشوهًا أو منحنيًا. لاستعادة شكله، يمارس الزنبرك قوة استعادة تتناسب طرديًا مع وفي الاتجاه المعاكس للقوة التي يتم شده أو ضغطه بها. هذا هو بيان القانون المعروف باسم قانون هوك، والذي له الشكل الرياضي التالي:
F⃗ = − k x⃗
ثابت التناسب k هو مقياس صلابة الزنبرك. يكون خط عمل هذه القوة موازيًا لمحور الزنبرك، ويكون الإحساس بالقوة في الاتجاه المعاكس لمتجه الإزاحة (الشكل 5.29). يجب قياس الإزاحة من وضع الاسترخاء، حيث x = 0 عندما سترخي الزنبرك.
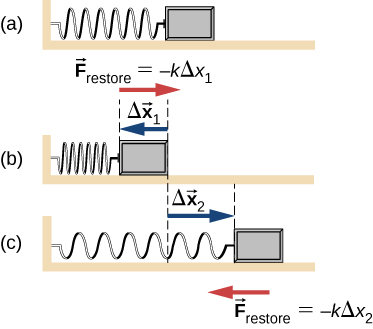
الشكل 5.29: يمارس الزنبرك قوته بالتناسب مع الإزاحة، سواء كان مضغوط أو مشدود. (أ) الزنبرك في وضع مريح ولا يمارس أي قوة على الكتلة. (ب) يتم ضغط الزنبرك عن طريق الإزاحة Δx⃗ 1 للجسم ويمارس قوة الاستعادة -kΔx⃗ 1. (ج) يتم شد الزنبرك عن طريق الإزاحة Δx⃗ 2 للجسم ويمارس قوة الاستعادة -kΔx⃗ 2.
القوى الحقيقية وإطارات القصور الذاتي
هناك فرق آخر بين القوى: بعض القوى حقيقية والبعض الآخر ليس كذلك. القوى الحقيقية لها أصل مادي، مثل قوة الجاذبية. في المقابل، تنشأ القوى الوهمية لمجرد أن المراقب في إطار مرجعي متسارع أو غير داخلي، مثل الذي يدور (مثل دوامة ألعاب الملاهي) أو يخضع لتسارع خطي (مثل سيارة تتباطأ). على سبيل المثال، إذا كان القمر الصناعي يتجه شمالًا فوق نصف الكرة الشمالي للأرض، فعندئذٍ، بالنسبة إلى مراقب على الأرض، سيبدو أنه يواجه قوة باتجاه الغرب ليس لها أصل مادي. بدلاً من ذلك، تدور الأرض باتجاه الشرق وتتحرك شرقًا تحت القمر الصناعي. في إطار الأرض، يبدو هذا كقوة باتجاه الغرب على القمر الصناعي، أو يمكن تفسيره على أنه انتهاك لقانون نيوتن الأول (قانون القصور الذاتي).
يمكننا تحديد القوة الوهمية من خلال طرح السؤال، “ما هي قوة رد الفعل؟” إذا لم نتمكن من تسمية قوة رد الفعل، فإن القوة التي نفكر فيها وهمية. في مثال القمر الصناعي، يجب أن تكون قوة رد الفعل هي قوة باتجاه الشرق على الأرض. تذكر أن الإطار المرجعي بالقصور الذاتي هو الإطار الذي تكون فيه جميع القوى حقيقية، وبشكل مكافئ، هو إطار يكون لقوانين نيوتن الأشكال البسيطة الواردة في هذا الفصل.
الإطارات بالقصور الذاتي
يكون دوران الأرض بطيئًا بدرجة كافية بحيث تكون الأرض عبارة عن إطار بالقصور الذاتي تقريبًا. يجب عادةً إجراء تجارب دقيقة لملاحظة القوى الوهمية والانحرافات الطفيفة عن قوانين نيوتن، مثل التأثير الموصوف للتو. وعلى نطاق واسع، يمكن ملاحظة التأثيرات بسهولة في أمثلة مثل دوران أنظمة الطقس وتيارات المحيطات (الشكل 5.30).

الشكل 5.30: إعصار فران يظهر متجهًا نحو الساحل الجنوبي الشرقي للولايات المتحدة في سبتمبر 1996. لاحظ شكل “العين” المميز للإعصار. هذا نتيجة لتأثير كوريوليس، وهو انحراف الأجسام (في هذه الحالة، الهواء) عند النظر إليه في إطار مرجعي دوار، مثل دوران الأرض. يُظهر هذا الإعصار دورانًا في عكس اتجاه عقارب الساعة لأنه عاصفة منخفضة الضغط. (المصدر: بواسطة “غرينتش فوتوغرافي” / فليكر).
العامل الحاسم في تحديد ما إذا كان الإطار المرجعي هو القصور الذاتي هو ما إذا كان يتسارع أو يدور بالنسبة إلى إطار بالقصور الذاتي المعروف. ما لم يذكر خلاف ذلك، نوقشت جميع الظواهر في هذا الكتاب في إطارات بالقصور الذاتي.
القوى التي نوقشت في هذا القسم هي قوى حقيقية، لكنها ليست القوى الحقيقية الوحيدة. الرفع والدفع، على سبيل المثال، قوى حقيقية أكثر تخصصًا. في القائمة الطويلة للقوى، هل بعضها أساسي أكثر من البعض الآخر؟ هل هناك بعض المظاهر المختلفة لنفس القوة الكامنة؟ الإجابة على كلا السؤالين هي نعم، كما سترى في معالجة الفيزياء الحديثة لاحقًا في هذا الكتاب.
تعليم تفاعلي
- استكشف القوى والحركة في هذه المحاكاة التفاعلية بينما تدفع الأشياء المنزلية لأعلى ولأسفل على منحدر. اخفض المنحدر وارفعه لترى كيف تؤثر زاوية الميل على القوى الموازية. تظهر الرسوم البيانية القوى والطاقة والشغل.
- قم بمد وضغط الينابيع في هذا النشاط لاستكشاف العلاقات بين القوة وثابت الزنبرك والإزاحة. تحقق مما يحدث عندما يتم توصيل زنبركين متصلين على التوالي في سلسلة أو على التوازي.
المراجع
- موسوعة الفيزياء العامة، ترجمة وإعداد: د. م. مصطفى عبيد، مركز البحوث والدراسات متعدد التخصصات، إسطنبول، 2022.
- كتاب الفيزياء للجامعات، صموئيل جيه لينغ، جامعة ولاية ترومان، د. جيف ساني، جامعة لويولا ماريماونت ويليام مويبس.