الشغل وطاقة الحركة
في هذا الفصل، نناقش بعض المفاهيم الفيزيائية الأساسية المتضمنة في كل حركة فيزيائية في الكون، ونتجاوز مفاهيم القوة والتغيير في الحركة، والتي ناقشناها في الحركة في بعدين وثلاثة أبعاد وقوانين نيوتن للحركة. هذه المفاهيم هي الشغل Work والطاقة الحركية Kinetic Energy والقوة. نشرح كيف ترتبط هذه الكميات ببعضها البعض، وهو ما سيقودنا إلى علاقة أساسية تسمى نظرية الشغل والطاقة. في الفصل التالي، سنعمم هذه الفكرة على المبدأ الأوسع للحفاظ على الطاقة.

صورة لستة متسابقين يصلون إلى خط نهاية السباق.
الشكل 7.1: تمارس العداءة أقصى قوتها بأكبر قوة في الوقت القصير الذي تلامس فيه قدمها الأرض. هذا يضيف إلى طاقتها الحركية، مما يمنعها من التباطؤ أثناء السباق. يولد الدفع بقوة على المسار قوة رد فعل تدفع العداء إلى الأمام للفوز في النهاية. (المصدر: ماري لان نغوين)
مخطط الفصل
- 7.1 الشغل
- 7.2 الطاقة الحركية
- 7.3 نظرية الشغل والطاقة
- 7.4 القدرة
المحتويات
عادة ما يتطلب تطبيق قوانين نيوتن حل المعادلات التفاضلية التي تربط القوى المؤثرة على جسم ما بالتسارع الذي ينتجه. غالبًا ما يكون الحل التحليلي صعبًا أو مستحيلًا، ويتطلب حلولًا رقمية طويلة أو عمليات محاكاة للحصول على نتائج تقريبية. في مثل هذه الحالات، يمكن للعلاقات الأكثر عمومية، مثل نظرية الشغل والطاقة (أو مبدأ الحفاظ على الطاقة)، أن تقدم إجابات مفيدة للعديد من الأسئلة وتتطلب قدرًا أكثر تواضعًا من الحسابات الرياضية. على وجه الخصوص، سترى كيف تكون نظرية الشغل والطاقة مفيدة في ربط سرعات الجسيم، في نقاط مختلفة على طول مساره، بالقوى المؤثرة عليه، حتى عندما يكون المسار معقدًا للغاية بحيث لا يمكن التعامل معه. وبالتالي، يمكن معالجة بعض جوانب الحركة بمعادلات أقل وبدون تحليل متجه.
الشغل
أهداف التعلم
بنهاية هذا القسم، ستكون قادرًا على:
- تمثيل الشغل الذي تقوم به أي قوة
- تقييم الشغل المنجز للقوى المختلفة
في الفيزياء، يتم الشغل على جسم ما عند نقل الطاقة إليه. بمعنى آخر، يتم الشغل عندما تعمل القوة على شيء ويخضع للإزاحة من موضع إلى آخر. يمكن أن تتنوع القوى كدالة للموضع، ويمكن أن تكون عمليات الإزاحة على طول مسارات مختلفة بين نقطتين. نحدد أولاً زيادة الشغل dW الذي تقوم به القوة F→ التي تؤثر من خلال إزاحة متناهية الصغر dr كناتج الضرب النقطي (القياسي) لهذين المتجهين كما يلي:
(7.1)
بعد ذلك، يمكننا جمع مساهمات عمليات الإزاحة المتناهية الصغر، على طول مسار بين موضعين، للحصول على إجمالي الشغل.
الشغل المبذول بواسطة قوة
الشغل الذي تقوم به القوة هو تكامل القوة فيما يتعلق بالإزاحة على طول مسار الإزاحة:
(7.2)
يوضح الشكل 7.2 المتجهات المتضمنة في تعريف الشغل الذي تقوم به القوة المؤثرة على الجسيم.
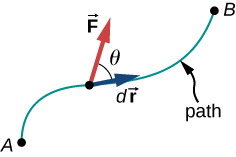
الشكل 7.2: المتجهات المستخدمة لتعريف الشغل. تظهر القوة المؤثرة على الجسيم وإزاحته المتناهية الصغر عند نقطة واحدة على طول المسار بين A وB. الشغل المتناهي الصغر هو حاصل الضرب النقطي لهذين المتجهين؛ إجمالي الشغل هو تكامل حاصل الضرب النقطي على طول المسار.
نختار التعبير عن حاصل الضرب النقطي (القياسي) من حيث مقادير المتجهات وجيب تمام الزاوية بينهما، لأن معنى حاصل الضرب القياسي للشغل يمكن أن يوضع في كلمات بشكل مباشر أكثر من حيث المقادير والزوايا. كان بإمكاننا أيضًا التعبير عن حاصل الضرب النقطي من حيث المكونات المختلفة المقدمة في المتجهات. في بعدين، كان هذان المكونان x و y في الإحداثيات الديكارتية، أو المكونات r و فاي في الإحداثيات القطبية؛ في ثلاثة أبعاد، كانت المكونات x و y و z فقط. الخيار الأكثر ملاءمة يعتمد على الموقف. بعبارة أخرى، يمكنك التعبير عن المعادلة 7.1 للشغل الذي تقوم به قوة مؤثرة على الإزاحة كحاصل ضرب أحد المكونات يعمل بالتوازي مع المكون الآخر. من خصائص المتجهات، لا يهم إذا أخذنا مكون القوة الموازي للإزاحة أو مكون الإزاحة الموازي للقوة، ستحصل على نفس النتيجة في كلتا الحالتين.
تذكر أن مقدار القوة مضروبًا في جيب تمام الزاوية التي تصنعها القوة في اتجاه معين هو مكون القوة في الاتجاه المحدد. يمكن أن تكون مكونات المتجه موجبة أو سالبة أو صفرية، اعتمادًا على ما إذا كانت الزاوية بين المتجه واتجاه المكون تقع بين 0° و 90°، أو 90° و 180°، أو تساوي 90°. نتيجة لذلك، يمكن أن يكون الشغل الذي تقوم به القوة موجبًا، أو سالبًا، أو صفرًا، اعتمادًا على ما إذا كانت القوة عمومًا في اتجاه الإزاحة، أو بشكل عام عكس الإزاحة، أو متعامدة مع الإزاحة.
أقصى شغل يتم بواسطة قوة معينة عندما تكون على طول اتجاه الإزاحة (Cos θ = ± 1)، ويتم شغل مقداره صفر عندما تكون القوة متعامدة مع الإزاحة (Cos θ = 0).
وحدات قياس الشغل هي وحدات قوة مضروبة في وحدات الطول، وهي في نظام SI نيوتن مضروبة في المتر N⋅m.
تسمى هذه المجموعة بالجول، لأسباب تاريخية سنذكرها لاحقًا، ويتم اختصارها كحرف J. في النظام الإنجليزي، الذي لا يزال مستخدمًا في الولايات المتحدة، وحدة القوة هي الباوند أو الرطل (lb) ووحدة المسافة هي القدم (قدم)، إذن وحدة الشغل هي قدم رطل (ft⋅lb).
الشغل المبذول من القوى الثابتة وقوى الاتصال
أبسط شغل يجب قياسه هو ذلك الذي تقوم به قوة ثابتة في المقدار والاتجاه. في هذه الحالة، يمكننا تحليل القوة؛ التكامل المتبقي هو مجرد الإزاحة الكلية، والتي تعتمد فقط على نقطتي النهاية A وB، ولكن ليس على المسار بينهما:
يمكننا أيضًا ملاحظة ذلك من خلال كتابة المعادلة 7.2 بالإحداثيات الديكارتية واستخدام حقيقة أن مكونات القوة ثابتة:
يوضح الشكل 7.3 (أ) شخصًا يمارس قوة ثابتة F→ على طول مقبض جزازة العشب، والتي تصنع زاوية θ مع الأفقي. الإزاحة الأفقية لجزازة العشب، والتي تعمل القوة عليها، هي d→.
الشغل المبذول على جزازة العشب هو:
والذي يوضحه الشكل أيضًا على أنه المكون الأفقي للقوة مضروبًا في مقدار الإزاحة.
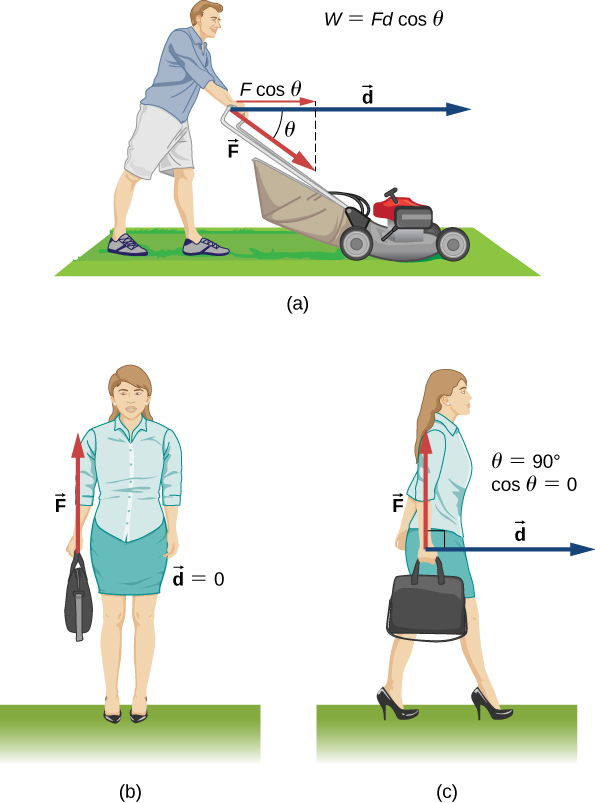
الشكل 7.3: الشغل الذي تقوم به قوة ثابتة. (أ) يدفع شخص جزازة العشب بقوة ثابتة. مكون القوة الموازية للإزاحة هو الشغل المبذول، كما هو موضح في المعادلة في الشكل. (ب) شخص يحمل حقيبة. لم يتم القيام بأي عمل لأن الإزاحة تساوي صفرًا. (ج) يمشي الشخص الموجود في (ب) أفقيًا وهو يحمل الحقيبة. لم يتم إنجاز أي عمل بسبب أن Cos θ = 0 هو صفر.
يوضح الشكل 7.3 (ب) شخصًا يحمل حقيبة. يجب على الشخص أن يبذل قوة صاعدة تساوي وزن الحقيبة، لكن هذه القوة لا تبذل شغل، لأن الإزاحة التي تعمل عليها تساوي صفرًا.
في الشكل 7.3 (ج)، حيث يسير الشخص الموجود في (ب) أفقيًا بسرعة ثابتة، فإن الشغل الذي قام به الشخص الموجود على الحقيبة لا يزال صفرًا، ولكن الآن لأن الزاوية بين القوة المبذولة والإزاحة هي 90° ( F→ عمودية على d→) وCos θ = 0 .
مثال 7.1: حساب الشغل الذي تقوم به لدفع جزازة العشب
ما مقدار الشغل الذي يقوم به الشخص الموضح في الشكل 7.3 (أ) على جزازة العشب إذا بذل قوة ثابتة مقدارها 75 نيوتن بزاوية 35° تحت الأفقي ودفع الجزازة مسافة 25 متر على أرض مستوية؟
استراتيجية الحل
يمكننا حل هذه المسألة عن طريق استبدال القيم المعطاة في تعريف الشغل المبذول على كائن بقوة ثابتة، كما هو مذكور في المعادلة: W=Fdcosθ، يتم إعطاء القوة والزاوية والإزاحة، بحيث يكون الشغل W فقط غير معروف.
الحل
معادلة الشغل هي:
بالتعويض عن القيم المعروفة:
الدلالة
على الرغم من أن كيلو جول ونصف قد يبدو وكأنه يتطلب الكثير من الشغل، إلا أننا سنرى في موضوع الطاقة الكامنة وقانون حفظ الطاقة أنه يتعلق فقط بنفس القدر من الشغل الذي يمكنك القيام به عن طريق حرق سُدس جرام من الدهون.
تحليل القوى المؤثرة
عندما تقوم بقص العشب، تعمل قوى أخرى على جزازة العشب بالإضافة إلى القوة التي تمارسها – أي قوة التلامس مع الأرض وقوة الجاذبية الأرضية. دعونا ننظر في الشغل الذي قامت به هذه القوى بشكل عام. بالنسبة لجسم يتحرك على سطح، الإزاحة dr→ مماسة على السطح. الجزء المتعامد مع السطح من قوة التلامس على الجسم هو القوة الطبيعية N بما أن جيب تمام الزاوية بين العمودي والمماس لسطح ما يساوي صفرًا، فلدينا:
القوة الطبيعية لا تعمل أبدًا في ظل هذه الظروف. (لاحظ أنه إذا كانت الإزاحة dr⃗ تحتوي على مكون نسبي عمودي على السطح، فإن الكائن إما أن يترك السطح أو يخترقه، ولن يكون هناك أي قوة اتصال عادية. ومع ذلك، إذا كان الكائن أكثر من مجرد جسيم، وله بنية داخلية، يمكن لقوة الاتصال العادية أن تعمل عليه، على سبيل المثال، عن طريق إزاحته أو تشويه شكله. سيتم ذكر ذلك في الفصل التالي).
جزء قوة التلامس على الجسم الموازي للسطح هو الاحتكاك، F⃗. لهذا الجسم الذي ينزلق على طول السطح، الاحتكاك الحركي Fk هو عكس dr⃗. بالنسبة للسطح، فإن الشغل المبذول بواسطة الاحتكاك الحركي يكون سالبًا. إذا كان مقدار Fk ثابت (كما لو كانت جميع القوى الأخرى على الجسم ثابتة)، فإن الشغل المبذول بواسطة الاحتكاك هو:
(7.3)
حيث |lAB| هو طول المسار على السطح. لا تعمل قوة الاحتكاك الساكن في الإطار المرجعي بين سطحين لأنه لا يوجد إزاحة أبدًا بين السطحين. كقوة خارجية، يمكن للاحتكاك الساكن القيام بشغل. يمكن للاحتكاك الساكن أن يمنع أي شخص من الانزلاق عن الزلاجة عندما تتحرك المزلجة ويؤدي عملاً إيجابيًا على الشخص. إذا كنت تقود سيارتك عند الحد الأقصى للسرعة على امتداد مستقيم ومستوى للطريق السريع، فإن الشغل السلبي الذي تقوم به مقاومة الهواء يتم موازنته من خلال الشغل الإيجابي الذي يقوم به الاحتكاك الساكن للطريق على عجلات القيادة. يمكنك سحب السجادة من تحت أي شيء بطريقة تنزلق للخلف بالنسبة للسجادة، ولكن للأمام بالنسبة للأرضية. في هذه الحالة، يمكن أن يكون الاحتكاك الحركي الذي تمارسه السجادة على الجسم في نفس اتجاه إزاحة الجسم، بالنسبة إلى الأرضية، والقيام بشغل إيجابي. خلاصة القول هي أنك تحتاج إلى تحليل كل حالة معينة لتحديد الشغل الذي تقوم به القوى، سواء كانت إيجابية أو سلبية أو صفرية.
مثال 7.2: تحريك الأريكة
قررت نقل أريكتك إلى موضع جديد على أرضية غرفة المعيشة الأفقية. القوة العمودية المؤثرة على الأريكة تساوي 1 كيلو نيوتن ومعامل الاحتكاك 0.6. (أ) عليك أولاً دفع الأريكة 3 أمتار موازية للحائط ثم 1 متر عموديًا على الحائط (من أ إلى ب في الشكل 7.4 ). ما مقدار الشغل الذي تقوم به قوة الاحتكاك؟ (ب) لا يعجبك الوضع الجديد، لذلك تقوم بتحريك الأريكة مباشرة إلى موضعها الأصلي (من B إلى A في الشكل 7.4 ). ما هو إجمالي الشغل المبذول ضد الاحتكاك بتحريك الأريكة بعيدًا عن وضعها الأصلي وإعادتها مرة أخرى؟
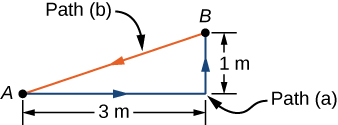
الشكل 7.4: منظر علوي لمسارات تحريك الأريكة
استراتيجية الحل
مقدار قوة الاحتكاك الحركي على الأريكة ثابت، يساوي معامل الاحتكاك مضروبًا في القوة العمودية، fK = μK N. لذلك، فإن الشغل الذي قام به هو Wfr = −fK d. حيث d هو طول المسار المقطوع. مقاطع المسارات هي جوانب المثلث القائم الزاوية، لذا يمكن حساب أطوال المسار بسهولة. في الجزء (ب)، يمكنك استخدام حقيقة أن الشغل المبذول ضد قوة هو السالب للشغل الذي تقوم به القوة.
الحل
(أ) الشغل الذي أنجزه الاحتكاك i:
(ب) طول المسار على طول الوتر هو 10√ متر، لذا فإن إجمالي الشغل المبذول ضد الاحتكاك هو:
الدلالة
بدأ المسار الإجمالي الذي تم من خلاله تقييم عمل الاحتكاك وانتهى عند نفس النقطة (كان مسارًا مغلقًا)، بحيث كان إجمالي إزاحة الأريكة صفرًا. ومع ذلك، فإن إجمالي الشغل لم يكن صفرًا. والسبب هو أن قوى مثل الاحتكاك تصنف على أنها قوى غير محافظة، أو قوى تبديد، كما نناقش في الفصل التالي.
تحقق من فهمك 7.1
هل يمكن أن يكون الاحتكاك الحركي قوة ثابتة لجميع المسارات؟
الشغل المبذول بواسطة الجاذبية
القوة الأخرى على جزازة العشب المذكورة أعلاه هي قوة الجاذبية الأرضية، أو وزن الجزازة. بالقرب من سطح الأرض، قوة الجاذبية على جسم كتلته m لها مقدار ثابت، mg، واتجاه ثابت، عموديًا لأسفل. إذن، الشغل المبذول بواسطة الجاذبية على جسم ما هو حاصل الضرب القياسي لوزنه وإزاحته.
في كثير من الحالات، يكون من الملائم التعبير عن حاصل الضرب القياسي أو النقطي لشغل الجاذبية بدلالة مكونات x و y و z للمتجهات. يحتوي نظام الإحداثيات النموذجي على المحور السيني أفقيًا والمحور الصادي عموديًا. ثم تكون قوة الجاذبية mgjˆ، لذا فإن الشغل المبذول عن طريق الجاذبية، على أي مسار من أ إلى ب، هو:
(7.4)
الشغل الذي تقوم به قوة الجاذبية الثابتة على جسم ما يعتمد فقط على وزن الجسم والاختلاف في الارتفاع الذي يتم من خلاله إزاحة الجسم. تقوم الجاذبية يشغل سالب على جسم يتحرك لأعلى (yB>yA)، أو بعبارة أخرى، يجب عليك القيام بعمل إيجابي ضد الجاذبية لرفع الجسم لأعلى. وبالعكس، تقوم الجاذبية بشغل إيجابي على جسم يتحرك لأسفل (yB<yA)، أو تقوم بشغل سلبي ضد الجاذبية من أجل “رفع” الجسم لأسفل، والتحكم في هبوطه حتى لا يسقط على الأرض. (يتم استخدام “Lift” بدلاً من “drop”).
مثال 7.3: رفع كتاب إلى الرف
يمكنك رفع كتاب مكتبة كبير الحجم، يزن 20 نيوتن، متر واحد رأسيًا لأسفل من الرف، وتحمله 3 أمتار أفقيًا إلى طاولة ( الشكل 7.5 ). ما مقدار الشغل الذي تقوم به الجاذبية على الكتاب؟ (ب) عند الانتهاء، تقوم بنقل الكتاب في خط مستقيم إلى مكانه الأصلي على الرف. ما هو إجمالي الشغل الذي تم القيام به ضد الجاذبية، لنقل الكتاب بعيدًا عن موضعه الأصلي على الرف وإعادته مرة أخرى؟
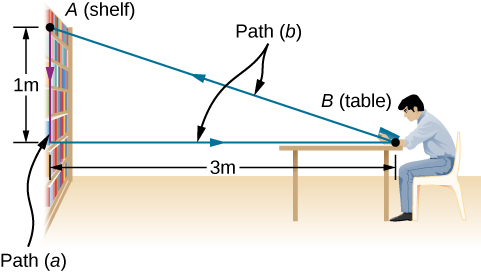
الشكل 7.5: منظر جانبي لمسارات نقل الكتاب من الرف وإليه.
استراتيجية الحل
لقد رأينا للتو أن الشغل الذي تقوم به قوة الجاذبية الثابتة يعتمد فقط على وزن الجسم المتحرك والفرق في الارتفاع للمسار المتخذ، WAB=−mg(yB−yA). يمكننا حساب الفرق في الارتفاع للإجابة على (أ) و (ب).
الحل
(أ) لأن الكتاب يبدأ على الرف ويرفع للأسفل، يكون:
yB − yA = − 1 m
لدينا:
(ب) لا يوجد فرق في الارتفاع لأي مسار يبدأ وينتهي في نفس المكان على الرف، لذلك فإن الشغل W=0.
الدلالة
تقوم الجاذبية بعمل إيجابي (20 J) عندما يتحرك الكتاب لأسفل من الرف. قوة الجاذبية بين جسمين هي قوة جاذبة، تقوم بعمل إيجابي عندما يقترب الجسمان من بعضهما البعض. الجاذبية تبذل شغل مقداره صفرًا (0 J) عندما يتحرك الكتاب أفقيًا من الرف إلى الطاولة وتبذل شغل سلبي (−20 J) عندما ينتقل الكتاب من الطاولة إلى الرف. إجمالي الشغل الذي تقوم به الجاذبية هو صفر [20جول + 0 جول + (- 20 جول) = صفر].
على عكس الاحتكاك أو قوى التبديد الأخرى، الموصوفة في المثال 7.2، فإن إجمالي الشغل المبذول ضد الجاذبية، على أي مسار مغلق، هو صفر. يتم عمل الشغل الموجب ضد الجاذبية على الأجزاء الصاعدة من مسار مغلق، لكن قدرًا متساويًا من الشغل السالب يتم مقابل الجاذبية على الأجزاء الهابطة. بعبارة أخرى، العمل ضد الجاذبية، ورفع الجسم للأعلى، “يُعاد” عندما يعود الجسم إلى الأسفل. تُصنف قوى مثل الجاذبية (تلك التي لا تبذل شغل مقداره صفر على أي مسار مغلق) على أنها قوى محافظة وتلعب دورًا مهمًا في الفيزياء.
تحقق من فهمك 7.2
هل يمكن أن تكون جاذبية الأرض قوة ثابتة لجميع المسارات؟
الشغل المبذول بواسطة قوى متغيرة
بشكل عام، قد تتغير القوى من حيث الحجم والاتجاه عند نقاط في الفضاء، وقد تكون المسارات بين نقطتين منحنية. يمكن التعبير عن الشغل المتناهي الصغر الذي تقوم به قوة متغيرة من حيث مكونات القوة والإزاحة على طول المسار كما يلي:
هنا، مكونات القوة هي دوال الموضع على طول المسار، وتعتمد الإزاحات على معادلات المسار. (على الرغم من أننا اخترنا توضيح dW في الإحداثيات الديكارتية، إلا أن الإحداثيات الأخرى مناسبة بشكل أفضل لبعض المواقف).
تُعرِّف المعادلة 7.2 إجمالي الشغل باعتباره التكامل الخطي، أو نهاية مجموع كميات الشغل المتناهية الصغر. المفهوم المادي للشغل واضح ومباشر: فأنت تحسب الشغل لحالات النزوح الصغيرة وتجمعها. في بعض الأحيان، قد تبدو الرياضيات معقدة، لكن المثال التالي يوضح كيف يمكن أن تعمل بطريقة نظيفة.
مثال 7.4: الشغل المبذول بواسطة قوة متغيرة على مسار منحنٍ
كائن يتحرك على طول مسار قطع مكافئ: y=(0.5m−1)x2
من نقطة الأصل A(0.0)، الى النقطة B(2m.2m)، تحت تأثير القوة:
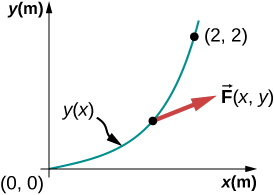
الشكل 7.6: المسار المكافئ لجسيم يتأثر بقوة معينة.
استراتيجية الحل
تُعطى مكونات القوة دالات x و y. يمكننا استخدام معادلة المسار للتعبير عن y و dy بدلالة x و dx؛ أي:
إذن، فإن تكامل الشغل هو مجرد تكامل نهاية لدالة في المتغير x.
الحل
عنصر الشغل متناهي الصغر هو:
تكامل x2 هو x3/3، لذا يكون:
الدلالة
هذا التكامل لم يكن صعبًا. يمكنك اتباع نفس الخطوات، كما في هذا المثال ، لحساب التكاملات الخطية التي تمثل الشغل لقوى ومسارات أكثر تعقيدًا. في هذا المثال، تم إعطاء كل شيء بدلالة مكونات x و y وهي أسهل استخدامًا في حساب الشغل في هذه الحالة. في حالات أخرى، قد تكون المقادير والزوايا أسهل.
تحقق من فهمك 7.3
أوجد الشغل الذي تقوم به نفس القوة في مثال 7.4 على مسار تكعيبي: y=(0.25m−2)x3، بين نفس النقاط A(0,0) وB(2,2).
الشغل المبذول بواسطة الزنبرك
لقد رأيت في المثال 7.4 أنه لحساب تكامل خطي، يمكنك اختزاله إلى تكامل عبر متغير أو معلمة واحدة. عادة، هناك عدة طرق للقيام بذلك، والتي قد تكون أكثر أو أقل ملاءمة، حسب الحالة المعينة. في المثال 7.4، قمنا باختصار التكامل الخطي إلى تكامل على x، لكن يمكننا أيضًا اختيار اختزال كل شيء إلى دالة y. لم نفعل ذلك لأن الدوال في y تتضمن الجذر التربيعي والأسس الكسرية، والتي قد تكون أقل شيوعًا، ولكن لأغراض توضيحية، نقوم بذلك الآن. نحصل على قيمة x وdx بدلالة y على طول المسار المكافئ، نحصل على:
مكونات القوة، بدلالة y، هي:
لذلك يصبح عنصر الشغل المتناهي الصغر هو:
تكامل y1/2 هو 2/3 y3/2، لذا فإن الشغل المبذول من أ إلى ب هو:
كما هو متوقع، هذه هي النتيجة نفسها تمامًا كما كان من قبل.
إحدى القوى المتغيرة المهمة جدًا والقابلة للتطبيق على نطاق واسع هي القوة التي يمارسها زنبرك مرن تمامًا، والذي يتوافق مع قانون هوك:
حيث k هو ثابت الزنبرك، و dx = x − xeq
هي الإزاحة من وضع الزنبرك غير الممتد (التوازن) (قوانين نيوتن للحركة). لاحظ أن الوضع غير الممدود هو فقط نفس وضع التوازن إذا لم تكن هناك قوى أخرى تعمل (أو، إذا كانت كذلك، فإنها تلغي بعضها البعض). تتصرف القوى بين الجزيئات، أو في أي نظام يخضع لعمليات إزاحة صغيرة من توازن مستقر، تقريبًا مثل قوة الزنبرك.
لحساب الشغل الذي تقوم به قوة زنبركية، يمكننا اختيار المحور السيني على طول الزنبرك، في اتجاه زيادة الطول، كما في الشكل 7.7، حيث يكون الأصل في موضع التوازن xeq = صفر. (ثم يقابل x الموجبة الامتداد وx السالبة للضغط). مع اختيار الإحداثيات هذا، يكون لقوة الزنبرك مكون x فقط، حيث Fx=-k x. والشغل المبذول عندما تغير XA إلى XB يكون:
(7.5)
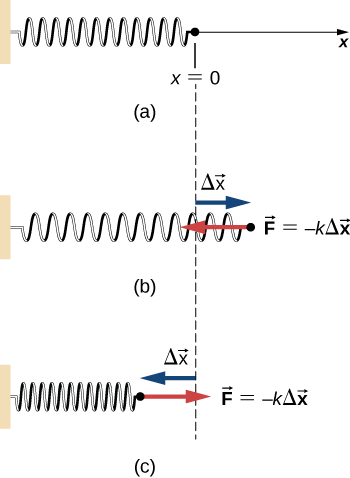
الشكل 7.7: (أ) لا يمارس الزنبرك أي قوة في موضع توازنه. يبذل الزنبرك قوة في الاتجاه المعاكس لـ (ب) امتداد أو تمدد، و (ج) ضغط.
لاحظ أن WAB يعتمد فقط على نقطتي البداية والنهاية، A وB، وهو مستقل عن المسار الفعلي بينهما، طالما أنه يبدأ من A وينتهي عند B. أي أن المسار الفعلي قد يتضمن الانتقال ذهابًا وإيابًا قبل النهاية.
شيء آخر مثير للاهتمام يجب ملاحظته بشأن المعادلة 7.5 هو أنه، في هذه الحالة أحادية البعد، يمكنك بسهولة رؤية التطابق بين الشغل الذي تقوم به القوة والمساحة الواقعة أسفل منحنى القوة مقابل إزاحتها. تذكر أنه، بشكل عام، التكامل أحادي البعد هو نهاية مجموع اللامتناهيات في الصغر f(x)dx، تمثل مساحة الشرائط، كما هو موضح في الشكل 7.8.
في المعادلة 7.5، حيث أن F=−kx هو خط مستقيم مع ميل -k، عند رسمها مقابل x، فإن “المنطقة” الموجودة أسفل الخط هي مجرد مجموعة جبرية من “المناطق” المثلثة، حيث تكون “المناطق” فوق المحور x موجبة وتلك الموجودة أدناه سالبة، كما هو موضح في الشكل 7.9. مقدار إحدى هذه “المناطق” هو فقط نصف قاعدة المثلث، على طول المحور x، مضروبًا في ارتفاع المثلث، على طول محور القوة. (توجد علامات اقتباس حول “المنطقة” لأن حاصل ضرب الارتفاع في القاعدة هذا يحتوي على وحدات الشغل بدلاً من المتر المربع).
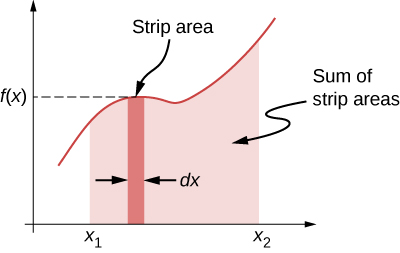
الشكل 7.8: منحنى f (x) مقابل x يوضح مساحة الشريط اللامتناهي، f(x) dx، ومجموع هذه المناطق، وهو تكامل f(x) من x1 إلى x2.
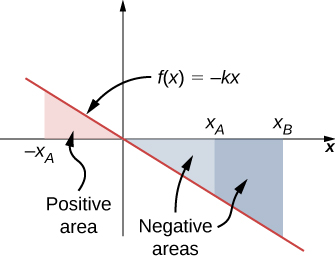
شكل 7.9: منحنى قوة الزنبرك f(x)=−kx مقابل x، إظهار المناطق الواقعة تحت الخط، بين xAوxB، لكل من القيم الموجبة والسالبة لـ xA. عندما تكون xA سالبة، المساحة الكلية تحت المنحنى للتكامل في المعادلة 7.5 هي مجموع مساحات المثلثات الموجبة والسالبة. حيث xA موجبة، المساحة الكلية تحت المنحنى هي الفرق بين مثلثين سالبين.
مثال 7.5: الشغل المبذول بواسطة قوة الزنبرك
يتطلب الزنبرك المرن تمامًا 0.54 جول من الشغل ليمتد بمقدار 6 سم من موضع توازنه، كما في الشكل 7.7 (ب). (أ) ما هو ثابت الزنبرك k؟ (ب) ما مقدار الشغل المطلوب لمده بمقدار 6 سم إضافية؟
استراتيجية الحل
الشغل “مطلوب” يعني الشغل المبذول ضد قوة الزنبرك، وهي الشغل السالب في المعادلة 7.5، أي:
للجزء (A)، xA=0 و xB=6 cm، للجزء (B)،xA=6cm و xB=12cm. في الجزء (A)، يتم إعطاء الشغل ويمكنك إيجاد ثابت الزنبرك؛ في الجزء (B)، يمكنك استخدام قيمة k، من الجزء (A)، للحل وإيجاد الشغل.
الحل
(أ)
(ب)
الدلالة
نظرًا لأن الشغل الذي تقوم به قوة الزنبرك مستقل عن المسار، ما عليك سوى حساب الفرق في الكمية 1/2kx2، في نقاط النهاية. لاحظ أن الشغل المطلوب لمد الزنبرك من 0 إلى 12 سم هو أربعة أضعاف ما يتطلبه شد الزنبرك من 0 إلى 6 سم، لأن هذا العمل يعتمد على مربع مقدار التمدد من الاتزان، 1/2kx2. في هذه الحالة، فإن العمل على مد الزنبرك من 0 إلى 12 سم يساوي أيضًا الشغل الخاص بمسار مركب من 0 إلى 6 سم متبوعًا بامتداد إضافي من 6 سم إلى 12 سم. لذلك:
أو:
كما وجدنا أعلاه.
تحقق من فهمك 7.4
يتم ضغط الزنبرك في المثال 7.5 بمقدار 6 سم من طول توازنه. (أ) هل تقوم قوة الزنبرك ببذل شغل موجب أم سالب و(ب) ما هو مقداره؟
المراجع
- موسوعة الفيزياء العامة، ترجمة وإعداد: د. م. مصطفى عبيد، مركز البحوث والدراسات متعدد التخصصات، إسطنبول، 2022.
- كتاب الفيزياء للجامعات، صموئيل جيه لينغ، جامعة ولاية ترومان، د. جيف ساني، جامعة لويولا ماريماونت ويليام مويبس.