قانون نيوتن الثاني
يرتبط قانون نيوتن الثاني ارتباطًا وثيقًا بقانونه الأول. وهو يعطي رياضيًا العلاقات بين السبب والنتيجة. قانون نيوتن الثاني هو قانون كمي ويستخدم على نطاق واسع لحساب ما يحدث في الحالات التي يوجد فيها قوة مؤثرة. قبل أن نتمكن من كتابة قانون نيوتن الثاني كمعادلة رياضية بسيطة تعطي العلاقة الدقيقة بين القوة والكتلة والتسارع، نحتاج إلى شحذ بعض الأفكار التي ذكرناها سابقًا.
أهداف التعلم:
بحلول نهاية هذا القسم ستكون قادرًا على:
- التمييز بين القوى الخارجية والداخلية والعلاقة بين القوة والتسارع والكتلة
- وصف قانون نيوتن الثاني واستخداماته وتطبيقاته العملية بالأمثلة
- شرح اعتماد التسارع على القوة المحصلة (صافي القوى) والكتلة
- فهم قانون نيوتن الثاني وزخم الحركة
المحتويات
العلاقة بين القوة والتسارع والكتلة
أولاً، ماذا نعني بالتغير في الحركة؟ الجواب هو أن التغير في الحركة يعادل التغيير في السرعة.
التغيير في السرعة يعني، بحكم التعريف، أنه تسارع. يقول قانون نيوتن الأول أن القوة الخارجية الصافية تسبب تغير في الحركة؛ وبالتالي، نرى قوة خارجية صافية تسبب تسارع غير صفري.
لقد عرّفنا القوة الخارجية في القسم السابق حول مفهوم القوى، على أنها قوة تؤثر على جسم أو نظام وتنشأ من خارج هذا الجسم أو النظام، أي ليس من داخله. لننظر في هذا المفهوم بشكل أكبر. فكرة بديهية لتبسيط مفهوم التأثير من الخارج، على سبيل المثال، في الشكل 5.10 (a)، فإن النظام محل البحث هو السيارة والشخص الذي يركب داخلها. القوتان المثارتان من قبل الشخصين الذين يدفعان السيارة هما القوى الخارجية. في المقابل، تعمل القوى الداخلية بين عناصر النظام. وبالتالي، فإن القوة التي يضغط بها سائق السيارة على مقود السيارة هي قوة داخلية نشأت بين عناصر النظام الداخلية. وفقط القوى الخارجية هي التي تؤثر على حركة النظام، وفقا لقانون نيوتن الأول. (تقوم القوى الداخلية بإلغاء كل منها للآخر، كما هو موضح في الفقرات التالية).
في بعض الأحيان، يكون النظام واضحًا، بينما في أحين أخرى، يكون تحديد حدود النظام أكثر دقة. مفهوم النظام أساسي للعديد من مجالات الفيزياء، من أجل التطبيق الصحيح لقوانين نيوتن. يتم إعادة النظر في هذا المفهوم عدة مرات أثناء دراسة الفيزياء.
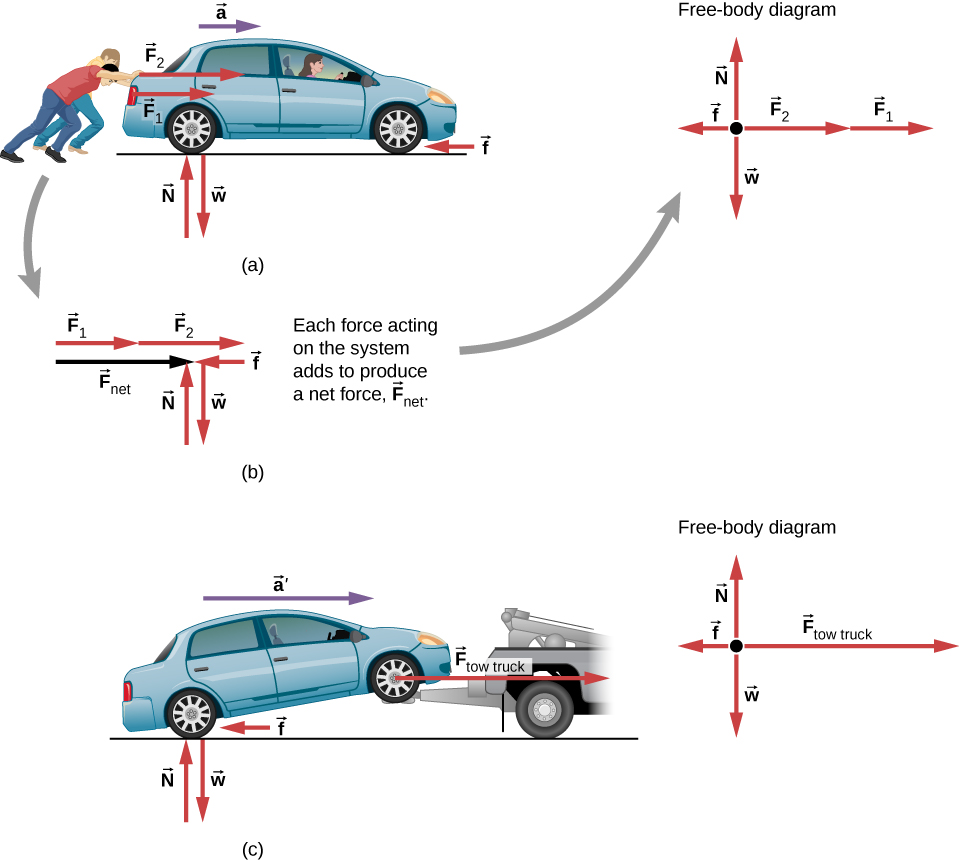
الشكل 5.10: قوى مختلفة تمارس على نفس الكتلة تنتج تسارعًا مختلفًا. (a) يدفع طالبان سيارة متوقفة. يتم عرض جميع القوى الخارجية التي تعمل على السيارة. (b) يتم نقل القوى التي تعمل على السيارة إلى مستوى إحداثيات (مخطط للجسم الحر) لتحليل أبسط. (c) يمكن لشاحنة السحب أن تنتج قوة خارجية أكبر على نفس الكتلة، وبالتالي تسارع أكبر.
القوى الداخلية والخارجية المؤثرة على جسم
من هذا المثال، يمكنك أن ترى أن القوى المختلفة التي تؤثر على نفس الكتلة تنتج تسارعًا مختلفًا. في الشكل 5.10 (a)، يدفع الطالبان سيارة مع سائق موجود بداخلها. وتظهر الأسهم التي تمثل جميع القوى الخارجية. نظام الاهتمام هو السيارة وسائقها. يتم عرض الوزن w⃗ للنظام ودفع الأرض N⃗ المعاكس للوزن لتكملة القوى جميعها (ويُفترض هنا أنهما يلغيان بعضهما البعض لأنه لم تكن هناك حركة عمودية ولا يوجد فرق في القوى في الاتجاه الرأسي لإنشاء تغيير في الحركة). يمثل المتجه f⃗ الاحتكاك الذي يؤثر على السيارة، ويعمل في اتجاه اليسار، ويعارض حركة السيارة. (سوف نناقش الاحتكاك بمزيد من التفصيل في الفصل التالي).
في الشكل 5.10 (b)، تضيف جميع القوى الخارجية التي تؤثر على النظام معًا لإنتاج محصلة القوى F⃗ net. يوضح مخطط الجسم الحر جميع القوى التي تعمل على النظام محل البحث. تمثل النقطة مركز كتلة النظام. يتم رسم كل متجه قوة من هذا النقطة. نظرًا لوجود قوتان تؤثران باتجاه اليمين، يتم عرض المتجهات الخاصة بها بشكل متتالي على نفس الخط. أخيرًا، في الشكل 5.10 (c)، تنتج قوة خارجية صافية أكبر تسارعًا أكبر وذلك عندما تسحب الشاحنة السحب السيارة:
a’ > a
العلاقة بين القوة والتسارع
يبدو من المعقول أن يكون التسارع يتناسب بشكل مباشر طرديًا مع القوة الخارجية الصافية، ويكون اتجاه التسارع في نفس الاتجاه الذي تؤثر فيه القوة على النظام. تم التحقق من هذا الافتراض تجريبيًا ويوضح ذلك الشكل 5.10.
للحصول على معادلة قانون نيوتن الثاني، نكتب أولاً العلاقة بين التسارع a⃗ ومحصلة القوى الصافية F⃗ net باعتبارها علاقة تناسب طردي:
a⃗ ∝ F⃗ net
حيث يعني الرمز ∝ “يتناسب طرديًا مع”. صافي القوى أو القوة الخارجية الصافية أو محصلة القوى هي المجموع الاتجاهي لجميع القوى الخارجية ويتم الإشارة إليها أحيانًا على أنها Σ F⃗ (وتُقرأ: سيجما).
بمجرد اختيار النظام محل البحث، حدد القوى الخارجية وتجاهل القوى الداخلية. إنه تبسيط هائل لتجاهل القوى الداخلية العديدة التي تعمل بين الأشياء داخل النظام، مثل القوى العضلية داخل أجسام الطلاب، ناهيك عن القوى التي لا تعد ولا تحصى بين الذرات في الأشياء. ومع ذلك، يساعدنا هذا التبسيط في حل بعض المسائل المعقدة.
العلاقة بين التسارع والكتلة
يبدو من المعقول أيضًا أن يكون التسارع يتناسب عكسيا مع كتلة النظام. وبعبارة أخرى، كلما زادت الكتلة (القصور الذاتي)، كلما كان التسارع أصغر عند قوة معينة. كما هو موضح في الشكل 5.11، فإن نفس القوة الخارجية الصافية المطبقة على كرة السلة تنتج تسارعًا أصغر بكثير عندما يتم تطبيقه على سيارات الدفع الرباعي. تتم كتابة التناسب العكسي كما يلي:
a ∝ 1/m
حيث m هي كتلة النظام و a هي مقدار التسارع. أظهرت التجارب أن التسارع يتناسب عكسيًا مع الكتلة، تمامًا كما يتناسب طرديًا مع القوة الخارجية الصافية أو محصلة القوى.
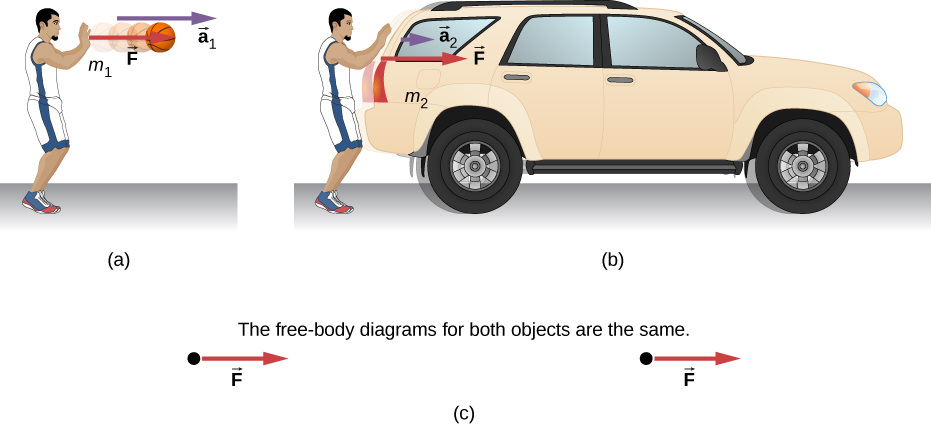
الشكل 5.11: نفس القوة التي تؤثر على أنظمة كتل مختلفة تنتج تسارعًا مختلفًا:
- (a) يدفع لاعب كرة السلة كرة سلة لتمرير الكرة. (تجاهل تأثير الجاذبية على الكرة).
- (b) يؤثر نفس اللاعب بنفس القوة على سيارة الدفع الرباعي المتوقفة وينتج تسارعًا أقل بكثير.
- (c) مخططات الجسم الحر متطابقة، مما يسمح بالمقارنة المباشرة للحالتين.
ستظهر سلسلة من أنماط الرسوم البيانية للجسم الحر وأنت تواجه المزيد من المسائل وتتعلم كيفية رسمها عند رسم مخططات الجسم الحر.
لقد وُجد أن تسارع جسم ما يعتمد فقط على القوة الخارجية الصافية (محصلة القوى) وكتلة الجسم. ومن خلال الجمع بين التناسبين، نحصل مباشرة على قانون نيوتن الثاني كما يلي:
استنتاج نص قانون نيوتن الثاني
يتناسب تسارع النظام طرديًا مع القوة الخارجية الصافية (محصلة القوى) التي تؤثر عليه وعكسيًا مع كتلة الجسم.
وبترجمة هذا التعريف إلى شكل معادلة رياضية، فيكون قانون نيوتن الثاني هو:
a⃗ = F⃗ net . m
حيث:
a⃗ هي التسارع، F⃗ ne هي القوة الصافية (محصلة القوى)، وm هي الكتلة.
غالبًا ما يتم كتابة هذه المعادلة على الشكل الأكثر انتشارًا كما يلي:
F⃗ net = ∑ F = m . a
(5.3)
لكن المعادلة الأولى تعطي نظرة ثاقبة على معنى قانون نيوتن الثاني. عند النظر في مقدار القوة والتسارع فقط، يمكن كتابة معادلة قانون نيوتن الثاني في شكل قياسي أبسط كما يلي:
F⃗ net = m . a
(5.4)
القانون هو علاقة السبب والنتيجة بين ثلاث كميات لا تعتمد ببساطة على تعريفاتها. تعتمد صحة القانون الثاني على التحقق التجريبي. يعد الرسم البياني للجسم الحر، الذي ستتعلمه لرسم مخططات الجسم الحر، أساسًا لكتابة قانون نيوتن الثاني.
أمثلة وتطبيقات على قانون نيوتن الثاني
مثال 5.2 : ما هو التسارع الذي يمكن أن ينتجه الشخص عند دفع جزازة العشب؟
افترض أن صافي القوة الخارجية (قوة الدفع ناقص الاحتكاك) التي تؤثر على جزازة العشب هي 51 نيوتن (حوالي 11 رطلاً) في اتجاه موازِ للأرض (الشكل 5.12). وكتلة الجزازة 24 كجم. ما هو تسارعها؟
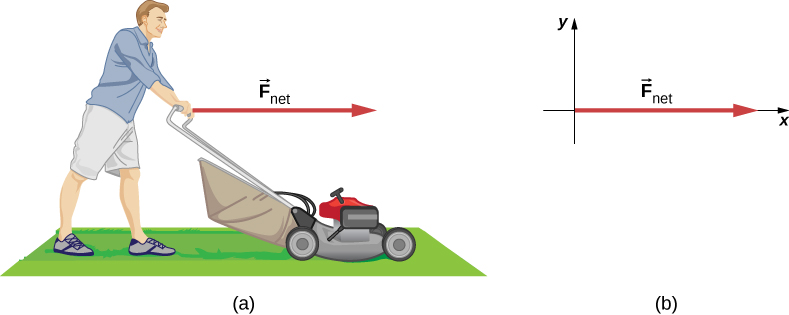
الشكل 5.12: (أ) القوة الكلية المؤثرة على جزازة العشب هي 51 نيوتن جهة اليمين. بأي معدل يكون تسارع جزازة العشب إلى اليمين؟ (ب) يظهر مخطط الجسم الحر لهذه المسألة.
إستراتيجية الحل
تتضمن هذه المسألة الحركة في الاتجاه الأفقي فقط؛ نحصل أيضًا على القوة الكلية، المشار إليها بواسطة متجه واحد، ولكن يمكننا إهمال طبيعة المتجه والتركيز على تطبيق قانون نيوتن الثاني. نظرًا لأن المعطيات في المسألة هي القوة الكلية Fnet والكتلة m، يمكن حساب التسارع مباشرة من قانون نيوتن الثاني حيث: Fnet = m * a.
الحل
مقدار التسارع a:
a = Fnet / m
بالتعويض عن القيم المعروفة ينتج لنا:
a = 51 N / 24 kg
الآن نستبدل وحدة النيوتن N بما يكافئها، وهو الكيلوجرام في المتر على الثانية المربعة، لأن:
1 نيوتن = 1 كيلوجرام * متر / ثانية 2
ينتج لنا:
a = 51 (kg . m / s2) / 24 kg
a = 2.1 m / s2
الدلالة
اتجاه التسارع هو نفس اتجاه القوة الكلية الموازية للأرض.
هذا نتيجة للعلاقة المتجهة المعبر عنها في قانون نيوتن الثاني، وهي أن المتجه الذي يمثل صافي القوة هو حاصل الضرب القياسي لمتجه التسارع في الكتلة. لا توجد معلومات معطاة في هذا المثال حول القوى الخارجية الفردية التي تعمل على النظام، ولكن يمكننا أن نقول شيئًا عن مقاديرها النسبية. على سبيل المثال، يجب أن تكون القوة التي يبذلها الشخص الذي يدفع الجزازة أكبر من الاحتكاك المعاكس للحركة (بما أننا نعلم أن الجزازة تتحرك للأمام)، ويجب أن تلغي القوى الرأسية لأنه لا يوجد تسارع في الاتجاه العمودي (الجزازة تتحرك فقط أفقيًا). التسارع الموجود صغير بما يكفي ليكون معقولاً لشخص يدفع جزازة. لن يستمر مثل هذا الجهد لفترة طويلة، لأنه سيتم الوصول إلى السرعة القصوى للشخص قريبًا.
القوة الكلية وتعدد القوى
في المثال السابق، تعاملنا مع صافي القوة أو القوة الكلية من أجل التبسيط فقط. ومع ذلك، تعمل عدة قوى على جزازة العشب. الوزن w⃗ (الذي تمت مناقشته بالتفصيل في موضوع الكتلة والوزن) يؤثر على الجزازة باتجاه مركز الأرض؛ ينتج عن هذا قوة دفع على الأرض. يجب أن تمارس الأرض قوة تصاعدية على جزازة العشب، والمعروفة باسم القوة الطبيعية N⃗، والتي نحددها في موضوع القوى الشائعة. هذه القوى متوازنة وبالتالي لا تنتج تسارعًا رأسيًا. في المثال التالي، نعرض كلا هاتين القوتين. بينما تستمر في حل المسائل باستخدام قانون نيوتن الثاني، تأكد من إظهار قوى متعددة.
تحقق من فهمك
في وقت إطلاقها، كانت سفينة تايتانيك Titanic أضخم كائن متحرك تم بناؤه على الإطلاق، حيث بلغت كتلتها 6.0 × 107 كجم. إذا تم تطبيق قوة مقدارها 6 مليون نيوتن (6 × 106 N) على السفينة، فما التسارع الذي ستشهده؟
مثال 5.3: المقارنة بين القوى – أي قوة أكبر؟
- (أ) تتحرك السيارة الموضحة في الشكل 5.13 بسرعة ثابتة. ما هي القوة الأكبر، قوة الاحتكاك F⃗ friction أم قوة السحب F⃗ drag اشرح إجابتك.
- (ب) نفس السيارة تتسارع الآن جهة اليمين. ما هي القوة الأكبر، قوة الاحتكاك F⃗ friction أم قوة السحب F⃗ drag اشرح إجابتك.
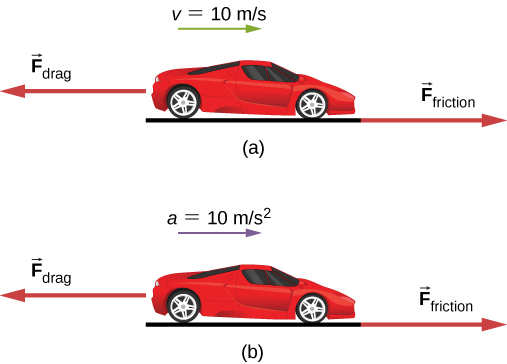
الشكل 5.13 تظهر سيارة (أ) تتحرك بسرعة ثابتة و (ب) تتسارع. كيف تقارن القوى المؤثرة على السيارة في كل حالة؟
- (أ) ما الذي تخبرنا به معرفة أن السيارة تتحرك بسرعة ثابتة عن صافي القوة الأفقية المؤثرة على السيارة مقارنةً بقوة الاحتكاك؟
- (ب) ما الذي تخبرنا به معرفة تسارع السيارة عن القوة الأفقية المؤثرة على السيارة مقارنة بقوة الاحتكاك؟
إستراتيجية الحل
يجب أن ننظر في قوانين نيوتن الأول وقانون نيوتن الثاني لتحليل الوضع. نحن بحاجة إلى تحديد القانون الذي ينطبق؛ وهذا بدوره سيخبرنا عن العلاقة بين القوى.
الحل
أ. القوى متساوية. وفقًا لقانون نيوتن الأول، إذا كانت القوة الكلية هي صفر، فإن السرعة تكون ثابتة.
ب. في هذه الحالة، يجب أن تكون قوة الاحتكاك F⃗ friction أكبر من قوة السحب F⃗ drag. وفقًا لقانون نيوتن الثاني، فإن صافي القوة مطلوب لإحداث التسارع.
الدلالة
قد تبدو هذه الأسئلة تافهة، ولكن عادة ما يتم الرد عليها بشكل غير صحيح. لكي تتحرك سيارة أو أي جسم آخر، يجب تسريعها من السكون إلى السرعة المطلوبة؛ هذا يتطلب أن تكون قوة السحب أكبر من قوة الاحتكاك. وبمجرد أن تتحرك السيارة بسرعة ثابتة، يجب أن تكون القوة الكلية مساوية صفرًا؛ خلاف ذلك، سوف تتسارع السيارة (تكتسب السرعة).
من أجل حل المسائل المتعلقة بقوانين نيوتن، يجب أن نفهم ما إذا كان يجب تطبيق قانون نيوتن الأول (حيث ΣF⃗ =0⃗) أو قانون نيوتن الثاني (حيث ΣF⃗ لا تساوي صفرًا). سيكون هذا واضحًا عندما ترى المزيد من الأمثلة وتحاول حل المسائل بنفسك.
مثال 5.4: الدفع الصاروخي الذي يسرع الزلاجة الصاروخية
قبل الرحلات الفضائية المأهولة، يتم استخدام الزلاجات الصاروخية لاختبار الطائرات ومعدات الصواريخ والتأثيرات الفسيولوجية على البشر بسرعات عالية. كانت تتألف من منصة مثبتة على قضيب أو اثنين وتُدفع بعدة صواريخ.
احسب مقدار القوة التي يؤثر بها كل صاروخ، وتسمى قوة الدفع T، لنظام الدفع رباعي الصواريخ الموضح في الشكل 5.14. التسارع الأولي للزلاجة هو 49 متر / ثانية 2، وكتلة النظام 2100 كجم، وقوة الاحتكاك التي تعارض الحركة هي 650 نيوتن.
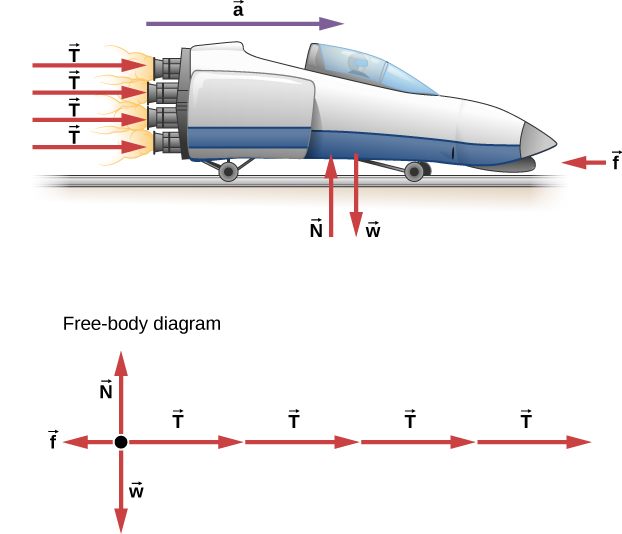
يخلق كل صاروخ قوة دفع متطابقة T. النظام هنا هو الزلاجة وصواريخها وراكبها، لذلك لا يتم أخذ أي من القوى الموجودة بين هذه الأجسام في الاعتبار. (السهم الذي يمثل الاحتكاك (f⃗) وهو مرسوم أكبر من مقياس الرسم)
إستراتيجية الحل
على الرغم من أن القوى تعمل رأسيًا وأفقيًا، فإننا نفترض أن القوى الرأسية تلغي لأنه لا يوجد تسارع رأسي. هذا يتركنا مع القوى الأفقية فقط ومسألة أحادية البعد أبسط.
يشار إلى الاتجاهات بعلامات زائد أو ناقص، مع أخذ اليمين باعتباره الاتجاه الموجب. انظر مخطط الجسم الحر في الشكل 5.14.
الحل
بما أنه يتم إعطاء التسارع والكتلة وقوة الاحتكاك، نبدأ بقانون نيوتن الثاني ونبحث عن طرق لإيجاد قوة الدفع للمحركات. لقد حددنا اتجاه القوة والتسارع على أنهما يعملان “جهة اليمين”، لذلك نحتاج إلى مراعاة مقادير هذه الكميات فقط في الحسابات. ومن ثم نبدأ بمعادلة قانون نيوتن الثاني كما يلي:
F⃗ net = m . a
حيث Fnet هي القوة الكلية (محصلة القوى) على طول الاتجاه الأفقي. يمكننا أن نرى من الشكل أن قوة دفع المحركات يتم جمعها، بينما قوة الاحتكاك تقاوم الدفع. في شكل معادلة، القوة الخارجية الصافية تكون مساوية لما يلي:
F⃗ net = 4 T – f
بالتعويض عن ذلك في قانون نيوتن الثاني يعطينا:
F⃗ net = m . a = 4 T – f
باستخدام القليل من الجبر، يمكن حل هذه المعادلة بالنسبة ل 4T كما يلي:
4 T = m . a + f
بالتعويض عن القيم المعروفة ينتج لنا:
4 T = m . a + f = (2100 kg)(49 m/s2) + 650 N
إذن، فإن الناتج الإجمالي لقوة الدفع الصاروخي هي:
4 T = 1.0 x 105 N
وقوة كل صاروخ هي (بالقسمة على 4):
T = 2.5 x 104 N
الدلالة
الأرقام كبيرة جدًا، لذا قد تفاجئك النتيجة. تم إجراء تجارب مثل هذه في أوائل الستينيات من القرن الماضي لاختبار حدود التحمل البشري، وقد تم تصميم الإعداد لحماية الأشخاص البشريين في عمليات القذف الطارئة للمقاتلات النفاثة. تم الحصول على سرعات 1000 كم / ساعة، مع تسارع مقداره 45 ضعف تسارع الجاذبية الأرضية. (تذكر أن التسارع بسبب الجاذبية هو 9.80 متر/ثانية2). عندما نقول أن التسارع 45 ضعف تسارع الجاذبية، فهذا يعني أنه 45 × 9.8 متر / ثانية2، أي ما يقرب من 440 متر / ثانية2). وعلى الرغم من عدم استخدام الكائنات الحية بعد الآن، تم الحصول على سرعات أرضية تبلغ مقدارها 10000 كم / ساعة باستخدام مزلقة صاروخية.
في هذا المثال، كما في المثال السابق، يكون النظام محل البحث واضحًا. نرى في الأمثلة اللاحقة أن اختيار النظام أمر بالغ الأهمية، وأن الخيار ليس دائمًا واضحًا.
قانون نيوتن الثاني هو أكثر من مجرد تعريف. إنها علاقة بين التسارع والقوة والكتلة. يمكن أن يساعدنا في عمل تنبؤات. يمكن تعريف كل من هذه الكميات الفيزيائية بشكل مستقل، لذلك يخبرنا قانون نيوتن الثاني بشيء أساسي وعالمي عن الطبيعة.
تحقق من فهمك
تصطدم سيارة رياضية تزن 550 كجم بشاحنة تزن 2200 كجم، وأثناء التصادم، تكون القوة الكلية على كل مركبة هي القوة التي تمارسها المركبة الأخرى. إذا كان مقدار تسارع الشاحنة 10 متر / ثانية2، فما مقدار تسارع السيارة الرياضية؟
قانون نيوتن الثاني بصورة المكوّنات المتجهة
لقد طورنا قانون نيوتن الثاني وقدمناه كمعادلة متجهة في المعادلة رقم 5.3. يمكن كتابة هذه المعادلة المتجهة على صورة معادلات المكوّنات المتجهة والتي تتألف من ثلاثة اتجاهات كما يلي:
قانون نيوتن الثاني هو وصف لكيفية استجابة الجسم ميكانيكيًا لبيئته. تأثير البيئة هو صافي القوة المؤثرة على الجسمFnet → ، واستجابة الجسم هي التسارع a →، وقوة الاستجابة تتناسب عكسيًا مع الكتلة m. كلما زادت كتلة الجسم، قلت استجابته (تسارعه) بالنسبة لتأثير بيئة معيّن (قوة صافية معينة تؤثر عليه). لذلك، فإن كتلة الجسم هي مقياس لقصورها الذاتي، كما أوضحنا في قانون نيوتن الأول.
مثال 5.5: القوة المؤثرة على كرة القدم
تم ركل كرة قدم بوزن 0.400 كجم عبر الملعب بواسطة أحد اللاعبين؛ تخضع الكرة لتسارع يتم حسابه باستخدام المعادلة التالية:
أوجد (أ) القوة المحصلة (محصلة القوى) المؤثرة على الكرة، (ب) مقدار واتجاه القوة المحصلة.
إستراتيجية الحل
المتجهات في تنسيق i ^ و j ^، والتي تشير إلى اتجاه القوة على طول المحور x والمحور y، على التوالي، متضمنة في المعطيات، لذلك نطبق قانون نيوتن الثاني في صورة المكوّنات المتجهة.
الحل
(أ) نطبق قانون نيوتن الثاني بالتعويض عن القيم المُعطاة:
(ب) يتم إيجاد مقدار واتجاه القوة المحصلة باستخدام مكوّنات متجه القوة المحصلة F⃗ net:
الدلالة
يجب أن نتذكر أن قانون نيوتن الثاني هو معادلة متجهة. في (أ)، نقوم بضرب كمية متجهة في كمية قياسية (عدد) لتحديد القوة الكلية في شكل متجه. بينما يعطي شكل المتجه للقوة الكلية تمثيلًا مضغوطًا لمتجه القوة الكلية، إلا أنه لا يخبرنا بمدى “مقداره”، أو إلى أين يتجه بالفعل باستخدام المصطلحات البديهية. أما في الجزء (ب)، قمنا بتحديد المقدار الفعلي (القيمة المطلقة) لهذه القوة، والاتجاه الفعلي الذي تنتقل فيه.
مثال 5.6: حساب الكتلة باستخدام قانون نيوتن الثاني
أوجد كتلة السيارة إذا كانت القوة الكلية المؤثرة – 600.0jˆN تنتج تسارع −0.2j^m/s2.
إستراتيجية الحل
لم يتم تعريف تقسيم المتجه، لذلك لا يمكن تطبيق المعادلة m=F⃗ net/a⃗. ومع ذلك، فإن الكتلة m هي كمية عددية غير متجهة، لذلك يمكننا استخدام الشكل القياسي لقانون نيوتن الثاني: m = Fnet / a.
الحل
نستخدم المعادلة: m = Fnet / a ونقوم بالتعويض عن القيم المطلقة للمتجهين، القوة Fnet = 600 N والتسارع a = 0.2 m/s2، وبالتالي نحصل على:
الدلالة
أُعطيت القوة والتسارع بالصيغة i ^ و j ^، لكن الإجابة، الكتلة m، هي كمية عددية، وبالتالي فهي غير معطاة بالصيغة i ^ و j ^.
مثال 5.7: تأثير عدة قوى على الجسيم
جسيم كتلته m = 4.0 kg يتأثر بأربع قوى مقدارها على التوالي: F1 = 10.0 N وF2 = 40.0 N و F3 = 5.0 N و F4 = 2.0 N، مع الاتجاهات كما هو موضح في مخطط الجسم الحر في الشكل 5.15. ما هو تسارع الجسيم؟
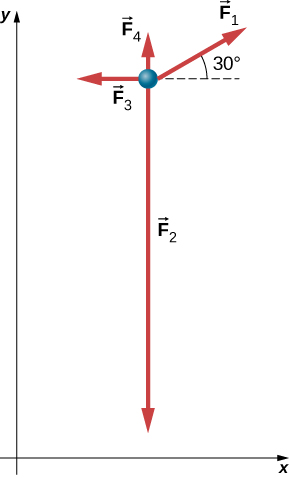
إستراتيجية الحل
نظرًا لأن هذه مسألة ثنائية الأبعاد، يجب أن نستخدم مخطط الجسم الحر. أولاً، يجب تحليل متجه القوة F1 → إلى مكوناته بالاتجاهين x و y. يمكننا بعد ذلك تطبيق القانون الثاني في كل اتجاه للمحورين.
الحل
نرسم مخططًا للجسم الحر كما هو موضح في الشكل 5.15. الآن نطبق قانون نيوتن الثاني. نحن نأخذ بالاعتبار جميع المتجهات التي تم تفكيكها إلى مكونات x و y:
تجميع النتائج
بالتالي، فإن محصلة أو صافي التسارع هو:
وهو متجه مقداره (قيمته المطلقة) تساوي 8.4 m/s2 موجه بزاوية 276 درجة إلى المحور السيني الموجب.
الدلالة
يمكن إيجاد العديد من الأمثلة في الحياة اليومية التي تتضمن ثلاث قوى أو أكثر تؤثر على جسم واحد، مثل الكابلات الممتدة من جسر البوابة الذهبية أو لاعب كرة قدم أمريكية يتم التعامل معه من قبل ثلاثة مدافعين، يمكننا أن نرى أن حل هذه الأمثلة هو فقط امتدادًا لما قمنا به بالفعل.
تأكد من فهمك
سيارة لها قوى تؤثر عليها، كما هو موضح في الشكل أدناه. كتلة السيارة 1000.0 كجم. الطريق أملس، لذا يمكن تجاهل قوة الاحتكاك. (أ) ما هي القوة الكلية المؤثرة على السيارة؟ (ب) ما هي عجلة (تسارع) السيارة؟
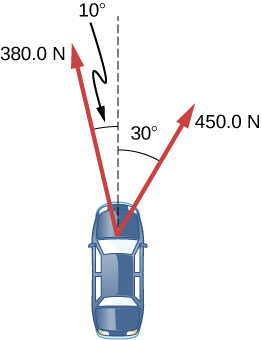
قانون نيوتن الثاني وزخم الحركة
أعلن نيوتن في الواقع عن قانونه الثاني بدلالة زخم الحركة Momentum وهو كما يلي:
“المعدل اللحظي الذي يتغير فيه زخم الجسم يساوي صافي القوة المؤثرة على الجسم”. (يشير “المعدل اللحظي” إلى أن دالة المشتقة متضمنة).
يمكن التعبير عن هذا من خلال معادلة المتجه التالية:
(5.6)
هذا يعني أن قانون نيوتن الثاني يعالج السؤال المركزي للحركة: ما الذي يسبب التغيير في حركة الجسم؟ وصف نيوتن الزخم بأنه “كمية الحركة” quantity of motion، وهي طريقة للجمع بين سرعة الجسم وكتلته. تم تخصيص موضوع الزخم الخطي والتصادم لدراسة الزخم بالتفصيل.
في الوقت الحالي، يكفي تعريف الزخم p⃗ باعتباره حاصل ضرب كتلة الجسم m في سرعته v⃗:
(5.7)
وذلك لأن السرعة كمية متجهة، وكذلك الزخم.
أمثلة على الزخم
من السهل تصور الزخم. القطار الذي يتحرك بسرعة 10 م / ث لديه زخم أكثر من القطار الذي يتحرك بسرعة 2 م / ث. في الحياة اليومية، نتحدث عن فريق رياضي واحد على أنه “يتمتع بزخم” عندما يسجل نقاطًا ضد الفريق المنافس.
إذا قمنا بالتعويض عن المعادلة 5.7 في المعادلة 5.6، نحصل على ما يلي:
وعندما تكون m ثابتة، يكون لدينا:
وهكذا، نرى أن شكل الزخم لقانون نيوتن الثاني يتقلص إلى الشكل المعطى سابقًا في هذا القسم.
المراجع
- موسوعة الفيزياء العامة، ترجمة وإعداد: د. م. مصطفى عبيد، مركز البحوث والدراسات متعدد التخصصات، إسطنبول، 2022-2023.
- كتاب الفيزياء للجامعات، صموئيل جيه لينغ، جامعة ولاية ترومان، د. جيف ساني، جامعة لويولا ماريماونت ويليام مويبس.





