جبر المتجهات وحل معادلات المتجهات

بنهاية هذا القسم من جبر المتجهات، سيكون القارئ قادرًا على:

تطبيق الطرق التحليلية في جبر المتجهات لإيجاد محصلة المتجهات ولحل المعادلات المتجهة للمتجهات المجهولة.
تفسير المواقف الفيزيائية بدلالة التعبيرات المتجهة.

المحتويات

يمكن جمع المتجهات معًا وضربها في أعداد (الضرب القياسي). جمع المتجهات هي عملية تجميعية (المعادلة 2.8) وتبادلية (المعادلة 2.7)، وضرب المتجه بمجموع أعداد قياسية هي عملية توزيعية (المعادلة 2.9). أيضًا، ضرب عدد قياسي بمجموع متجهات هي عملية توزيعية:

α (\vec{A} + \vec{B}) = α \vec{A} + α \vec{B} .

(2.22)

في هذه المعادلة، α هي أي عدد (قياسي). على سبيل المثال، يمكن التعبير عن المتجه الموازي للمتجه:

\vec{A} = A_{x} \hat{i} + A_{y} \hat{j} + A_{z} \hat{k}

ببساطة بضرب المتجه A⃗ في العدد القياسي α = −1:

− \vec{A} = − A_{x} \hat{i} - A_{y} \hat{j} - A_{z} \hat{k} .

(2.23)

مثال1: محصلة اتجاه الحركة

في نظام الإحداثيات الديكارتية حيث تشير i^ إلى الشرق الجغرافي، و j^ تشير إلى الشمال الجغرافي، و k^ تشير إلى الارتفاع فوق مستوى سطح البحر، تتقدم قافلة عسكرية بموقعها عبر منطقة غير معروفة بسرعة:

\vec{v} = (4.0 \hat{i} + 3.0 \hat{j} + 0.1 \hat{k}) km / h

إذا كان على القافلة أن تنسحب، في أي اتجاه جغرافي ستتحرك؟

الحل

يحتوي متجه السرعة على المكون الثالث ^v⃗ _z=(+0.1km/h)kˆ، والذي يقول إن القافلة تصعد بمعدل 100 متر / ساعة عبر التضاريس الجبلية. في الوقت نفسه، تبلغ سرعتها 4.0 كم / س إلى الشرق و3.0 كم / س إلى الشمال، لذلك فهي تتحرك على الأرض في اتجاه: tan⁻¹(3/4) ≈ 37 درجة شمال الشرق. إذا كان على القافلة أن تتراجع، فإن متجه سرعتها الجديد u⃗ يجب أن يكون عكسيًا لـ v⃗ وأن يكون على الشكل u⃗ =−αv⃗، حيث α هو رقم موجب. وبالتالي، فإن سرعة التراجع ستكون:

\vec{u} = α (−4.0 \hat{i} - 3.0 \hat{j} - 0.1 \hat{k}) km / h

تشير العلامة السالبة للمكون الثالث إلى أن القافلة ستنزل. زاوية اتجاه سرعة التراجع هي tan ⁻¹ (−3α /- 4α) ≈ 37 درجة جنوب الغرب. لذلك، ستتحرك القافلة على الأرض في اتجاه 37 درجة جنوب الغرب أثناء نزولها في طريق العودة.

يُطلق على تعميم الرقم صفر على الجبر المتجه اسم المتجه الصفري، ويُشار إليه بالرمز →0. جميع مكونات المتجه الصفري هي صفر:

\vec{0} = 0 \hat{i} + 0 \hat{j} + 0 \hat{k}

وبالتالي فإن المتجه الفارغ ليس له طول ولا اتجاه.

قاعدة التساوي في جبر المتجهات

في حبر المتجهات، المتجهان A⃗ و B⃗ هما متجهان متساويان إذا وفقط إذا كان الفرق بينهما هو المتجه الصفري:

\vec{0} = \vec{A} - \vec{B} = (A_{x} \hat{i} + A_{y} \hat{j} + A_{z} \hat{k}) - (B_{x} \hat{i} + B_{y} \hat{j} + B_{z} \hat{k}) = (A_{x} - B_{x}) \hat{i} + (A_{y} - B_{y}) \hat{j} + (A_{z} - B_{z}) \hat{k} .

تعني معادلة المتجه هذه أنه يجب أن يكون لدينا A_x – B_x = 0 و A_y – B_y = 0 و A_z – B_z = 0. ومن ثم، يمكننا كتابة أن المتجهات A⃗ = B⃗ إذا وفقط إذا كانت المكونات المقابلة للمتجهات A⃗ و B⃗ متساوية:

\vec{A} = \vec{B} \Leftrightarrow {\begin{matrix} A_{x} = B_{x} \\ A_{y} = B_{y} \\ A_{z} = B_{z} \end{matrix} .

(2.24)

ونستنج من ذلك أن المتجهين متساويان عندما تتساوى مكوناتهما العددية المقابلة.

يتيح لنا تحليل المتجهات إلى مكوناتها العددية (أي التعبير عنها بدلالة مكوناتها العددية) والتعبير عنها تحليليًا في شكل مكون متجهي (المعطى في المعادلة 2.19) استخدام جبر المتجهات لإيجاد المجاميع أو الفروقات بين العديد من المتجهات بشكل تحليلي (أي بدون استخدام أساليب الرسوم البياني). على سبيل المثال، لإيجاد محصلة متجهين A وB، نجمعهم ببساطة مكونًا تلو الآخر، على النحو التالي:

\vec{R} = \vec{A} + \vec{B} = (A_{x} \hat{i} + A_{y} \hat{j} + A_{z} \hat{k}) + (B_{x} \hat{i} + B_{y} \hat{j} + B_{z} \hat{k}) = (A_{x} + B_{x}) \hat{i} + (A_{y} + B_{y}) \hat{j} + (A_{z} + B_{z}) \hat{k} .

بهذه الطريقة، باستخدام المعادلة 2.24، فإن المركبات أو المكونات العددية للمتجه الناتج:

\vec{R} = R_{x} \hat{i} + R_{y} \hat{j} + R_{z} \hat{k}

هي مجموع المكونات العددية المقابلة للمتجهات A وB:

{\begin{matrix} R_{x} = A_{x} + B_{x}, \\ R_{y} = A_{y} + B_{y}, \\ R_{z} = A_{z} + B_{z} . \end{matrix}

محصلة عدد من المتجهات

في جبر المتجهات يمكن استخدام الطرق التحليلية لإيجاد مكونات محصلة العديد من المتجهات. على سبيل المثال، إذا أردنا جمع المتجهات F⃗ ₁,F⃗ ₂,F⃗ ₃,…,F⃗ _N حيث يكون كل متجه F⃗ _k=F_kxiˆ+F_kyjˆ+F_kzkˆ. تكون المحصلة هي المتجه F_R حيث:

\begin{matrix} {\vec{F}}_{R} = {\vec{F}}_{1} + {\vec{F}}_{2} + {\vec{F}}_{3} + … + {\vec{F}}_{N} & = \sum_{k = 1}^{N} {\vec{F}}_{k} = \sum_{k = 1}^{N} (F_{k x} \hat{i} + F_{k y} \hat{j} + F_{k z} \hat{k}) \\ = (\sum_{k = 1}^{N} F_{k x}) \hat{i} + (\sum_{k = 1}^{N} F_{k y}) \hat{j} + (\sum_{k = 1}^{N} F_{k z}) \hat{k} . \end{matrix}

لذلك، فإن المكونات العددية المتجه المحصلة هي:

{\begin{matrix} F_{R x} = \sum_{k = 1}^{N} F_{k x} = F_{1 x} + F_{2 x} + … + F_{N x} \\ F_{R y} = \sum_{k = 1}^{N} F_{k y} = F_{1 y} + F_{2 y} + … + F_{N y} \\ F_{R z} = \sum_{k = 1}^{N} F_{k z} = F_{1 z} + F_{2 z} + … + F_{N z} . \end{matrix}

(2.25)

بعد إيجاد المكونات العددية، يمكننا كتابة المحصلة في شكل مكونات المتجه:

{\vec{F}}_{R} = F_{R x} \hat{i} + F_{R y} \hat{j} + F_{R z} \hat{k} .

تعتبر الطرق التحليلية لإيجاد المحصلة، وبشكل عام لحل المعادلات في جبر المتجهات، مهمة جدًا في الفيزياء لأن العديد من الكميات الفيزيائية هي كميات متجهة. على سبيل المثال، نستخدم هذه الطريقة في علم الحركة لإيجاد متجهات محصلة الإزاحة ومتجهات محصلة السرعة، وفي الميكانيكا لإيجاد متجهات محصلة القوى التي تؤثر على جسم، ونتائج العديد من الكميات المتجهة المشتقة الأخرى، وفي الكهرباء والمغناطيسية لإيجاد محصلة الحقول الكهربائية أو المغناطيسية.

مثال2: الحساب التحليلي للمحصلة

يتم تحديد ثلاث متجهات إزاحة A⃗ , B⃗ , C⃗ في مستوى (الشكل 2.13) بمقاديرها A = 10.0، B = 7.0، وC = 8.0، على التوالي، وزوايا الاتجاه الخاصة بكل منها مع الاتجاه الأفقي α = 35 درجة، β = -110 درجة، وγ = 30 درجة. الوحدات الفيزيائية للمقادير هي السنتيمتر. حلل المتجهات إلى مكوناتها العددية وأوجد مجاميع المتجهات التالية:

(a) R⃗ =A⃗ +B⃗ +C⃗

(b) D⃗ =A⃗ −B⃗

and (c) S⃗ =A⃗ −3B⃗ +C⃗

إستراتيجية الحل

أولاً، نستخدم المعادلة 2.17 لإيجاد المكونات العددية لكل متجه ثم نعبر عن كل متجه في شكل مكون المتجه المعطى بواسطة المعادلة 2.12. بعد ذلك، نستخدم الطرق التحليلية في جبر المتجهات لإيجاد النتائج المطلوبة.

الحل

نحلل المتجهات المعطاة إلى مكوناتها العددية:

\begin{array}{l} {\begin{array}{l} A_{x} = A cos α = (10.0 cm) cos 35 ° = 8.19 cm \\ A_{y} = A sin α = (10.0 cm) sin 35 ° = 5.73 cm \end{array} \\ {\begin{array}{l} B_{x} = B cos β = (7.0 cm) cos (−110 °) = −2.39 cm \\ B_{y} = B sin β = (7.0 cm) sin (−110 °) = −6.58 cm \end{array} \\ {\begin{array}{l} C_{x} = C cos γ = (8.0 cm) cos 30 ° = 6.93 cm \\ C_{y} = C sin γ = (8.0 cm) sin 30 ° = 4.00 cm \end{array} \end{array} .

بالنسبة إلى المطلوب في (أ) قد نعوض مباشرة في المعادلة رقم 2.25 لإيجاد المكونات العددية للنتيجة المطلوبة:

{\begin{array}{l} R_{x} = A_{x} + B_{x} + C_{x} = 8.19 cm - 2.39 cm + 6.93 cm = 12.73 cm \\ R_{y} = A_{y} + B_{y} + C_{y} = 5.73 cm - 6.58 cm + 4.00 cm = 3.15 cm \end{array} .

لذلك، فإن المحصلة تكون هي المتجه R:

\vec{R} = R_{x} \hat{i} + R_{y} \hat{j} = (12.7 \hat{i} + 3.1 \hat{j}) cm

المطلوب في ب

بالنسبة إلى (ب)، قد نرغب في كتابة الفرق بين المتجهات كما يلي:

\vec{D} = \vec{A} - \vec{B} = (A_{x} \hat{i} + A_{y} \hat{j}) - (B_{x} \hat{i} + B_{y} \hat{j}) = (A_{x} - B_{x}) \hat{i} + (A_{y} - B_{y}) \hat{j} .

ثم، المكونات العددية للفرق بين المتجهات هي:

{\begin{array}{l} D_{x} = A_{x} - B_{x} = 8.19 cm - (−2.39 cm) = 10.58 cm \\ D_{y} = A_{y} - B_{y} = 5.73 cm - (−6.58 cm) = 12.31 cm \end{array} .

وبالتالي يكون المتجه الناتج عن عملية الطرح هو:

\vec{D} = D_{x} \hat{i} + D_{y} \hat{j} = (10.6 \hat{i} + 12.3 \hat{j}) cm

المطلوب في ج

بالنسبة إلى (ج)، يمكننا كتابة المتجه S بالشكل الصريح التالي:

\begin{matrix} \vec{S} & = \vec{A} - 3 \vec{B} + \vec{C} = (A_{x} \hat{i} + A_{y} \hat{j}) - 3 (B_{x} \hat{i} + B_{y} \hat{j}) + (C_{x} \hat{i} + C_{y} \hat{j}) \\ = (A_{x} - 3 B_{x} + C_{x}) \hat{i} + (A_{y} - 3 B_{y} + C_{y}) \hat{j} . \end{matrix}

ثم، المكونات العددية لمتجه S هي:

{\begin{array}{l} S_{x} = A_{x} - 3 B_{x} + C_{x} = 8.19 cm - 3 (−2.39 cm) + 6.93 cm = 22.29 cm \\ S_{y} = A_{y} - 3 B_{y} + C_{y} = 5.73 cm - 3 (−6.58 cm) + 4.00 cm = 29.47 cm \end{array} .

ويكون المتجه S هو:

\vec{S} = S_{x} \hat{i} + S_{y} \hat{j} = (22.3 \hat{i} + 29.5 \hat{j}) cm

الدلالة

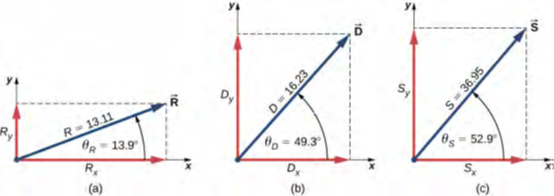
في جبر المتجهات وبعد إيجاد مكونات المتجه، يمكننا توضيح المتجهات بالرسم البياني أو يمكننا حساب المقادير وزوايا الاتجاه، كما هو موضح في الشكل 2.24. يمكن مقارنة نتائج المقادير في (ب) و (ج) مع نتائج نفس المسائل التي تم الحصول عليها باستخدام الطريقة الرسومية، كما هو موضح في الشكل 2.14 والشكل 2.15.

لاحظ أن الطريقة التحليلية تعطي نتائج دقيقة وأن دقتها لا تقتصر على دقة المسطرة أو المنقلة فقط، كما كان الحال مع الطريقة الرسومية المستخدمة في المثال 2.2 للعثور على نفس النتيجة.

جبر المتجهات - الشكل 2.24 توضيح رسومي للحلول التي تم الحصول عليها تحليليًا في المثال السابق. — جبر المتجهات – الشكل 2.24 توضيح رسومي للحلول التي تم الحصول عليها تحليليًا في المثال السابق.

تحقق من فهمك

تم تحديد ثلاث متجهات إزاحة A⃗ , B⃗ , F⃗ (الشكل 2.13) بمقاديرها A = 10.00 و B = 7.00 و F = 20.00 على التوالي وبزوايا اتجاه كل منها مع الاتجاه الأفقي α = 35 درجة، β = -110 درجة، وφ = 110 درجة. الوحدات الفيزيائية للمقادير هي السنتيمتر. استخدم الطريقة التحليلية لإيجاد المتجه G⃗ =A⃗ +2B⃗ −F⃗. تحقق من أن G = 28.15 سم وأن θ_G = −68.65 درجة.

مثال3: لعبة شد الحبل

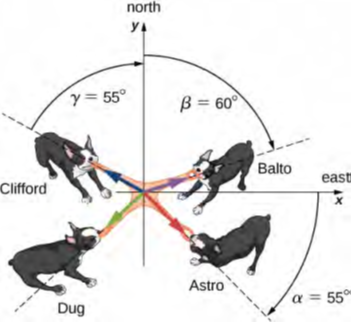
أربعة كلاب تُدعى Astro وBalto وClifford وDug تلعب لعبة شد الحبل مع لعبة (الشكل 2.25). يسحب Astro اللعبة في الاتجاه α = 55 درجة جنوب الشرق، يسحب Balto في الاتجاه β = 60 درجة شرقًا من الشمال، ويسحب Clifford في الاتجاه γ = 55 درجة غربًا من الشمال. يسحب Astro بقوة مقدارها 160.0 وحدة قوة (N)، والتي نختصرها كـ A = 160.0N. ويسحب Balto أقوى من Astro بقوة مقدارها B = 200.0N، ويسحب Clifford بقوة مقدارها C = 140.0N. عندما يسحب Dug اللعبة بطريقة تجعل قوته تتوازن مع محصلة القوى الثلاث الأخرى، فإن اللعبة لا تتحرك في أي اتجاه. ما مقدار القوة وفي أي اتجاه يجب على Dug سحب اللعبة حتى يحدث هذا التوازن؟

جبر المتجهات - الشكل 2.25 أربعة كلاب تلعب لعبة شد الحبل بلعبة. — جبر المتجهات – الشكل 2.25 أربعة كلاب تلعب لعبة شد الحبل بلعبة.

إستراتيجية الحل

نفترض أن الشرق هو اتجاه المحور x الموجب والشمال هو اتجاه المحور y الموجب. كما في المثال السابق، علينا تحليل القوى الثلاث المحددة A⃗ – (السحب من Astro) و B⃗ (السحب من Balto) و C⃗ (السحب من Clifford) – إلى مكوناتها العددية، ثم إيجاد المكونات العددية للمتجه الناتج (المحصلة) R⃗ =A⃗ +B⃗ +C⃗. عندما توازن قوة السحب D⃗ من Dug خارج هذه المحصلة، يجب أن يعطي مجموع D⃗ و R⃗ المتجه الصفري: D⃗ + R⃗ = 0. هذا يعني أن D⃗ = – R⃗، لذلك يجب أن يكون السحب من Dug عكسيًا للمتجه R⃗.

الحل

لدينا زوايا الاتجاه هي θ_A = −α = – 55، θ_B = 90 – β = 30، وθ_C = 90 + γ = 145، واستبدالها في المعادلة 2.17 يعطي المكونات العددية للقوى الثلاث المعطاة:

\begin{matrix} {\begin{array}{l} A_{x} = A cos θ_{A} = (160.0 N) cos (−55 °) = + 91.8 N \\ A_{y} = A sin θ_{A} = (160.0 N) sin (−55 °) = −131.1 N \end{array} \\ {\begin{array}{l} B_{x} = B cos θ_{B} = (200.0 N) cos 30 ° = + 173.2 N \\ B_{y} = B sin θ_{B} = (200.0 N) sin 30 ° = + 100.0 N \end{array} \\ {\begin{array}{l} C_{x} = C cos θ_{C} = (140.0 N) cos 145 ° = −114.7 N \\ C_{y} = C sin θ_{C} = (140.0 N) sin 145 ° = + 80.3 N \end{array} \end{matrix} .

الآن نحسب المكونات العددية للمتجه المحصلة R⃗ =A⃗ +B⃗ +C⃗

{\begin{matrix} R_{x} = A_{x} + B_{x} + C_{x} = + 91.8 N + 173.2 N - 114.7 N = + 150.3 N \\ R_{y} = A_{y} + B_{y} + C_{y} = −131.1 N + 100.0 N + 80.3 N = + 49.2 N \end{matrix} .

المتجه المعاكس للتوازي مع المحصلة R⃗ هو المتجه D⃗، حيث:

\vec{D} = − \vec{R} = − R_{x} \hat{i} - R_{y} \hat{j} = (−150.3 \hat{i} - 49.2 \hat{j}) N .

مقدار قوة السحب لـ Dug هو:

D = \sqrt{D_{x}^{2} + D_{y}^{2}} = \sqrt{{(−150.3)}^{2} + {(−49.2)}^{2}} N = 158.1 N .

اتجاه قوة سحب Dug هو:

θ = {tan}^{−1} (\frac{D_{y}}{D_{x}}) = {tan}^{−1} (\frac{−49.2 N}{−150.3 N}) = {tan}^{−1} (\frac{49.2}{150.3}) = 18.1 ° .

يسحب Dong في الاتجاه 18.1 درجة جنوب الغرب لأن كلا المكونين سالبين، مما يعني أن متجه السحب يقع في الربع الثالث (الشكل 2.19).

تحقق من فهمك

افترض أن Balto في المثال السابق يترك اللعبة للانتباه إلى أمور أكثر أهمية، لكن Astro وClifford وDug يواصلون اللعب. قوة سحب Astro وClifford للعبة لا تتغير، لكن Dug يجري حول المكان ويسحب اللعبة من مكان مختلف. ما هو مقدار القوة وفي أي اتجاه يجب على Dug سحب اللعبة الآن لموازنة عمليات السحب المجمعة من Clifford وAstro؟ قم بتوضيح هذا الموقف من خلال رسم مخطط متجهات تشير إلى جميع القوى المعنية.

مثال 4: جبر المتجهات

أوجد مقدار المتجه C⃗ الذي يحقق المعادلة:

2 \vec{A} - 6 \vec{B} + 3 \vec{C} = 2 \hat{j}

حيث:

\vec{A} = \hat{i} - 2 \hat{k}

و:

\vec{B} = − \hat{j} + \hat{k} / 2

إستراتيجية الحل

نحل أولاً المعادلة المعطاة للمتجه المجهول C⃗. ثم نستبدل المتجهات A⃗ و B⃗؛ قم بتجميع التعلى طول كل اتجاه من الاتجاهات الثلاثة i^ و j^ و k^؛ وتحديد المكونات العددية C_x و C_y و C_z.

أخيرًا، نعوض في المعادلة 2.21 لإيجاد مقدار المتجه C⃗.

الحل

\begin{matrix} 2 \vec{A} - 6 \vec{B} + 3 \vec{C} & = & 2 \hat{j} \\ 3 \vec{C} & = & 2 \hat{j} - 2 \vec{A} + 6 \vec{B} \\ \vec{C} & = & \frac{2}{3} \hat{j} - \frac{2}{3} \vec{A} + 2 \vec{B} \\ = & \frac{2}{3} \hat{j} - \frac{2}{3} (\hat{i} - 2 \hat{k}) + 2 (− \hat{j} + \frac{\hat{k}}{2}) = \frac{2}{3} \hat{j} - \frac{2}{3} \hat{i} + \frac{4}{3} \hat{k} - 2 \hat{j} + \hat{k} \\ = & - \frac{2}{3} \hat{i} + (\frac{2}{3} - 2) \hat{j} + (\frac{4}{3} + 1) \hat{k} \\ = & - \frac{2}{3} \hat{i} - \frac{4}{3} \hat{j} + \frac{7}{3} \hat{k} . \end{matrix}

المكونات هي: C_x=−2/3, C_y=−4/3, C_z=7/3. والآن نقوم بالتعويض في المعادلة 2.21 والنتيجة هي:

C = \sqrt{C_{x}^{2} + C_{y}^{2} + C_{z}^{2}} = \sqrt{{(−2 / 3)}^{2} + {(− 4 / 3)}^{2} + {(7 / 3)}^{2}} = \sqrt{23 / 3} .

مثال 5: حركة المتزلج

بدءًا من كوخ التزلج، يتجه المتزلج الريفي على الثلج لمسافة 5.0 كم شمالًا، ثم 3.0 كم غربًا، وأخيراً 4.0 كم جنوب غرب قبل أخذ قسط من الراحة. أوجد متجه الإزاحة الإجمالي بالنسبة إلى الكوخ عندما يكون عند نقطة السكون. إلى أي مدى وفي أي اتجاه يجب عليه التزلج من نقطة الاستراحة للعودة مباشرة إلى الكوخ؟

إستراتيجية الحل

نحن نفترض وجود نظام إحداثيات مستطيل مع الأصل عند كوخ التزلج ومع متجه الوحدة i^ يشير إلى الشرق ومتجه الوحدة j^ يشير إلى الشمال. هناك ثلاث حركات نزوح: D⃗ ₁, D⃗ ₂, D⃗ ₃. نحدد مقاديرها على أنها D₁ = 5.0 كيلومتر و D₂ = 3.0 كيلومتر و D₃ = 4.0 كيلومترات. وتحدد اتجاهاتهم الزوايا θ₁ = 90 درجة، θ₂ = 180 درجة، و θ₃ = 180 + 45 = 225 درجة. نحلل كل متجه إزاحة إلى مكوناته العددية ونستبدل المكونات في المعادلة 2.25 للحصول على المكونات العددية لمحصلة الإزاحة الكلية D⃗ من البداية إلى نقطة السكون. في طريق العودة من نقطة الاستراحة إلى الكوخ، تكون الإزاحة B⃗ =−D⃗. أخيرًا، نجد مقدار واتجاه B⃗.

الحل

المكونات العددية لمتجهات الإزاحة هي:

\begin{matrix} {\begin{matrix} D_{1 x} = D_{1} cos θ_{1} = (5.0 km) cos 90 ° = 0 \\ D_{1 y} = D_{1} sin θ_{1} = (5.0 km) sin 90 ° = 5.0 km \end{matrix} \\ {\begin{matrix} D_{2 x} = D_{2} cos θ_{2} = (3.0 km) cos 180 ° = −3.0 km \\ D_{2 y} = D_{2} sin θ_{2} = (3.0 km) sin 180 ° = 0 \end{matrix} \\ {\begin{matrix} D_{3 x} = D_{3} cos θ_{3} = (4.0 km) cos 225 ° = −2.8 km \\ D_{3 y} = D_{3} sin θ_{3} = (4.0 km) sin 225 ° = −2.8 km \end{matrix} \end{matrix} .

المكونات العددية لمتجه الإزاحة الإجمالي هي:

{\begin{matrix} D_{x} = D_{1 x} + D_{2 x} + D_{3 x} = (0 - 3.0 - 2.8) km = −5.8 km \\ D_{y} = D_{1 y} + D_{2 y} + D_{3 y} = (5.0 + 0 - 2.8) km = + 2.2 km \end{matrix} .

ومن ثم، فإن صافي متجه الإزاحة للمتزلج هو:

\vec{D} = D_{x} \hat{i} + D_{y} \hat{j} = (−5.8 \hat{i} + 2.2 \hat{j}) km

وفي طريق العودة إلى الكوخ، تكون إزاحته مساوية لـ

\vec{B} = − \vec{D} = − (−5.8 \hat{i} + 2.2 \hat{j}) km = (5.8 \hat{i} - 2.2 \hat{j}) km

وقيمته العددية هي:

B = \sqrt{B_{x}^{2} + B_{y}^{2}} = \sqrt{{(5.8)}^{2} + {(−2.2)}^{2}} km = 6.2 km

وزاوية اتجاهها هي:

θ = {tan}^{−1} (−2.2 / 5.8) = −20.8 °

لذلك، للعودة إلى الكوخ، يجب أن يسير المتزلج لمسافة 6.2 كم في اتجاه حوالي 21 درجة جنوب شرق.

الدلالة

لاحظ أنه لا حاجة إلى رسم بياني لحل هذه المسألة، أو أي من مسائل جبر المتجهات بالطريقة التحليلية. الرسوم البيانية مطلوبة عند استخدام الطريقة الرسومية في الحل. ومع ذلك، يمكننا التحقق مما إذا كان حلنا منطقيًا من خلال رسمه، وهي خطوة أخيرة مفيدة في حل أي مسألة من مسائل جبر المتجهات.

مثال 6: إزاحة عداء ببطء

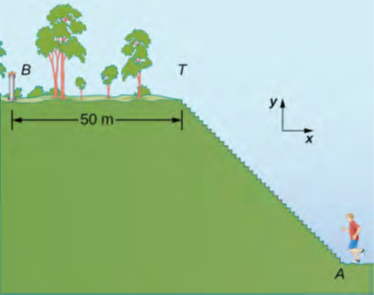
يركض عداء ببطء في رحلة من 200 درجات سلالم متطابقة إلى قمة تل ثم يمتد على طول قمة التل مسافة 50.0 متر قبل أن يتوقف عند نافورة مياه الشرب (الشكل 2.26). متجه الإزاحة من النقطة A أسفل الدرجات إلى النقطة B عند النافورة هو:

{\vec{D}}_{A B} = (−90.0 \hat{i} + 30.0 \hat{j}) m

ما هو ارتفاع وعرض كل خطوة في الرحلة؟ ما هي المسافة الفعلية التي يقطعها العداء ببطء؟ إذا صنع حلقة وعاد إلى النقطة A، فما هي محصلة صافي متجه الإزاحة؟

جبر المتجهات - شكل 2.26 عداء ببطء يجري مجموعة من الدرجات. — جبر المتجهات – شكل 2.26 عداء ببطء يجري مجموعة من الدرجات.

إستراتيجية الحل

متجه الإزاحة D⃗ _AB هو المجموع الاتجاهي لمتجه إزاحة العداء D_AT على طول الدرج (من النقطة A في أسفل الدرج إلى النقطة T في أعلى الدرج) ومتجه الإزاحة D_TB أعلى التل (من النقطة A في أعلى الدرج إلى النافورة عند النقطة T). علينا إيجاد المركبين الأفقي والعمودي لـ D_AT. إذا كان لكل خطوة عرض w وارتفاع h، فيجب أن يبلغ طول المكون الأفقي لـ D_AT مقدار 200w ويجب أن يبلغ طول المكون الرأسي 200h. المسافة الفعلية التي يقطعها العداء هي مجموع المسافة التي يقطعها في صعود الدرج مع المسافة البالغة 50.0 متر التي يقطعها على طول قمة التل.

الحل

في نظام الإحداثيات الموضح في الشكل 2.26، يكون متجه إزاحة العداء أعلى التل هو D_TB = (50.0 m) i^. متجه الإزاحة الصافي له هو:

{\vec{D}}_{A B} = {\vec{D}}_{A T} + {\vec{D}}_{T B} .

لذلك، فإن متجه إزاحته D_TB على طول الدرج هو:

\begin{array}{l} {\vec{D}}_{A T} & = {\vec{D}}_{A B} - {\vec{D}}_{T B} = (−90.0 \hat{i} + 30.0 \hat{j}) m - (−50.0 m) \hat{i} = [(−90.0 + 50.0) \hat{i} + 30.0 \hat{j})] m \\ = (−40.0 \hat{i} + 30.0 \hat{j}) m . \end{array}

أي أن مكوناته العددية هي:

D_{A T x} = −40.0 m

D_{A T y} = 30.0 m

لذلك، يجب أن يكون لدينا:

200 w = | - 40.0 | m and 200 h = 30.0 m .

ومن ثم، فإن عرض الخطوة هو w = 40.0 / 200 = 0.2 m أو 20 سم، وارتفاع الخطوة h = 30.0 / 200 = 0.15 m أو 15 سم. والمسافة التي يقطعها العداء على طول الدرج هي:

D_{A T} = \sqrt{D_{A T x}^{2} + D_{A T y}^{2}} = \sqrt{{(−40.0)}^{2} + {(30.0)}^{2}} m = 50.0 m .

وبالتالي، فإن المسافة الفعلية التي يقطعها هي D_AT + D_TB وهي تساوي 50.0 متر + 50.0 متر = 100.0 متر.

عندما يصنع حلقة ويعود من النافورة إلى موضعه الأولي عند النقطة A، تكون المسافة الإجمالية التي يقطعها ضعف هذه المسافة، أو 200.0 متر. ومع ذلك، فإن صافي متجه الإزاحة الخاص به هو صفر، لأنه عندما يكون موضعه النهائي هو نفسه موضعه الأولي، فإن المكونات القياسية لصافي متجه الإزاحة تكون صفرًا (المعادلة 2.13).

متجه الوحدة في جبر المتجهات

في جبر المتجهات وفي كثير من المواقف الفيزيائية نحتاج غالبًا إلى معرفة اتجاه المتجه. على سبيل المثال، قد نرغب في معرفة اتجاه متجه المجال المغناطيسي عند نقطة ما أو اتجاه حركة الجسم. لقد قلنا بالفعل أن الاتجاه يتم توفيره بواسطة متجه وحدة Unit Vector، وهو كيان بلا أبعاد – أي أنه لا يحتوي على وحدات فيزيائية مرتبطة به. عندما يقع المتجه المعني على أحد المحاور في نظام الإحداثيات الديكارتية، تكون الإجابة بسيطة، لأن متجه الوحدة الخاص به يكون إما موازيًا أو معاكسًا لاتجاه متجه الوحدة للمحور. على سبيل المثال، اتجاه المتجه d = −5 m i^ هو متجه الوحدة d^ = −i^. القاعدة العامة لإيجاد متجه الوحدة V^ لاتجاه أي متجه V هي تقسيمه على مقداره V:

\hat{V} = \frac{\vec{V}}{V} .

(2.26)

نرى من هذا التعبير أن متجه الوحدة في الاتجاه بلا أبعاد لأن البسط والمقام في المعادلة 2.26 لهما نفس الوحدة الفيزيائية. بهذه الطريقة، تسمح لنا المعادلة 2.26 بالتعبير عن متجه الوحدة للاتجاه بدلالة متجهات الوحدة للمحاور. المثال التالي يوضح هذا المبدأ.

مثال 7: متجه الوحدة للاتجاه

إذا كان متجه السرعة للقافلة العسكرية في المثال رقم 1 هو:

\vec{v} = (4.000 \hat{i} + 3.000 \hat{j} + 0.100 \hat{k}) km / h

فما متجه الوحدة لاتجاه حركتها؟

إستراتيجية الحل

متجه الوحدة لاتجاه حركة القافلة هو متجه الوحدة v^ الذي يوازي متجه السرعة. يتم الحصول على متجه الوحدة بقسمة المتجه على مقداره أو قيمته، وفقًا للمعادلة 2.26.

الحل

مقدار المتجه v هو:

v = \sqrt{v_{x}^{2} + v_{y}^{2} + v_{z}^{2}} = \sqrt{{4.000}^{2} + {3.000}^{2} + {0.100}^{2}} km / h = 5.001 km / h .

للحصول على متجه الوحدة v^، اقسم المتجه v → على مقداره:

\begin{matrix} \hat{v} & = \frac{\vec{v}}{v} = \frac{(4.000 \hat{i} + 3.000 \hat{j} + 0.100 \hat{k}) km / h}{5.001 km / h} \\ = \frac{(4.000 \hat{i} + 3.000 \hat{j} + 0.100 \hat{k})}{5.001} \\ = \frac{4.000}{5.001} \hat{i} + \frac{3.000}{5.001} \hat{j} + \frac{0.100}{5.001} \hat{k} \\ = (79.98 \hat{i} + 59.99 \hat{j} + 2.00 \hat{k}) \times 10^{−2} . \end{matrix}

الدلالة

لاحظ أنه عند استخدام الطريقة التحليلية مع الآلة الحاسبة، يُنصح بإجراء الحسابات الخاصة بك إلى ثلاثة منازل عشرية على الأقل ثم تقريب الإجابة النهائية إلى العدد المطلوب من الأرقام المهمة، وهي الطريقة التي أجرينا بها الحسابات في هذا المثال. إذا قمت بتقريب إجابتك الجزئية في وقت مبكر جدًا، فإنك تخاطر بحدوث خطأ رقمي كبير في إجابتك النهائية، وقد تكون بعيدة عن الإجابة الدقيقة أو عن القيمة التي تم قياسها في التجربة.

تحقق من فهمك

تحقق من أن المتجه v^ الذي تم الحصول عليه في المثال السابق هو في الواقع متجه وحدة عن طريق حساب مقداره. إذا كانت القافلة في المثال الأول تتحرك عبر أرض صحراوية مسطحة – أي إذا كان المكون الثالث من سرعتها صفرًا – فما متجه الوحدة لاتجاه حركتها؟ وما هو الاتجاه الجغرافي الذي يمثله؟

المصدر

موسوعة الفيزياء العامة، ترجمة وإعداد: د. م. مصطفى عبيد، مركز البحوث والدراسات متعدد التخصصات، 2022.
كتاب الفيزياء للجامعات، صموئيل جيه لينغ، جامعة ولاية ترومان، د. جيف ساني، جامعة لويولا ماريماونت ويليام مويبس.