تطبيقات قوانين نيوتن
نمت شعبية سباقات السيارات في السنوات الأخيرة. عندما تتحرك كل سيارة في مسار منحني حول المنعطف، تدور عجلاتها أيضًا بسرعة. تكمل العجلات العديد من الدورات بينما تصنع السيارة جزءًا واحدًا فقط (قوس دائري). كيف يمكننا وصف السرعات والتسارع والقوى المعنية؟ ما هي القوة التي تمنع سيارة السباق من الدوران، واصطدامها بالجدار المجاور للمسار؟ ما الذي يمد هذه القوة؟ لماذا يتم حني المسار؟ نجيب على كل هذه الأسئلة في هذا الفصل الذي يتناول تطبيقات قوانين نيوتن في الحياة العملية، بينما نوسع نظرنا في قوانين نيوتن للحركة.

الشكل 6.1 سيارات السباق تتسابق في سباق التقسيم الوطني الكبير في آيوا سبيدواي في مايو 2015. تصل السيارات غالبًا إلى سرعة 200 ميل في الساعة (320 كم / ساعة). (المصدر: بواسطة إريك شنايدر / البحرية الأمريكية)
مخطط الفصل
- 6.1 حل المسائل باستخدام قوانين نيوتن
- 6.2 الاحتكاك
- 6.3 قوة الجاذبية
- 6.4 قوة السحب وسرعة المحطة
حل المسائل باستخدام قوانين نيوتن
أهداف التعلم
بنهاية هذا القسم، ستكون قادرًا على:
- تطبيق تقنيات حل المسائل لإيجاد الكميات في أنظمة القوى الأكثر تعقيدًا
- استخدم مفاهيم من علم الحركة لحل المسائل باستخدام قوانين نيوتن للحركة
- حل مسائل الاتزان الأكثر تعقيدًا في تطبيقات قوانين نيوتن للحركة
- حل مسائل التسارع الأكثر تعقيدًا ضمن تطبيقات قوانين نيوتن
- تطبيق حساب التفاضل والتكامل على مسائل الديناميكا الأكثر تقدمًا
إن النجاح في حل المسائل ضروري لفهم وتطبيق المبادئ الفيزيائية. لقد طورنا نمطًا للتحليل ووضع الحلول للمسائل التي تتضمن قوانين نيوتن في قوانين نيوتن للحركة؛ في هذا الفصل، نواصل مناقشة هذه الاستراتيجيات والتطبيق العملي خطوة بخطوة.
المحتويات
استراتيجيات حل المسائل
نتبع هنا أساسيات حل المسائل المقدمة مسبقًا في هذا الكتاب، لكننا نؤكد على استراتيجيات محددة مفيدة في تطبيق قوانين نيوتن للحركة. بمجرد تحديد المبادئ الفيزيائية التي تنطوي عليها المسألة وتحديد أنها تتضمن قوانين نيوتن للحركة، يمكنك تطبيق هذه الخطوات لإيجاد الحل. تعزز هذه التقنيات أيضًا المفاهيم المفيدة في العديد من مجالات الفيزياء الأخرى. تم ذكر العديد من استراتيجيات حل المشكلات بشكل صريح في الأمثلة العملية، لذا يجب أن تعزز الأساليب التالية المهارات التي بدأت بالفعل في تطويرها.
استراتيجية حل المسائل وتطبيق قوانين نيوتن للحركة
- حدد المبادئ الفيزيائية المتضمنة من خلال سرد المعطيات والكميات المطلوب حسابها.
- ارسم الموقف باستخدام الأسهم لتمثيل جميع القوى.
- حدد نظام الاهتمام. والنتيجة هي رسم تخطيطي للجسم الحر ضروري لحل المسألة.
- طبق قانون نيوتن الثاني لحل المسألة. إذا لزم الأمر، قم بتطبيق المعادلات الحركية المناسبة من الفصل الخاص بالحركة في خط مستقيم.
- تحقق من الحل لمعرفة ما إذا كان معقولًا.
دعنا نطبق استراتيجية حل المسال هذه على التحدي المتمثل في رفع بيانو كبير إلى شقة من الطابق الثاني. بمجرد أن نحدد أن قوانين نيوتن للحركة متضمنة (إذا كانت المسألة تتعلق بالقوى)، فمن المهم بشكل خاص رسم مخطط دقيق للموقف. يظهر هذا الرسم في الشكل 6.2 (أ). بعد ذلك، كما في الشكل 6.2 (ب)، يمكننا تمثيل جميع القوى بأسهم. متى وجدت معلومات كافية، فمن الأفضل تسمية هذه الأسهم بعناية وجعل طول واتجاه كل منها يتوافق مع القوة الممثلة.
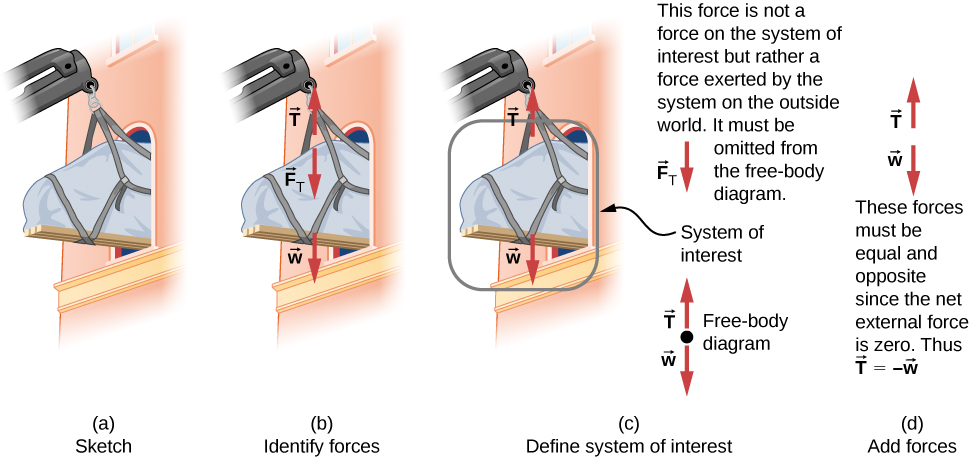
الشكل 6.2 (أ) يتم رفع بيانو كبير إلى شقة من الطابق الثاني. (ب) تُستخدم الأسهم لتمثيل جميع القوى: T⃗ هو الشد في الحبل فوق البيانو، F⃗ T هي القوة التي يبذلها البيانو على الحبل، وw⃗ هو وزن البيانو. يُفترض أن جميع القوى الأخرى، مثل دفع النسيم، مهملة. (ج) لنفترض أننا حصلنا على كتلة البيانو وطُلب منا إيجاد الشد في الحبل. نحدد نظام الاهتمام كما هو موضح ونرسم مخطط الجسم الحر. الآن لم تعد F⃗ T معروضة، لأنها ليست قوة تعمل على نظام الاهتمام؛ بدلاً من ذلك، تعمل F⃗ T على العالم الخارجي. (د) إظهار الأسهم فقط، يتم استخدام طريقة الجمع من الرأس إلى الذيل. من الواضح أنه إذا كان البيانو ثابتًا، T⃗ = −w⃗.
كما هو الحال مع معظم المسائل، نحتاج بعد ذلك إلى تحديد ما يجب تحديده وما هو معروف أو يمكن استنتاجه من المسألة كما هو مذكور، أي إعداد قائمة بالمعلومات المعروفة والمجهولة. من الأهمية بمكان تحديد نظام الاهتمام، نظرًا لأن قانون نيوتن الثاني يتضمن قوى خارجية فقط. يمكننا بعد ذلك تحديد القوى الخارجية والداخلية، وهي خطوة ضرورية لاستخدام قانون نيوتن الثاني. (انظر الشكل 6.2 (ج)).
يمكن استخدام قانون نيوتن الثالث لتحديد ما إذا كانت القوى تمارس بين مكونات النظام (داخلي) أو بين النظام وشيء خارجي (خارجي). كما هو موضح في قوانين الحركة لنيوتن، يعتمد نظام الاهتمام على السؤال الذي نحتاج إلى الإجابة عليه. فقط القوى الموضحة في مخططات الجسم الحر، وليس التسارع أو السرعة. لقد رسمنا العديد من مخططات الجسم الحر في الأمثلة السابقة. يوضح الشكل 6.2 (ج) مخطط الجسم الحر لنظام الاهتمام. لاحظ أنه لا توجد قوى داخلية معروضة في مخطط الجسم الحر.
بمجرد رسم مخطط الجسم الحر، نطبق قانون نيوتن الثاني. يتم ذلك في الشكل 6.2 (د) لحالة معينة. بشكل عام، بمجرد تحديد القوى الخارجية بوضوح في مخططات الجسم الحر، يجب أن تكون مهمة مباشرة لوضعها في شكل معادلة وحلها بإيجاد المجهول، كما حدث في جميع الأمثلة السابقة. إذا كانت المسألة أحادية البعد – أي إذا كانت جميع القوى متوازية – فيمكن عندئذٍ معالجة القوى جبريًا. إذا كانت المسألة ثنائية الأبعاد، فيجب تقسيمها إلى زوج من المسائل أحادية البعد. نقوم بذلك عن طريق إسقاط متجهات القوة على مجموعة من المحاور المختارة للراحة.
كما رأينا في الأمثلة السابقة، يمكن أن يؤدي اختيار المحاور إلى تبسيط المسألة. على سبيل المثال، عندما يكون هناك منحدر، تكون مجموعة المحاور ذات المحور الموازي للانحدار والآخر العمودي عليه هي الأكثر ملاءمة. من الملائم دائمًا جعل أحد المحاور موازٍ لاتجاه الحركة، إذا كان ذلك معروفًا. بشكل عام، ما عليك سوى كتابة قانون نيوتن الثاني في المكونات على طول الاتجاهات المختلفة. بعد ذلك، لديك المعادلات التالية:
(على سبيل المثال، إذا كان النظام يتسارع أفقيًا، فيمكنك حينئذٍ تعيين ay = 0) نحتاج إلى هذه المعلومات لتحديد القوى غير المعروفة المؤثرة على النظام.
كما هو الحال دائمًا، يجب أن نتحقق من الحل. في بعض الحالات، من السهل معرفة ما إذا كان الحل معقولًا. على سبيل المثال، من المعقول أن نجد أن الاحتكاك يتسبب في انزلاق جسم ما إلى أسفل منحدر أبطأ مما هو عليه في حالة عدم وجود احتكاك. في الممارسة العملية، يتطور الحدس تدريجيًا من خلال حل المسائل. ومع الخبرة، يصبح من الأسهل بشكل تدريجي الحكم على ما إذا كانت الإجابة معقولة. هناك طريقة أخرى للتحقق من الحل وهي فحص الوحدات. إذا أردنا إيجاد القوة وانتهى بنا الأمر بوحدات ملليمترات في الثانية، فإننا قد ارتكبنا خطأ.
هناك العديد من التطبيقات المثيرة للاهتمام لقوانين نيوتن للحركة، يتم تقديم عدد قليل منها في هذا القسم. تعمل هذه أيضًا على توضيح بعض التفاصيل الدقيقة للفيزياء والمساعدة في بناء مهارات حل المسائل. ننظر أولاً إلى المسائل التي تنطوي على توازن الجسيمات، والتي تستفيد من قانون نيوتن الأول، ثم ننظر في تسارع الجسيمات، والتي تتضمن قانون نيوتن الثاني.
توازن الجسيمات
تذكر أن الجسيم الذي يكون في حالة التوازن هو الذي تتوازن فيه القوى الخارجية. يتضمن التوازن الثابت أجسامًا في حالة سكون، ويتضمن التوازن الديناميكي كائنات متحركة بدون تسارع، ولكن من المهم أن نتذكر أن هذه الشروط نسبية. على سبيل المثال، قد يكون الجسم في حالة سكون عند النظر إليه من إطارنا المرجعي، ولكن نفس الكائن قد يبدو أنه يتحرك عندما ينظر إليه شخص يتحرك بسرعة ثابتة (مثال: النظر إلى الكرسي الذي تجلس عليه داخل الطائرة، هو في حالة سكون بالنسبة لك، ولكنه في حالة حركة بالنسبة لشخص ينظر إليه من سطح الأرض). نحن الآن نستفيد من المعرفة المكتسبة في تطبيقات قوانين نيوتن للحركة، فيما يتعلق بأنواع القوى المختلفة واستخدام مخططات الجسم الحر، لحل مسائل إضافية في توازن الجسيمات.
مثال 6.1: قوى الشد المختلفة بزوايا مختلفة
ضع في اعتبارك إشارة المرور (كتلة 15.0 كجم) معلقة من سلكين كما هو موضح في الشكل 6.3. أوجد الشد في كل سلك، مع إهمال كتل الأسلاك.
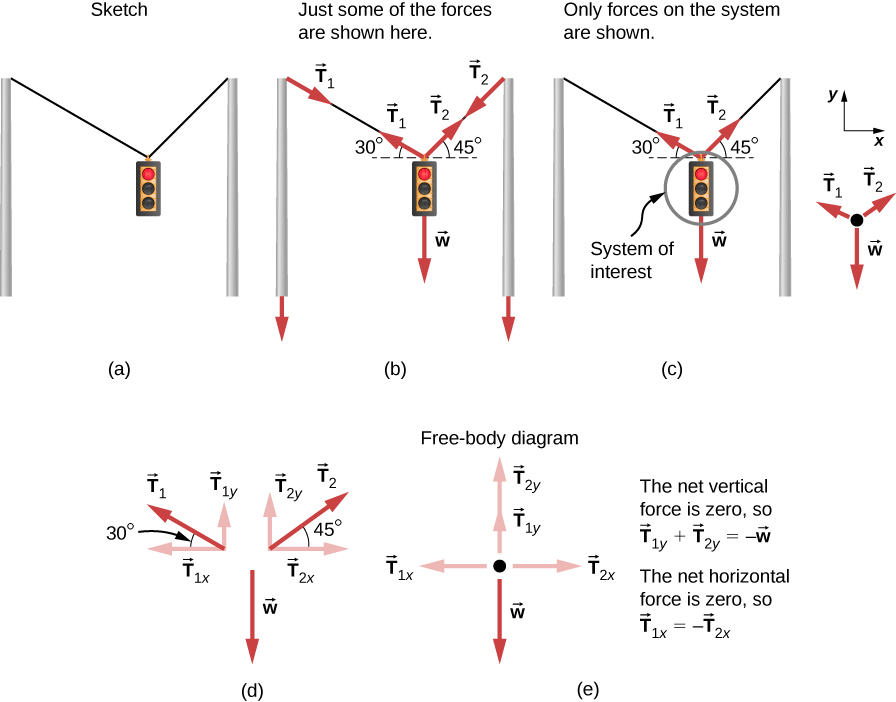
الشكل 6.3: يتم تعليق إشارة المرور من سلكين. (ب) بعض القوى المشاركة (ج) تظهر هنا فقط القوى المؤثرة على النظام. يظهر أيضًا مخطط الجسم الحر لإشارة المرور. (د) القوى المسقطة على المحاور الرأسية (ص) والأفقية (س). يجب إلغاء المكونات الأفقية للشد، ويجب أن يتساوى مجموع المكونات الرأسية للشد مع وزن إشارة المرور. (هـ) يوضح مخطط الجسم الحر القوى الرأسية والأفقية التي تعمل على إشارة المرور.
استراتيجية الحل
نظام الاهتمام هو إشارة المرور، ويظهر مخطط الجسم الحر في الشكل 6.3 (ج). القوى الثلاث المعنية ليست متوازية، ولذلك يجب إسقاطها على نظام إحداثيات. يحتوي نظام الإحداثيات الأكثر ملاءمة على محور واحد رأسي وآخر أفقي، وتظهر إسقاطات المتجهات عليه في الشكل 6.3 (د). هناك نوعان من المجهول في هذه المسألة (T1 و T2)، لذلك هناك حاجة إلى معادلتين لإيجادهما. تأتي هاتان المعادلتان من تطبيق قانون نيوتن الثاني على طول المحورين الرأسي والأفقي، مع ملاحظة أن صافي القوة الخارجية يساوي صفرًا على طول كل محور لأن التسارع يساوي صفرًا.
الحل
فكر أولاً في المحور الأفقي أو المحور السيني:
Fnetx =T2x + T1x = 0
وهكذا، كما قد تتوقع،
|T1x|=|T2x|
هذا يعطينا العلاقة التالية:
T1 cos 30 = T2 cos 45
وهكذا،
T2 = 1.225 T1
لاحظ أن T1 وT2 ليسا متساويين في هذه الحالة لأن الزاويتين على كلا الجانبين غير متساويتين. من المعقول أن يكون T2 أكبر من T1 لأنه يتم إجراؤه بشكل أقرب للاتجاه العمودي أكثر من T1.
الآن ضع في اعتبارك مكونات القوة على طول المحور الرأسي أو المحور الصادي:
Fnety =T1y + T2y – w = 0
هذا يعني
T1y + T2y = w
يعطي استبدال التعبيرات للمكونات الرأسية
T1 sin 30 + T2 sin 45 = w
هناك عدد اثنين من المجاهيل في هذه المعادلة، ولكن عند استبدال التعبير T2 بدلالة T1 يقلل ذلك من عدد هذه المجاهيل ويجعل المعادلة فيها مجهول واحد كما يلي:
T1 (0.500) + (1.225T1) (0.707) = w = mg
الذي ينتج لنا:
1.366 T1=(15.0kg)(9.80 m/s2)
حل هذه المعادلة الأخيرة يعطي مقدار T1
T1 = 108 N
أخيرًا، نجد مقدار T2 باستخدام العلاقة، T2 = 1.225 T1، الموجودة أعلاه. هكذا نحصل على:
T2 = 132 N
الدلالة
سيكون كلا الشدين أكبر إذا كان كلا السلكين أفقيًا، وسيكونان متساويين إذا وفقط إذا كانت الزوايا على كلا الجانبين متطابقة (كما كانت في المثال السابق للرجل الذي يمشي على الحبل المشدود في قوانين نيوتن للحركة).
تسريع الجسيمات
لقد قدمنا مجموعة متنوعة من الأمثلة للجسيمات في حالة التوازن. نوجه انتباهنا الآن إلى مسائل تسارع الجسيمات، والتي تنتج عن قوة محصلة غير صفرية. ارجع مرة أخرى إلى الخطوات الواردة في بداية هذا القسم، ولاحظ كيف يتم تطبيقها على الأمثلة التالية.
مثال 6.2: قوة السحب على البارجة
زورقان يدفعان على بارجة بزوايا مختلفة (الشكل 6.4). يمارس الزورق الأول قوة مقدارها 2.7 × 105 نيوتن في الاتجاه X، ويؤثر الزورق الثاني بقوة مقدارها 3.6 × 105 نيوتن في الاتجاه Y. كتلة البارجة 5.0 × 106 كجم وتسارعها 7.5 × 10−2 م / ث2 في الاتجاه الموضح. ما هي قوة سحب الماء على البارجة التي تقاوم الحركة؟ (ملاحظة: قوة السحب هي قوة احتكاك ناتجة عن السوائل، مثل الهواء أو الماء. وتعارض قوة السحب حركة الجسم. نظرًا لأن البارجة مسطحة القاع، يمكننا أن نفترض أن قوة السحب في الاتجاه المعاكس للحركة من البارجة).
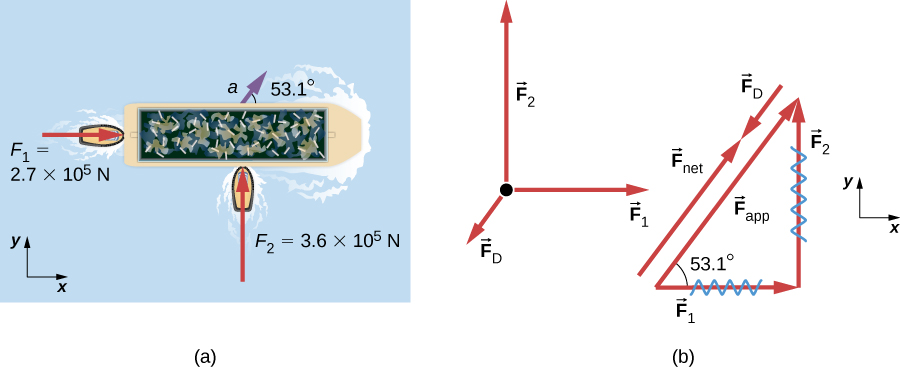
الشكل 6.4 (أ) منظر من أعلى لزورقين يضغطان على بارجة. (ب) يحتوي مخطط الجسم الحر للبارجة على القوى المؤثرة في مستوى الماء فقط. إنه يغفل القوتين الرأسيتين – يلغي وزن البارجة وقوة الطفو للمياه الداعمة لها ولا تظهران. لاحظ أن تطبيق F⃗ هو إجمالي القوة المطبقة على الزوارق.
استراتيجية الحل
ترد اتجاهات ومقادير التسارع والقوى المطبقة في الشكل 6.4 (أ). نحدد القوة الإجمالية للزوارق المؤثرة على البارجة على أنها F⃗app لذلك يكون:
F⃗app = F⃗1 + F⃗2
سحب الماء F⃗D في الاتجاه المعاكس لاتجاه حركة القارب؛ وبالتالي تعمل هذه القوة ضد F⃗app، كما هو موضح في الرسم التخطيطي للجسم الحر في الشكل 6.4 (ب). نظام الاهتمام هنا هو البارجة، حيث يتم إعطاء القوى الموجودة عليها بالإضافة إلى تسارعها. نظرًا لأن القوى المطبقة متعامدة، فإن المحورين x وy في نفس اتجاه F⃗1 و F⃗2. تصبح المسألة بسرعة مسألة أحادية البعد على طول اتجاه F⃗app، نظرًا لأن الاحتكاك في الاتجاه المعاكس لـ F⃗app. تتمثل استراتيجيتنا في إيجاد مقدار واتجاه صافي تطبيق القوة المؤثرة F⃗ ثم تطبيق قانون نيوتن الثاني للحل وإيجاد قوة السحب F⃗D.
الحل
نظرًا لأن Fx و Fy متعامدان، يمكننا إيجاد مقدار واتجاه F⃗app مباشرةً. أولاً، يتم إعطاء المقدار الناتج بواسطة نظرية فيثاغورس كما يلي:
Fapp= √(F12 + F22)
√( (2.7×105N)2 + (3.6×105N)2 )= 4.5×105 N
إيجاد الزاوية:
θ = tan − 1 (F2 / F1) = tan − 1 (3.6 × 105 N/2.7 × 105N) = 53.1
من قانون نيوتن الأول، نعلم أن هذا هو نفس اتجاه التسارع. نعلم أيضًا أن F⃗D في الاتجاه المعاكس لـ F⃗app، لأنها تعمل على إبطاء التسارع. لذلك، فإن صافي القوة الخارجية في نفس اتجاه F⃗app، لكن حجمها أقل قليلاً من F⃗app. المسألة الآن ذات بعد واحد. من مخطط الجسم الحر، يمكننا أن نرى أن:
Fnet = Fapp – FD
ومع ذلك، ينص قانون نيوتن الثاني على أن:
Fnet = m a
وهكذا يكون:
Fapp – FD = m a
يمكن حل هذه المعادلة من أجل إيجاد مقدار قوة سحب الماء FD بدلالة الكميات المعروفة:
FD = Fapp – m a
وبالتعويض عن القيم المعروفة ينتج لنا:
FD=(4.5×105N)−(5.0×106kg)(7.5×10−2m/s2)=7.5×104N.FD=(4.5×105N)−(5.0×106kg)(7.5×10−2m/s2)=7.5×104N.
تم بالفعل تحديد اتجاه F⃗ D ليكون في الاتجاه المعاكس لاتجاه F⃗app، أو بزاوية 53 درجة جنوب الغرب.
الدلالة
الأرقام المستخدمة في هذا المثال معقولة لبارجة كبيرة إلى حد ما. من المؤكد أنه من الصعب الحصول على تسارعات أكبر باستخدام القاطرات، كما أن السرعات الصغيرة مرغوبة لتجنب تشغيل البارجة في الأرصفة. يعتبر السحب صغيرًا نسبيًا بالنسبة لهيكل جيد التصميم بسرعات منخفضة، بما يتوافق مع الإجابة على هذا المثال، حيث يكون FD أقل من 1/600 من وزن البارجة.
في قوانين الحركة لنيوتن، ناقشنا القوة العادية، وهي قوة تلامس تعمل بشكل طبيعي على السطح بحيث لا يكون للجسم تسارع عمودي على السطح. ميزان الحمام هو مثال ممتاز للقوة الطبيعية التي تؤثر على الجسم. يوفر قراءة كمية لمقدار ما يجب أن يدفع لأعلى لدعم وزن الجسم. ولكن هل يمكنك أن تتنبأ بما قد تراه على قرص ميزان الحمام إذا وقفت عليه أثناء ركوب المصعد؟ هل سترى قيمة أكبر من وزنك عند بدء تشغيل المصعد؟ ماذا عن عندما يتحرك المصعد لأعلى بسرعة ثابتة؟ حاول أن تخمن قبل قراءة المثال التالي.
مثال 6.3: ماذا يقرأ الميزان في المصعد؟
يوضح الشكل 6.5 رجلاً وزنه 75.0 كجم (وزنه حوالي 165 رطلاً) يقف على ميزان حمام في مصعد. احسب قراءة الميزان: (أ) إذا تسارع المصعد لأعلى بمعدل 1.20 م / ث 2، و(ب) إذا تحرك المصعد لأعلى بسرعة ثابتة تبلغ 1 م / ث.
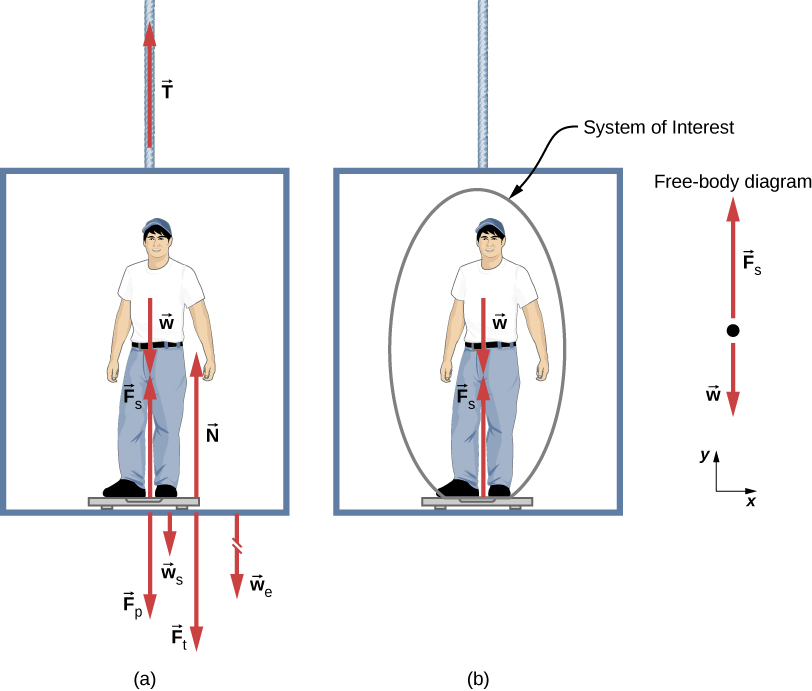
الشكل 6.5 (أ) القوى المختلفة التي تعمل عندما يقف شخص على ميزان حمام في مصعد. تكون الأسهم صحيحة تقريبًا عندما يكون المصعد يتسارع لأعلى – تمثل الأسهم المكسورة قوى كبيرة جدًا بحيث لا يمكن رسمها على نطاق واسع. T⃗ هو الشد في الكابل الداعم، w⃗ هو وزن الشخص، w⃗ s هو وزن الميزان، w⃗ e هو وزن المصعد، F⃗s هي قوة الميزان على الشخص، F⃗p هي قوة الشخص على الميزان، F⃗t هي قوة الميزان على أرضية المصعد، و N⃗ هي قوة الأرضية لأعلى على الميزان. (ب) يوضح مخطط الجسم الحر فقط القوى الخارجية التي تعمل على النظام المعين للاهتمام – الشخص – وهو الرسم البياني الذي نستخدمه لحل المسألة.
استراتيجية الحل
إذا كان الميزان عند السكون دقيقًا، فإن قراءته تساوي F⃗p، مقدار القوة التي يبذلها الشخص لأسفل عليه. يوضح الشكل 6.5 (أ) القوى العديدة التي تعمل على المصعد والميزان والشخص. إنه يجعل هذه المشكلة أحادية البعد تبدو أكثر صعوبة مما لو تم اختيار الشخص ليكون النظام محل الاهتمام ورسم مخطط الجسم الحر، كما في الشكل 6.5 (ب). يمكن أن ينتج عن تحليل مخطط الجسم الحر باستخدام قوانين نيوتن إجابات لكل من الشكل 6.5 (أ) و(ب) من هذا المثال، بالإضافة إلى بعض الأسئلة الأخرى التي قد تطرأ. القوى الوحيدة المؤثرة على الشخص هي وزنه والقوة الصاعدة للميزان Fs. وفقًا لقانون نيوتن الثالث، F⃗p و F⃗s متساويان في المقدار ومتعاكستان في الاتجاه، لذلك نحتاج إلى إيجاد Fs لإيجاد ما يقرأه الميزان. يمكننا القيام بذلك، كالعادة، من خلال تطبيق قانون نيوتن الثاني:
F⃗ net = m a⃗
من مخطط الجسم الحر، نرى أن F⃗ net = F⃗ s − w⃗، إذن لدينا:
Fs – w = m a
يعطينا الحل بالنسبة لـ Fs معادلة واحدة بمجهول واحد فقط:
Fs = m a + w
أو، لأن w = mg، فيكون ببساطة لدينا:
Fs = m a + m g
لم يتم عمل أي افتراضات حول التسارع، لذلك يجب أن يكون هذا الحل صالحًا لمجموعة متنوعة من التسارع بالإضافة إلى تلك الموجودة في هذه الحالة. (ملاحظة: نحن ندرس الحالة التي يكون فيها المصعد يتسارع لأعلى. إذا كان المصعد يتسارع لأسفل، فإن قانون نيوتن الثاني يصبح Fs − w = −ma).
الحل
لدينا التسارع a = 1.20m/s2 ، لذا يكون:
Fs=(75.0 kg)(9.80 m/s2)+(75.0 kg)(1.20 m/s2)
وهذا يعطينا:
Fs = 825 Newton
الآن، ماذا يحدث عندما يصل المصعد إلى سرعة تصاعدية ثابتة؟ هل سيظل الميزان يقرأ أكثر من وزنه؟ لأي سرعة ثابتة – أعلى أو أسفل أو ساكنًا – يكون التسارع صفرًا لأن: a = Δv/Δt و Δv = 0. وهكذا يكون:
Fs = m a + m g = 0 + mg
أو
Fs = (75.0kg)(9.80m/s2)
Fs = 735 N
الدلالة
تبلغ قراءة الميزان في الشكل 6.5 (أ) حوالي 185 رطلاً. ما الذي كان سيقرأه الميزان إذا كانت السرعة ثابتة؟ نظرًا لأن تسارعه سيكون صفرًا، فإن قوة الميزان ستكون مساوية لوزنه:
Fnet = m a = 0 = Fs − w
Fs = w = m g
Fs = (75.0kg)(9.80m/s2) = 735 N
وبالتالي، فإن قراءة الميزان في المصعد أكبر من وزنه البالغ 735 نيوتن (165 رطلاً). هذا يعني أن الميزان يدفع الشخص بقوة أكبر من وزنه، كما يجب أن تسرعه صعودًا. من الواضح أنه كلما زاد تسارع المصعد، زادت قراءة الميزان، بما يتوافق مع ما تشعر به في المصاعد المتسارعة بسرعة مقابل المصاعد المتسارعة ببطء. في الشكل 6.5 (ب)، تبلغ قراءة الميزان 735 نيوتن، وهو ما يساوي وزن الشخص. هذا هو الحال عندما يكون للمصعد سرعة ثابتة – يتحرك لأعلى أو لأسفل أو ساكنًا.
تحقق من فهمك 6.1
الآن احسب قراءة الميزان عندما يتسارع المصعد للأسفل بمعدل 1.20 م/ث2.
ينطبق حل المثال السابق أيضًا على مصعد يتسارع إلى أسفل، كما هو مذكور. عندما يتسارع المصعد لأسفل، تكون a سالبة، وتكون قراءة الميزان أقل من وزن الشخص. إذا تم الوصول إلى سرعة تنازلية ثابتة، فإن قراءة الميزان مرة أخرى تصبح مساوية لوزن الشخص. إذا كان المصعد في حالة سقوط حر ويتسارع لأسفل عند تسارع مقداره g، فإن قراءة الميزان تكون صفرًا، ويبدو عندئذٍ أن الشخص عديم الوزن.
مثال 6.4: كتلتان متصلتان بخيط عبر بكرة
يوضح الشكل 6.6 كتلة كتلتها m1 على سطح أفقي عديم الاحتكاك. يتم سحبها بواسطة خيط خفيف يمر فوق بكرة عديمة الاحتكاك وعديمة الكتلة. الطرف الآخر من الخيط متصل بكتلة كتلتها m2. أوجد تسارع الكتل وشد الخيط بدلالة m1 و m2 و g.
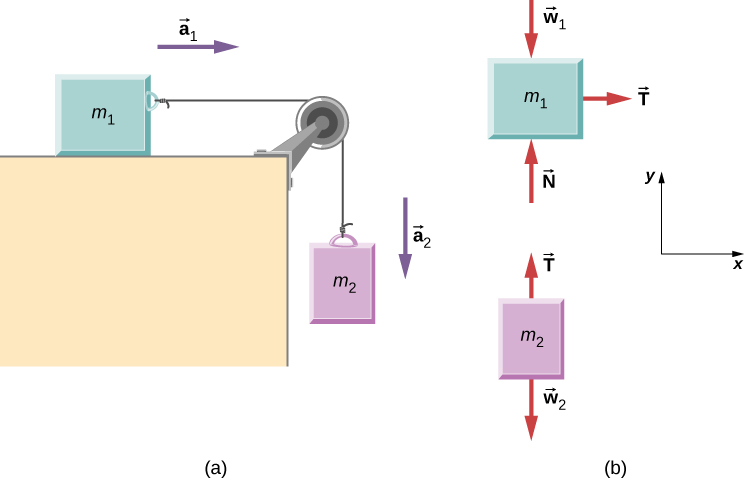
الشكل 6.6: (أ) يتم توصيل الكتلة m1 بواسطة خيط خفيف بالكتلة m2. (ب) مخططات الجسم الحر للكتل.
استراتيجية الحل
نرسم مخططًا للجسم الحر لكل كتلة على حدة، كما هو موضح في الشكل 6.6. ثم نقوم بتحليل كل واحد لإيجاد المجهول المطلوب. القوى الموجودة على الكتلة m1 هي قوة الجاذبية وقوة التلامس مع السطح وقوة شد الخيط. الكتلة m2 تخضع لقوة الجاذبية وقوة شد الخيط. ينطبق قانون نيوتن الثاني على كل منهما، لذلك نكتب معادلتين متجهتين كما يلي:
للكتلة الأولى:
T⃗ + w⃗ 1 + N⃗ = m1 a⃗1
وللكتلة الثانية:
T⃗ + w⃗ 2 = m 2 a⃗ 2
لاحظ أن T⃗ هو نفسه لكلا الكتلتين. نظرًا لأن الخيط والبكرة لهما كتلة ضئيلة، وبما أنه لا يوجد احتكاك في البكرة، فإن الشد هو نفسه في جميع أنحاء الخيط. يمكننا الآن كتابة معادلات المكونات لكل كتلة. جميع القوى إما أفقية أو رأسية، لذلك يمكننا استخدام نفس نظام الإحداثيات الأفقية / الرأسية لكلا الجسمين.
الحل
تتبع معادلات المكونات من معادلات المتجه أعلاه. نرى أن الكتلة 1 بها القوى الرأسية متوازنة، لذلك نتجاهلها ونكتب معادلة تتعلق بمكونات x. لا توجد قوى أفقية على الكتلة 2، لذلك تتم كتابة معادلة y فقط. نحصل على هذه النتائج:
الكتلة 1:
∑Fx = max
Tx = m1a1x
الكتلة 2:
∑Fy = may
Ty − m2g = m2a2y
عندما تتحرك الكتلة 1 إلى اليمين، فإن الكتلة 2 تتحرك مسافة مساوية لها إلى أسفل. وبالتالي، a1x = −a2y. كتابة التسارع المشترك للكتل على النحو التالي:
a = a1x = −a2y
لدينا الآن:
T = m1a
و
T − m2g = −m2a
من هاتين المعادلتين، يمكننا التعبير عن a و T بدلالة الكتل m1 وm2 و g:
a = (m2 / m1 + m2) g
و
T = (m1m2 / m1 + m2) g.
الدلالة
لاحظ أن الشد في الخيط أقل من وزن الكتلة المتدلية من نهايته. الخطأ الشائع في مثل هذه المسائل هو تحديد T = m2g. يمكنك أن ترى من مخطط الجسم الحر للكتلة 2 أن ذلك لا يمكن أن يكون صحيحًا إذا كانت الكتلة تتسارع.
تحقق من فهمك 6.2
احسب تسارع النظام والشد في الخيط عندما تكون الكتل m1 = 5.00 kg و m2 = 3.00 kg.
مثال 6.5: آلة أتوود
من تطبيقات قوانين نيوتن الشهيرة مسألة كلاسيكية في الفيزياء، مشابهة لتلك التي حللناها للتو، هي مسألة آلة أتوود، والتي تتكون من حبل يسير فوق بكرة، مع ربط جسمين من كتلة مختلفة. إنه مفيد بشكل خاص في فهم العلاقة بين القوة والحركة. في الشكل 6.7، m1 = 2.00 kg وm2 = 4.00 kg. اعتبر البكرة عديمة الاحتكاك. (أ) إذا تم تحرير m2، فماذا سيكون تسارعه؟ (ب) ما هو الشد في الخيط؟
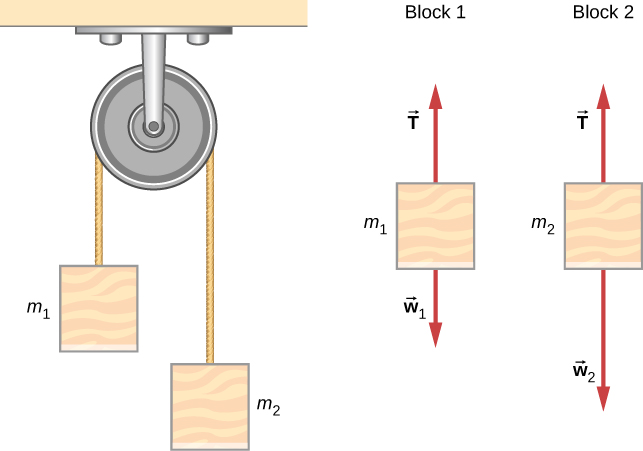
الشكل 6.7 آلة أتوود ومخططات الجسم الحر لكل من الكتلتين.
استراتيجية الحل
نرسم مخططًا للجسم الحر لكل كتلة على حدة، كما هو موضح في الشكل. ثم نقوم بتحليل كل رسم بياني لإيجاد المجهول المطلوب. قد يتضمن هذا حل المعادلات الآنية. من المهم أيضًا ملاحظة التشابه مع المثال السابق. عندما تتسارع الكتلة 2 مع تسارع مقداره a2 في الاتجاه الهابط، تتسارع الكتلة 1 باتجاه الأعلى مع التسارع a1. وبالتالي يكون، a = a1 = -a2.
الحل
(أ) لدينا:
Form1: ∑Fy = T − m1g = m1a
Form2: ∑Fy = T − m2g = m2a.
(تشير العلامة السالبة أمام m2a إلى أن m2 تتسارع إلى أسفل. كلتا الكتلتين تتسارع بنفس المعدل، ولكن في اتجاهين متعاكسين). قم بحل المعادلتين في وقت واحد (بطرحهما من بعضهما) والنتيجة هي:
(m2 − m1) g = (m1 + m2) . a
بحل المعادلة لإيجاد المجهول a:
a = (m2 − m1) / (m1+ m2) g = (4 kg – 2 kg) / (4kg + 2kg) (9.8m/s2) = 3.27 m/s2
(ب) بملاحظة الكتلة الأولى، نرى أن:
T − m1g = m1aT = m1 (g + a) = (2kg) (9.8 m/s2 + 3.27 m/s2) = 26.1N
الدلالة
يمكن تفسير نتيجة التسارع المعطى في الحل على أنه نسبة القوة غير المتوازنة على النظام، (m2-m1) g، إلى الكتلة الكلية للنظام، m1 + m2. يمكننا أيضًا استخدام آلة Atwood لقياس قوة مجال الجاذبية المحلية.
تحقق من فهمك 6.3
حدد معادلة عامة بدلالة m1 و m2 و g لحساب الشد في الخيط لجهاز Atwood الموضح أعلاه.
تطبيقات قوانين نيوتن للحركة وعلم الحركة
الفيزياء هي الأكثر إثارة للاهتمام والأقوى عند تطبيقها على المواقف العامة التي تنطوي على أكثر من مجموعة ضيقة من المبادئ الفيزيائية. يمكن أيضًا دمج تطبيقات قوانين نيوتن للحركة مع المفاهيم الأخرى التي تم مناقشتها سابقًا في هذا الكتاب لحل مسائل الحركة. على سبيل المثال، تنتج القوى تسارعًا، وهو موضوع علم الحركة، ومن ثم تظهر أهمية الفصول السابقة وعلاقتها به.
عند الاقتراب من المسائل التي تتضمن أنواعًا مختلفة من القوى، والتسارع، والسرعة، و/ أو الموضع، فإن سرد المعطيات والكميات التي سيتم حسابها سيسمح لك بتحديد المبادئ المعنية. بعد ذلك، يمكنك الرجوع إلى الفصول التي تتناول موضوعًا معينًا وحل المسألة باستخدام الاستراتيجيات الموضحة في الكتاب. يوضح المثال العملي التالي كيف يتم تطبيق استراتيجية حل المسائل الواردة سابقًا في هذا الفصل، بالإضافة إلى الاستراتيجيات المقدمة في فصول أخرى، على مسألة مفهوم متكامل.
مثال 6.6: ما القوة التي يجب أن يمارسها لاعب كرة القدم للوصول إلى السرعة القصوى؟
يبدأ لاعب كرة القدم من حالة السكون ويتسارع للأمام، حيث تصل سرعته إلى 8.00 م / ث في 2.50 ث. (أ) ما هو متوسط تسارعه؟ (ب) ما هو متوسط القوة التي تبذلها الأرض للأمام على العداء حتى يحقق هذه التسارع؟ علمًا بأن وزن اللاعب هو 70.0 كجم، ومقاومة الهواء ضئيلة.
استراتيجية الحل
للعثور على إجابات لهذه المسألة، نستخدم استراتيجية حل المسائل الواردة سابقًا في هذا الفصل. يوضح الحل الخاص بكل جزء من المثال كيفية تطبيق خطوات محددة لحل المسائل. في هذه الحالة، لا نحتاج إلى استخدام جميع الخطوات. نحن ببساطة نحدد المبادئ الفيزيائية، وبالتالي المعلومة والمجهولة؛ تطبيق قانون نيوتن الثاني؛ وتحقق لمعرفة ما إذا كانت الإجابة معقولة.
الحل
(أ) لدينا السرعات الأولية والنهائية (صفر و8.00 م / ث للأمام)؛ وبالتالي، فإن التغير في السرعة هو Δv = 8.00 m/s. لدينا الوقت المنقضي، لذا يكون Δt = 2.50 ثانية. المجهول هو التسارع الذي يمكن إيجاده من التعريف:
a = Δv / Δt
بالتعويض عن القيم المعروفة ينتج لنا:
a = [8.00 m/s] / 2.50 s = 3.20 m/s2
(ب) هنا يطلب منا إيجاد متوسط القوة التي تمارسها الأرض على العداء لإنتاج هذه التسارع. (تذكر أننا نتعامل مع القوة أو القوى التي تعمل على موضوع الاهتمام). هذه هي قوة رد الفعل لتلك التي يمارسها اللاعب للخلف على الأرض، بموجب قانون نيوتن الثالث. بإهمال مقاومة الهواء، سيكون هذا مساويًا في مقدار القوة الخارجية الصافية على اللاعب، لأن هذه القوة تسبب تسارعه. نظرًا لأننا نعرف الآن تسارع اللاعب ونحصل على كتلته، يمكننا استخدام قانون نيوتن الثاني لإيجاد القوة التي تمارس. وهذا كما يلي:
Fnet = m a
بالتعويض عن القيم المعروفة لـ m و a يعطينا:
Fnet = (70.0kg)(3.20m/s2) = 224 N
هذه نتيجة معقولة: يمكن تحقيق التسارع للرياضي في ظروف جيدة. القوة حوالي 50 رطلاً، وهو متوسط معقول للقوة.
الدلالة
يوضح هذا المثال كيفية تطبيق استراتيجيات حل المسائل على المواقف التي تتضمن موضوعات من فصول مختلفة. تتمثل الخطوة الأولى في تحديد المبادئ الفيزيائية والكميات المعروفة والمجهولة المتضمنة في المسألة. الخطوة الثانية هي الحل وإيجاد المجهول، في هذه الحالة باستخدام قانون نيوتن الثاني. أخيرًا، نتحقق من إجابتنا للتأكد من أنها معقولة. ستكون هذه التقنيات لمسائل المفاهيم المتكاملة مفيدة في تطبيقات الفيزياء خارج مقرر الفيزياء، كما هو الحال في مهنتك، في تخصصات العلوم الأخرى، وفي الحياة اليومية.
تحقق من فهمك 6.4
يتوقف لاعب كرة القدم بعد الانتهاء من اللعبة الموضحة أعلاه، لكنه يلاحظ الآن أن الكرة في وضع يسمح لها بالاستحواذ عليها. إذا واجه الآن قوة مقدارها 126 نيوتن لمحاولة الاستحواذ على الكرة، والتي تبعد عنه مسافة 2.00 متر، فكم من الوقت سيستغرقه للوصول إلى الكرة؟
مثال 6.7: ما القوة التي تعمل على نموذج طائرة هليكوبتر؟
تبلغ سرعة نموذج طائرة هليكوبتر تزن 1.50 كجم 5 jˆ m / s عند t = 0. يتم تسريعها بمعدل ثابت لمدة ثانيتين (2.00 ثانية) وبعد ذلك تكون السرعة (6 iˆ + 12.00 j^ m/s). ما مقدار القوة المحصلة المؤثرة على المروحية خلال هذه الفترة الزمنية؟
استراتيجية الحل
يمكننا بسهولة إعداد نظام إحداثيات يكون فيه المحور x (الاتجاه i) أفقيًا والمحور y (اتجاه jˆ) عموديًا. نعلم أن Δt = 2.00 s و Δv = (6.00 iˆ + 12.00 jˆm/s) – (5.00 jˆ m/s). من هذا يمكننا حساب التسارع من التعريف؛ يمكننا بعد ذلك تطبيق قانون نيوتن الثاني.
الحل
لدينا:
a = Δv/Δt = ((6.00 iˆ + 12.00 jˆ m/s) – (5.00 jˆ m/s)) / 2.00s = 3.00 iˆ + 3.50 j^ m/s2
∑F⃗ = m a⃗ = 1.5 kg (3.00 iˆ + 3.50 jˆ m/s2) = 4.50 iˆ + 5.25 jˆ N
يمكن الآن إيجاد مقدار القوة بسهولة:
F = √ ((4.50 N)2 + (5.25 N)2) = 6.91N
الدلالة
تم ذكر المسألة الأصلية بدلالة المكونات المتجهة iˆ, j^، لذلك استخدمنا طرق المتجهات. قارن هذا المثال بالمثال السابق.
تحقق من فهمك 6.5
أوجد اتجاه القوة المحصلة المؤثرة على نموذج طائرة الهليكوبتر التي تزن 1.50 كجم.
مثال 6.8: جرار الأمتعة
يوضح الشكل 6.8 (أ) جرار أمتعة يسحب عربات أمتعة من طائرة. كتلة الجرار 650.0 كجم، بينما العربة A كتلتها 250.0 كجم والعربة B كتلتها 150.0 كجم. تعمل القوة الدافعة التي تعمل لفترة وجيزة من الوقت على تسريع النظام من حالة السكون وتعمل لمدة 3.00 ثانية. (أ) إذا أعطيت هذه القوة الدافعة بواسطة F=820 t N ، أوجد السرعة بعد 3.00 ثوانٍ. (ب) ما هي القوة الأفقية المؤثرة على الكيبل الواصل بين الجرار والعربة أ في هذه اللحظة؟
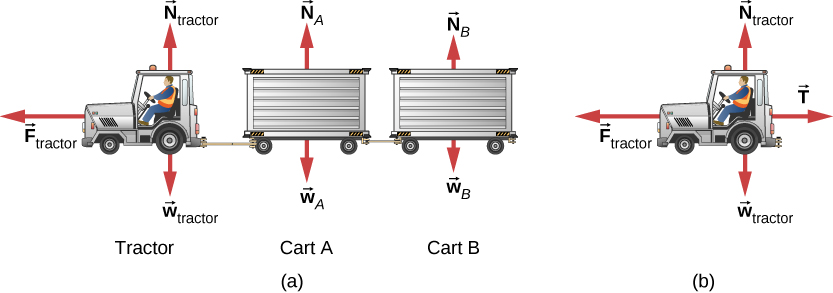
الشكل 6.8 (أ) يظهر رسم تخطيطي للجسم الحر، والذي يشير إلى جميع القوى الخارجية المؤثرة على النظام، والتي تتكون من الجرار وعربات الأمتعة لنقل أمتعة شركات الطيران. (ب) يتم عرض مخطط الجسم الحر للجرار فقط معزولًا من أجل حساب التوتر في الكيبل للعربات.
استراتيجية الحل
يوضح مخطط الجسم الحر القوة الدافعة للجرار، مما يعطي النظام تسارعه. نحتاج فقط إلى النظر في الحركة في الاتجاه الأفقي. توازن القوى الرأسية يلغي بعضها البعض وليس من الضروري أخذها في الاعتبار. بالنسبة للجزء ب، فإننا نستخدم مخطط الجسم الحر للجرار وحده لتحديد القوة بينه وبين العربة A. وهذا يكشف قوة الربط بينهما T⃗، وهو هدفنا.
الحل
(أ) لدينا
∑Fx = ∑msystem ax
Fx = 820.0t
820 t a = (650.0 + 250.0 + 150.0)
a = 0.7809 t
نظرًا لأن التسارع دالة في الزمن، يمكننا تحديد سرعة الجرار باستخدام التفاضل a = dv/dt مع الشرط الأولي الذي ينطبق غي حالة البدء من السكون v0 = 0 عند t = 0. نقوم بإجراء التكامل من t = 0 إلى t = 3:
dv = a dt
∫(0,3) dv = ∫(0,3) a dt = ∫(0,3)(0.7809 t) dt
v = (0.3905 t2)/ 2 = 3.51 m/s
(ب) بالرجوع إلى مخطط الجسم الحر في الشكل 6.8 (ب).
∑Fx = m tractor a x 820.0t – T = m tractor (0.7805)t (820.0)(3.0) – T
= (650.0) (0.7805) (3.00) T = 938 N
الدلالة
نظرًا لأن القوة تختلف مع الوقت، يجب علينا استخدام حساب التفاضل والتكامل لحل هذه المسألة. لاحظ كيف أن الكتلة الإجمالية للنظام كانت مهمة في حل الشكل 6.8 (أ)، بينما كانت كتلة الشاحنة فقط (منذ أن زودت بالقوة) هي المستخدمة في الشكل 6.8 (ب).
تطبيقات قوانين نيوتن واستخدام التفاضل والتكامل
في كثير من الأحيان عند حل مسائل تطبيقات قوانين نيوتن تذكر أن v = ds/dt و a = dv/dt. إذا كان التسارع دالة زمنية، فيمكننا استخدام صيغ حساب التفاضل والتكامل المطورة في الحركة على طول الخط المستقيم، كما هو موضح في هذا المثال. ومع ذلك، فإن التسارع في بعض الأحيان يكون دالة على الإزاحة. في هذه الحالة، يمكننا استنباط نتيجة مهمة من علاقات التفاضل والتكامل هذه. لحل dt في كل منهما، لدينا dt = ds v و dt = dv a. الآن، بمساواة هذه التعبيرات، يكون لدينا ds v = dv a. يمكننا إعادة ترتيب هذا للحصول على ads = v dv.
مثال 6.9: حركة مقذوف تم إطلاقه عموديًا
تُطلق قذيفة هاون تزن 10.0 كجم عموديًا من الأرض بسرعة ابتدائية 50.0 م / ث (انظر الشكل 6.9). حدد الحد الأقصى للارتفاع الذي ستنتقله القذيفة إذا تم قياس مقاومة الغلاف الجوي على أنها FD = (0.0100 v2) N، حيث v هي السرعة في أي لحظة.

الشكل 6.9 (أ) تطلق قذيفة الهاون قذيفة بشكل مستقيم لأعلى؛ تؤخذ بالاعتبار قوة الاحتكاك التي يوفرها الهواء. (ب) يظهر رسم تخطيطي للجسم الحر يوضح جميع القوى المؤثرة على قذيفة الهاون. (المصدر: المعلومات المرئية لوزارة الدفاع الأمريكية).
استراتيجية الحل
يمكن أن تكون القوة المعروفة المؤثرة على قذيفة الهاون مرتبطة بتسارعها باستخدام معادلات الحركة. يمكن بعد ذلك استخدام علم الحركة لربط تسارع قذيفة الهاون بموقعها.
الحل
في البداية، y0 = 0 و v0 = 50.0 m/s. عند أقصى ارتفاع y=h، v=0. يُظهر مخطط الجسم الحر أن FD يعمل باتجاه الأسفل، لأنه يبطئ الحركة الصعودية لقذيفة الهاون. وهكذا يمكننا أن نكتب
∑ Fy = m a y
– FD – w = may – 0.0100 v2 − 98.0 = 10.0 a
a = − 0.00100 v2 − 9.80
يعتمد التسارع على v وبالتالي فهو متغير. نظرًا لأن a = f(v)، يمكننا ربط a بـ v باستخدام إعادة الترتيب الموصوف أعلاه،
ads = vdv
نستبدل ds بـ dy لأننا نتعامل مع الاتجاه العمودي،
ady = vdv
(−0.00100 v2 – 9.80) dy = vdv
نحن الآن نفصل بين المتغيرات (v’s و dv’s على جانب واحد؛ dy على الجانب الآخر):
∫0hdy = ∫050.0vdv (−0.00100 v2 – 9.80) ∫0hdy = −∫050.0vdv (0.00100v2 + 9.80) = (- 5 × 102) ln (0.00100 v2 + 9.80) ∣ 050.0
وهكذا، ينتج لنا الارتفاع:
h = 114 m
الدلالة
لاحظ الحاجة إلى تطبيق التفاضل والتكامل لأن القوة ليست ثابتة، مما يعني أيضًا أن التسارع ليس ثابتًا. لجعل الأمور أسوأ، تعتمد القوة على v (وليس t)، ولذا يجب علينا استخدام الحيلة الموضحة قبل المثال. تشير إجابة الارتفاع إلى ارتفاع منخفض إذا كانت هناك مقاومة للهواء. سنتعامل مع تأثيرات مقاومة الهواء وقوى السحب الأخرى بمزيد من التفصيل في قوة السحب وقوة المحطة Terminal Speed.
تحقق من فهمك 6.6
إذا تم إهمال مقاومة الغلاف الجوي، ابحث عن أقصى ارتفاع لقذيفة الهاون. هل حساب التفاضل والتكامل مطلوب لهذا الحل؟
تعليم تفاعلي
استكشف القوى المؤثرة في هذه المحاكاة عندما تحاول دفع خزانة الملفات. قم بإنشاء قوة مطبقة وشاهد قوة الاحتكاك الناتجة والقوة الكلية التي تعمل على الخزانة. توضح الرسوم البيانية القوى والموضع والسرعة والتسارع مقابل الوقت. اعرض مخطط الجسم الحر لجميع القوى (بما في ذلك قوى الجاذبية والقوى العادية).
المراجع
- موسوعة الفيزياء العامة، ترجمة وإعداد: د. م. مصطفى عبيد، مركز البحوث والدراسات متعدد التخصصات، إسطنبول، 2022.
- كتاب الفيزياء للجامعات، صموئيل جيه لينغ، جامعة ولاية ترومان، د. جيف ساني، جامعة لويولا ماريماونت ويليام مويبس.





