المعالجة الرياضية لنتائج القياس
بنهاية هذا القسم المخصص لشرح وتبسيط موضوع تحويل الوحدات المخصصة للقياس والمعالجة الرياضية لنتائج القياس، ستكون قادرًا على:
- شرح نهج تحليل الأبعاد (تسمية العوامل) للحسابات الرياضية التي تنطوي على الكميات (معالجة الأعداد وتحويل وحدات قياس).
- استخدام التحليل البُعدي لإجراء تحويلات الوحدة لخاصية معينة وعمليات حسابية تتضمن خاصيتين أو أكثر.
- فهم طرق ومعادلات تحويل وحدات قياس درجات الحرارة الأكثر استخدامًا في الكيمياء
المحتويات
غالبًا ما يكون الأمر هو أن الكمية محل البحث قد لا يكون من السهل (أو حتى من الممكن) قياسها بشكل مباشر ولكن بدلاً من ذلك يجب حسابها من الخصائص الأخرى المقاسة مباشرة والعلاقات الرياضية المناسبة. على سبيل المثال، ضع في اعتبارك قياس متوسط سرعة العدو في سباقات السرعة. يتم تحقيق ذلك عادةً عن طريق قياس الزمن المطلوب للرياضي للركض من خط البداية إلى خط النهاية، والمسافة بين هذين الخطين، ثم حساب السرعة من المعادلة التي تتعلق بهذه الخصائص الثلاثة:
السرعة = المسافة / الزمن
يمكن لعدّاء بجودة أولمبية الركض لمسافة 100 متر في حوالي 10 ثوانٍ، وهو ما يقابل متوسط سرعة = 100 متر / 10 ثانية = 10 م / ث.
تحويل وحدات القياس
لاحظ أن هذا الحساب البسيط يتضمن قسمة أعداد كل كمية مقاسة لإعطاء عدد الكمية المحسوبة (100/10 = 10) وكذلك قسمة وحدات قياس كل كمية مقاسة لإعطاء وحدة قياس الكمية المحسوبة (متر / ثانية = متر / ثانية).
الآن، نفرض أننا نريد استخدام هذه العلاقة نفسها للتنبؤ بالوقت المطلوب لشخص يركض بهذه السرعة ليقطع مسافة 25 مترًا. يتم استخدام نفس العلاقة بين الخصائص الثلاث، ولكن في هذه الحالة، الكميتان المقدمتان هما السرعة (10 م / ث) والمسافة (25 م). للحصول على الخاصية المطلوبة، الزمن، يجب إعادة ترتيب المعادلة بشكل مناسب:
الزمن = المسافة / السرعة
يمكن بعد ذلك حساب الزمن على النحو التالي:
25 متر / 10 متر / ثانية = 2.5 ثانية
مرة أخرى، كان الحساب على الأعداد (25/10 = 2.5) مصحوبًا بنفس الحساب على وحدات القياس (متر / (متر / ثانية) = ثانية)، لإعطاء عدد ووحدة قياس للنتيجة، 2.5 ثانية. لاحظ أنه، كما هو الحال بالنسبة للأعداد، عندما تقسم وحدة قياس على وحدة قياس متطابقة (في هذه الحالة، قسمة متر / متر)، تكون النتيجة “1”، أو، كما هو شائع، “تُلغي” الوحدات بعضها البعض.
هذه الحسابات هي أمثلة على نهج رياضي متعدد الاستخدامات يُعرف باسم التحليل البُعدي أو تحليل الأبعاد (أو طريقة عامل التسمية). يعتمد تحليل الأبعاد على هذه الفرضية: يجب أن تخضع وحدات قياس الكميات لنفس العمليات الحسابية مثل الأعداد المرتبطة بها. يمكن تطبيق هذه الطريقة على حسابات تتراوح من تحويلات بسيطة للوحدات إلى حسابات أكثر تعقيدًا ومتعددة الخطوات تتضمن كميات مختلفة.
عوامل تحويل الوحدات وتحليل الأبعاد
يمكن استخدام النسبة بين كميتين متكافئتين معبرًا عنها بوحدات قياس مختلفة كعامل تحويل للوحدة. على سبيل المثال، أطوال 2.54 سم و1 بوصة متكافئة (حسب التعريف)، وبالتالي يمكن اشتقاق عامل تحويل الوحدة من النسبة كما يلي:
بما أنه لدينا:
1 بوصة = 2.54 سم
بالضرب في س (أي عدد مهما كان)، ينتج لنا:
س × بوصة = س × 2.54 سم / 1 بوصة، حيث (2.54 سم = 1 بوصة)
أو:
س بوصة = س × 2.54 سم / بوصة.
عوامل تحويل الوحدات الشائعة
يتم إعطاء العديد من عوامل تحويل الوحدات الأخرى شائعة الاستخدام في الجدول 1.6.
| الكتلة | الحجم | الطول |
| 1 kg = 2.2046 lb | L = 1.0567 qt | 1 m = 1.0936 yd |
| 1 lb = 453.59 g | 1 qt = 0.94635 L | 1 in. = 2.54 cm (exact) |
| 1 (avoirdupois) oz = 28.349 g | 1 ft3 = 28.317 L | 1 km = 0.62137 mi |
| 1 (troy) oz = 31.103 g | 1 tbsp = 14.787 mL | 1 mi = 1609.3 m |
عندما نضرب كمية (مثل المسافة المحددة بالبوصة) في عامل تحويل وحدة مناسب، نقوم بتحويل الكمية إلى قيمة مكافئة بوحدات مختلفة (مثل المسافة بالسنتيمتر). على سبيل المثال، يمكن تحويل القفزة العمودية للاعب كرة السلة البالغة 34 بوصة إلى سنتيمترات عن طريق ما يلي:
34 بوصة × 2.54 سم / 1 بوصة = 86 سم
نظرًا لأن هذا الحساب البسيط يتضمن كميات، فإن فرضية تحليل الأبعاد تتطلب أن نضرب كلًا من الأعداد والوحدات. يتم ضرب أعدد هاتين الكميتين للحصول على عدد كمية الناتج، 86، في حين يتم ضرب الوحدات للحصول على (بوصة × سم / بوصة). كما هو الحال بالنسبة للأعداد، فإن النسبة بين الوحدات المتطابقة تساوي عدديًا واحدًا، (بوصة / بوصة = 1)، وبالتالي يتم تبسيط حاصل ضرب الوحدات إلى سم. (عندما تقسم الوحدات المتطابقة لإعطاء العامل 1، يُقال إنها “تلغي بعضها”).
باستخدام تحليل الأبعاد، يمكننا تحديد أن عامل تحويل الوحدة قد تم إعداده بشكل صحيح عن طريق التحقق للتأكد من إلغاء الوحدة الأصلية، وستحتوي النتيجة على الوحدة المطلوبة (المحولة).
مثال 1.8: استخدام معامل تحويل الوحدات
تبلغ كتلة الطير المنافس 125 جم. قم بتحويل كتلته إلى أوقية باستخدام عامل تحويل الوحدة المشتق من العلاقة 1 أوقية = 28.349 جم (الجدول 1.6).
الحل
إذا كان لدينا عامل التحويل، فيمكننا تحديد الكتلة بالكيلوجرام باستخدام معادلة تشبه تلك المستخدمة لتحويل الطول من البوصة إلى السنتيمترات.
س x أوقية = 125 جم × معامل تحويل الوحدة
نكتب عامل تحويل الوحدة في شكليه:
1 أوقية / 28.35 جرام
28.349 جرام / 1 أوقية
عامل تحويل الوحدة الصحيح هو النسبة التي تلغي وحدات الجرامات والأوقية.
س x أوقية = 125 جم × (1 أوقية / 28.349 جرام) = (125 / 28.349) أوقية
= 4.41 أوقية (مقرب إلى ثلاثة أرقام مهمة)
تحقق من فهمك:
حول حجم 9.345 كوارت (ربع جالون بالنظام الأمريكي qt) إلى لتر.
تحويل الوحدات في مسائل حسابية
بالإضافة إلى تحويلات الوحدات البسيطة، يمكن استخدام طريقة تسمية العوامل لحل المسائل الأكثر تعقيدًا التي تنطوي على عمليات حسابية. بغض النظر عن التفاصيل، فإن النهج الأساسي هو نفسه – يجب أن تكون جميع العوامل المتضمنة في الحساب موجهة بشكل مناسب للتأكد من أن تسمياتها (الوحدات) ستلغي و/ أو تتحد بشكل مناسب لإنتاج الوحدة المطلوبة في النتيجة. هذا هو السبب في أنه يشار إليها باسم طريقة تسمية العوامل. مع استمرار دراستك للكيمياء، ستواجه العديد من الفرص لتطبيق هذا النهج.
مثال 1.9: حساب الكميات من نتائج القياس والعلاقات الرياضية المعروفة
ما هي كثافة مضاد التجمد الشائع بوحدات جم / مل؟ إذا كانت عينة بحجم 4.00-qt من مانع التجمد تزن 9.26 رطل.
الحل
بما أن الكثافة = الكتلة / الحجم، علينا قسمة الكتلة بالجرام على الحجم بالملليلترات. بشكل عام: عدد وحدات B = عدد الوحدات A × معامل تحويل الوحدة. ترد عوامل التحويل الضرورية في الجدول 1.6:
1 رطل = 453.59 جم؛ 1 لتر = 1.0567 كوارت؛ 1 لتر = 1000 مل، يمكننا تحويل الكتلة من أرطال إلى جرامات في خطوة واحدة:
9.26 رطل × 453.59 جم / 1 رطل = 4.20 × 10 3 جرام
نحتاج إلى استخدام خطوتين لتحويل الحجم من لتر إلى مليلتر:
الخطوة 1: التحويل من كوارت إلى لتر.
4.00 كوارت × 1 لتر / 1.0567 كوارت = 3.78 لتر
الخطوة 2: تحويل اللترات إلى ملليلتر.
3.78 لتر × 1000 مل / 1 لتر = 3.78 × 10 3 مل
ثم،
الكثافة = 4.20 × 10 3 جم / 3.78 × 10 3 مل = = 1.11 جم / مل
بدلاً من ذلك، يمكن إعداد الحساب بطريقة تستخدم ثلاث معاملات تحويل للوحدات بالتتابع مثل:
(9.26 رطل / 4.00 كوارت) × (453.59 جرام / 1 رطل) × (1.0567 كوارت / 1 لتر) × (1 لتر / 1000 مل) = 1.11 جم / مل
تحقق من فهمك
ما هو الحجم باللتر لـ 1.000 أوقية، مع العلم أن 1 لتر = 1.0567 كوارت و1 كوارت = 32 أوقية (بالضبط)؟
الجواب: 2.956 × 10−2 لتر.
مثال 1.10: حساب الكميات من نتائج القياس والعلاقات الرياضية المعروفة
أثناء القيادة من فيلادلفيا إلى أتلانتا، على مسافة حوالي 1250 كيلومترًا، تستخدم سيارة لامبورغيني أفينتادور رودستر موديل 2014 ما مقداره 213 لترًا من البنزين.
- (أ) ما هو متوسط استهلاك الوقود، بالأميال للغالون الواحد، الذي قامت به سيارة رودستر خلال هذه الرحلة؟
- (ب) إذا كان سعر البنزين 3.80 دولارًا أمريكيًا للغالون الواحد، فما هي تكلفة الوقود لهذه الرحلة؟
الحل
(أ) نقوم أولاً بتحويل المسافة من كيلومترات إلى أميال:
1250 كم × 0.62137 ميل / 1 كم = 777 ميل
ثم نقوم بتحويل الحجم من اللترات إلى الجالونات:
213 لتر × (1.0567 كوارت / 1 لتر) × (1 جالون / 4 كوارت) = 56.3 جالون
ثم،
(متوسط) الأميال = 777 ميل / 56.3 جالون = 13.8 ميل / جالون = 13.8 ميلا لكل غالون.
بدلاً من ذلك، يمكن إعداد الحساب بطريقة تستخدم جميع عوامل التحويل بالتتابع، على النحو التالي:
(1250 كم / 213 لتر) × (0.62137 ميل / 1 كم) × (1 لتر / 1.0567 كوارت) × (4 كوارت / 1 جالون) = 13.8 ميل / الغالون
(ب) باستخدام الحجم المحسوب مسبقًا بالجالونات، نجد:
56.3 جالون × 3.80 دولار / 1 جالون = 214 دولارًا.
تحقق من فهمك
تستخدم سيارة تويوتا بريوس هايبرد 59.7 لترًا من البنزين للقيادة من سان فرانسيسكو إلى سياتل، على مسافة 1300 كم (رقمان مهمان أو ذات معنى أو دلالة).
- (أ) ما هو متوسط استهلاك الوقود، بالأميال للغالون الواحد، الذي استهلكته سيارة بريوس خلال هذه الرحلة؟
- (ب) إذا كان سعر البنزين 3.90 دولارًا للغالون الواحد، فما هي تكلفة الوقود لهذه الرحلة؟
الجواب: (أ) 51 ميلا لكل الغالون؛ (ب) 62 دولارًا.
تحويل وحدات قياس درجة الحرارة
نستخدم كلمة درجة الحرارة للإشارة إلى سخونة أو برودة مادة ما. إحدى الطرق التي نقيس بها التغير في درجة الحرارة هي استخدام حقيقة أن معظم المواد تتمدد عندما ترتفع درجة حرارتها وتنكمش عندما تنخفض درجة حرارتها. يغير الزئبق أو الكحول في ميزان حرارة زجاجي شائع حجمه مع تغير درجة الحرارة. نظرًا لأن حجم السائل يتغير أكثر من حجم الزجاج، يمكننا أن نرى السائل يتمدد عندما يصبح أكثر دفئًا وينكمش عندما يصبح أكثر برودة.
التحويل بين الدرجة المئوية والفرهنهايت
لتمييز مقياس على ميزان حرارة، نحتاج إلى مجموعة من القيم المرجعية: اثنتان من أكثرها شيوعًا هي درجات حرارة غليان وتجميد الماء عند ضغط جوي محدد. على مقياس سيليزيوس، يتم تعريف صفر درجة مئوية على أنها درجة حرارة تجمد الماء و100 درجة مئوية على أنها درجة حرارة غليان الماء. المسافة بين درجتي الحرارة مقسمة إلى 100 فترة متساوية، والتي نسميها بالدرجات. على مقياس فهرنهايت، يتم تحديد نقطة تجمد الماء على أنها 32 درجة فهرنهايت ودرجة حرارة الغليان هي 212 درجة فهرنهايت. المسافة بين هاتين النقطتين على مقياس حرارة فهرنهايت مقسمة إلى 180 جزءًا متساويًا (درجات).
يؤدي تحديد مقاييس درجة الحرارة المئوية والفهرنهايت كما هو موضح في الفقرة السابقة إلى علاقة أكثر تعقيدًا بعض الشيء بين قيم درجة الحرارة على هذين المقياسين مقارنة بوحدات القياس المختلفة للخصائص الأخرى. معظم وحدات القياس لخاصية معينة تتناسب طرديًا مع بعضها البعض (ص = ث × س). استخدام وحدات الطول المألوفة كأحد الأمثلة:
الطول بالقدم = 1 قدم / 12 بوصة × الطول بالبوصة
حيث ص = الطول بالأقدام، س = الطول بالبوصة، وثابت التناسب ث، هو عامل التحويل. ومع ذلك، لا تشترك مقاييس درجة الحرارة المئوية والفهرنهايت في نقطة الصفر المشتركة، وبالتالي فإن العلاقة بين هذين المقياسين هي علاقة خطية وليست تناسبية (ص = م س + ب). وبالتالي، فإن تحويل درجة حرارة من أحد هذين المقياسين إلى الآخر يتطلب أكثر من مجرد عملية ضرب بواسطة عامل تحويل، m، كما يجب أن يؤخذ في الاعتبار الاختلافات في نقاط الصفر للمقياس (ب).
اشتقاق معادلة التحويل
تُشتق المعادلة الخطية المتعلقة بدرجات الحرارة المئوية والفهرنهايت بسهولة من درجتي الحرارة المستخدمتين لتحديد كل مقياس. تمثيل درجة الحرارة المئوية كـ x ودرجة حرارة فهرنهايت كـ y، المنحدر، m، يتم حسابه ليكون:
ثم يتم حساب تقاطع ص للمعادلة، ب، باستخدام أي من أزواج درجة الحرارة المكافئة، (100 درجة مئوية، 212 درجة فهرنهايت) أو (0 درجة مئوية، 32 درجة فهرنهايت)، على النحو التالي:
ب = ص – م س
ب = 32 درجة فهرنهايت – (9 درجة فهرنهايت / 5 درجة مئوية) × (0 درجة مئوية) = 32 درجة فهرنهايت
ومن ثم فإن المعادلة المتعلقة بمقاييس درجة الحرارة هي:
درجة الحرارة بالفهرنهايت ف = (9 درجة فهرنهايت / 5 درجة مئوية × درجة مئوية) + 32 درجة مئوية
أو بالرموز:
الشكل المختصر لهذه المعادلة بعد حذف وحدات القياس هو:
ينتج عن إعادة ترتيب هذه المعادلة الشكل المفيد للتحويل من درجات فهرنهايت إلى درجات مئوية:
التحويل من وإلى وحدات الكلفن
كما ذكرنا سابقًا في هذا الفصل، فإن وحدة درجة الحرارة في النظام الدولي للوحدات هي كلفن (K). على عكس مقياسي Celsius وFahrenheit، فإن مقياس كلفن هو مقياس درجة حرارة مطلقة حيث يتوافق الصفر بمقياس K مع أدنى درجة حرارة يمكن تحقيقها نظريًا. اقترح اكتشاف العلاقة بين حجم الغاز ودرجة الحرارة في أوائل القرن التاسع عشر أن حجم الغاز سيكون صفرًا عند -273.15 درجة مئوية. في عام 1848، اقترح الفيزيائي البريطاني ويليام طومسون، الذي تبنى لاحقًا لقب اللورد كلفن، مقياسًا مطلقًا لدرجة الحرارة بناءً على هذا المفهوم (تم توفير مزيد من المعالجة لهذا الموضوع في فصل خاص ضمن هذا الكتاب عن الغازات).
درجة حرارة التجمد للماء على هذا المقياس هي 273.15 كلفن ودرجة حرارة الغليان 373.15 كلفن، لاحظ أن الفرق العددي في هاتين الدرجتين المرجعيتين هو 100، وهو نفس الاختلاف في المقياس المئوي، وبالتالي فإن العلاقة الخطية بين هذين المقياسين لدرجات الحرارة ستظهر خط مائل 1-K/C. باتباع نفس النهج، يتم اشتقاق معادلات التحويل بين مقياسي درجة الحرارة كلفن ودرجة الحرارة المئوية لتكون كما يلي:
تم تحديد 273.15 في هذه المعادلات تجريبيًا، لذا فهي ليست دقيقة. يوضح الشكل 1.28 العلاقة بين مقاييس درجة الحرارة الثلاثة. تذكر أننا لا نستخدم علامة الدرجة مع درجات الحرارة بمقياس كلفن.
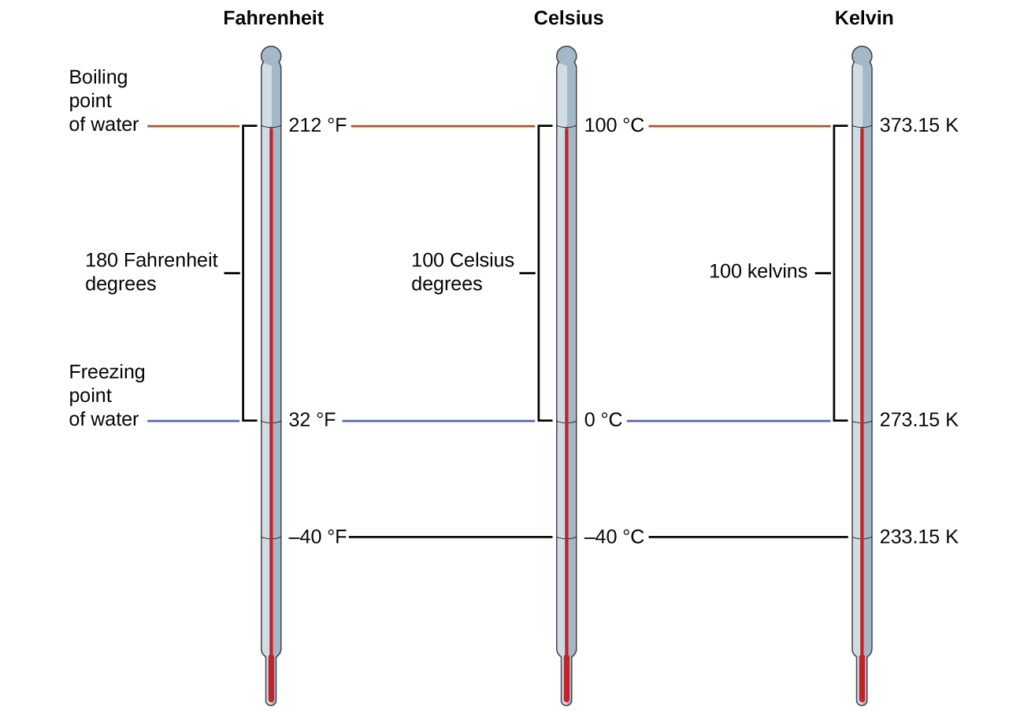
على الرغم من أن مقياس درجة الحرارة كلفن (المطلق) هو مقياس درجة الحرارة الرسمي في نظام الوحدات الدولي SI، إلا أن الدرجة المئوية تستخدم بشكل شائع في العديد من السياقات العلمية وهي المقياس المفضل للسياقات غير العلمية في جميع مناطق العالم تقريبًا. لا يزال عدد قليل جدًا من البلدان (الولايات المتحدة وأقاليمها، وجزر الباهاما، وبليز، وجزر كايمان، وبالاو) يستخدم فهرنهايت في مجالات الطقس والطب والطهي.
مثال 1.11: التحويل من الدرجة المئوية
تم قبول درجة حرارة الجسم الطبيعية بشكل عام على أنها 37.0 درجة مئوية (على الرغم من أنها تختلف حسب الوقت من اليوم وطريقة القياس، وكذلك بين الأفراد). ما درجة الحرارة هذه على مقياس كلفن وعلى مقياس فهرنهايت؟
الحل:
درجة الحرارة بالكلفن ك = الدرجة المئوية + 273.15 = 37.0 + 273.2 = 310.2 كلفن.
درجة الحرارة بالفهرنهايت = (9/5 × 37) + 32 = 66.6 + 32.0 = 98.6 درجة فهرنهايت.
تحقق من فهمك:
تحويل 80.92 درجة مئوية إلى كلفن ودرجة فهرنهايت.
الإجابة: 354.07 كلفن، 177.7 درجة فهرنهايت.
مثال 1.12: التحويل من فهرنهايت
يتطلب خبز البيتزا الجاهزة درجة حرارة فرن تبلغ 450 درجة فهرنهايت. إذا كنت في أوروبا، وكان ميزان حرارة الفرن الخاص بك يستخدم مقياس درجة مئوية، فما هو الإعداد الصحيح للفرن؟ ما هي درجة حرارة كلفن؟
الحل:
درجة الحرارة بالدرجات المئوية = (5/9) × (الدرجة بالفهرنهايت – 32) = 5/9 × (450 – 32) = 232 درجة مئوية. “اضبط الفرن على 230 درجة مئوية”. (التقريب إلى رقمين مهمين).
درجة الحرارة بالكلفن = درجة الحرارة المئوية + 273.15 = 230 + 273 = 503 كلفن = 5.0 × 10 2 كلفن (رقمين مهمين).
تحقق من فهمك:
تحويل 50 درجة فهرنهايت إلى درجة مئوية وكلفن.
الجواب: 10 درجات مئوية، 280 كلفن.
المراجع
- مقرر الكيمياء، كلية OpenStax، سنة OpenStax College, Chemistry ،2015. الفصل الأول: الأفكار والمفاهيم الاساسية في الكيمياء.
- موسوعة الكيمياء من الألف إلى الياء، ترجمة وإعداد: د. م. مصطفى عبيد، مركز البحوث والدراسات متعدد التخصصات، إسطنبول، 2022-2023.