حفظ الزخم Conservation of Momentum
توصلنا إلى أن الدفع الذي يتلقاه الجسم بفعل قوة تؤثر عليه خلال فترة معينة يساوي التغير في زخم الجسم خلال نفس الفترة.
فإذا كانت محصلة القوى الخارجية المؤثرة على مجموعة من الأجسام تساوي صفرًا سُميت مجموعة الأجسام بالنظام المعزول.
والقوى الوحيدة التي تؤثر في النظام المعزول هي القوى المتبادلة بين الأجسام أو الجسيمات داخل هذا النظام.
أي أنه في النظام المعزول ميكانيكيًا يكون:
F ∆t = ∆P = Pfinal – Pinitial = 0
حيث أن Pfinal و Pinitial ترمزان لزخم النظام الابتدائي (قبل) والنهائي (بعد) التغير. كما أن:
P final = P initial = مقدار ثابت
وعند ثبوت أي كمية فيزيائية خلال أي عملية فإنه يُقال أن هذه الكمية محفوظة.
قانون حفظ الزخم
إذا كانت محصلة القوى الخارجية المؤثرة على مجموعة من الأجسام بينها تأثير متبادل في نظام مغلق (مجموعة الأجسام التي تبقى كتبتها ثابتة خلال أية عملية تبادل للقوى) تساوي صفرًا، فإن مجموع زخم هذه الأجسام يبقى ثابتًا أو محفوظًا.
∑ P final = ∑ P initial
في الشكل التالي:
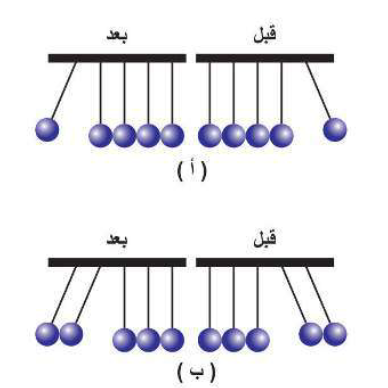
عند اصطدام كرة واحدة من الطرف الأيمن بمجموعة من الكرات الساكنة يؤدي ذلك إلى اندفاع كرة واحدة من الطرف الأيسر وارتفاعها تقريبًا يساوي ارتفاع الكرة الأولى. أما عند اصطدام كرتين من الطرف الأيمن فإن ذلك يؤدي إلى اندفاع كرتين من الطرف الأيسر بنفس الطريقة تقريبًا. وهذا يعني أن الزخم للمجموعة قبل التصادم يساوي الزخم بعد التصادم.
مثال (4)
يجلس ولد كتلته (35 kg) في قارب ساكن كتلته (65 kg) ويحمل صندوقًا كتلته (6 kg). فإذا قذف الولد الصندوق أفقيًا بسرعة مقدارها (10 m/s)، ومع إهمال مقاومة الماء، جد سرعة القارب بعد قذف الصندوق مباشرة.
الحل
نفرض أن:
كتلة الولد m1
كتلة القارب m2
سرعة القارب الابتدائية = vi = صفر (حالة السكون)
سرعة الصندوق النهائية = v1f
سرعة القارب النهائية = v2f
حيث أن:
∑ P final = ∑ P initial
بالتعويض عن قيمة الزخم للطرفين، الابتدائية والنهائية، أي أن:
(m1 + m2) . vi = m1 v1f + m2 v2f
0 = 6 × 10 + 100 (v2f(
v2f = – 0.60 m/s
والإشارة السالبة تعني أن القارب سوف يندفع بالاتجاه المعاكس لاتجاه قذف الكرة.





