القانون الثاني لنيوتن في الحركة الدورانية
تطبيق القانون الثاني لنيوتن في الحركة الدورانية
في الشكل التالي جسم كتلته m يتحرك حركة دورانية في مسار دائري نصف قطره r تحت تأثير قوة مماسية مقدارها Ft وتتولد نتيجة لذلك قوة مركزية FC باتجاه المركز.
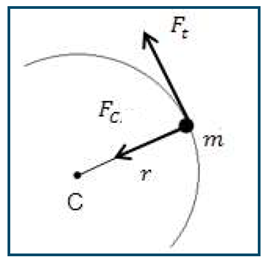
بتطبيق قانون نيوتن الثاني:
Ft = m at
حيث at هو التسارع الخطي المماسي، والذي يساوي:
at =
ويكون العزم الدوراني Ꚍ يساوي:
Ꚍ = Ft × r
بالتعويض عن كل من Ft وat ينتج أن:
Ꚍ = Ft × r = [m at] × r = [m × α × r] × r = m α r2
أي أن:
Ꚍ = m α r2
أو:
Ꚍ = (m r2) × α
ولكن من معادلة حساب القصور الدوراني، لدينا:
I = m r2
بالتعويض ينتج أن:
Ꚍ = I × α
وهذه المعادلة هي نتيجة مترتبة على قانون نيوتن الثاني والتي تنص على أنه: يتناسب التسارع الزاوي لجسم يتحرك دورانيًا حول محور طرديًا مع محصلة العزوم المؤثرة فيه وعكسيًا مع قصوره الدوراني بالنسبة للمحور نفسه. أي أن:
α = Ꚍ / I
التفسير الفيزيائي
لتوضيح مفهوم النتيجة التي تم التوصل إليها حول علاقة التسارع الزاوي بالقصور الدوراني ومحصلة العزوم المؤثرة على جسم، يمكن تصور الفرق بين حركة الجسمين المبينين بالشكل التالي:
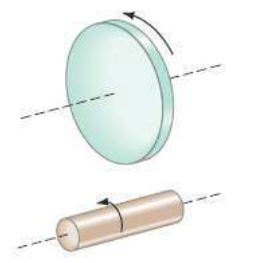
فبالرغم من أن الجسمين متساويان في الكتلة، إلا أن تأثير العزم على الأول أكبر من تأثيره على الثاني، وذلك نظرًا لأنه يدور حول محور بنصف قطر أكبر من الثاني، وبالتالي فإن القصور الدوراني له يكون أقل من الثاني. وهذا هو الاختلاف بين الحركة المستقيمة التي تعتمد على الكتلة فقط وبين الحركة الدورانية التي تعتمد على عوامل أخرى مثل نصف قطر الدائرة r.
مثال (3)
يتحرك جسم نقطي كتلته (2 kg) في المستوى XY، بحيث يُعطى موضعه والقوة المؤثرة عليه في لحظة معينة بالمتجهين الموضحين في الشكل أدناه، حيث: F = 4 N وr = 2 m .
احسب العزم المؤثر على الجسم بالنسبة لمحور للعمودي على المستوى XY. وما هو التسارع الزاوي للجسم.
الحل
باستخدام قاعدة اليد اليُمنى يكون اتجاه العزم عمودي على مستوى XY خارج الورقة، أي باتجاه المحور Z.
من معادلة حساب العزم الدوراني، لدينا:
Ꚍ = r × F sin ϴ
Ꚍ = r × F sin 30 = 2 × 4 × 0.5 = 4 N.m
ومن معادلة القصور الدوراني، لدينا:
α = Ꚍ / I
أو:
Ꚍ = (m r2) × α
4 = 2 × (2)2 × α
a = 0.5 rad/s2
بالتقدير الدائري.





