3. العزم الدوراني

العزم الدوراني Torque #

تعريف العزم الدوراني #

عندما تؤثر قوة مقدارها F على جسم كتلته m وتجعله يتحرك حركة دورانية حول محور معين، بحيث تؤثر القوة في نقطة تبعد مسافة r عن المحورـ فيكون لهذه القوة عزم يطلق عليه عزم القوة الدوراني، وهذا العزم يتسبب في حركة الجسم حركة دائرية حول المحور. ويُرمز له بالرمز Ꚍ.

ومن أمثلة ذلك القوة التي تؤثر على باب من أجل فتحه، فكلما كانت نقطة تأثير القوة قريبة من محور دوران الباب كانت الحاجة لقوة أكبر من أجل فتحه، وكلما ابتعدنا عن محور الدوران تكون الحاجة لقوة أقل من أجل فتح الباب. الشكل التالي يوضح مقطع رأسي لهذا المثال.

قانون حساب العزم الدوراني #

تسمى المسافة بين نقطة تأثير القوة على الجسم ومحور دوران الجسم ذراع الرافعة، أو ذراع القوة. ويتم حساب العزم الدوراني حسب العلاقة الشهيرة التالية:

العزم = القوة × ذراع القوة

Ꚍ = r × F

ولكن في حالة الحركة الدورانية، يكون المطلوب احتساب حاصل ضرب مركب الاتجاه العمودي لذراع القوة r_ꓕ في القوة F، وبالتالي تصبح العلاقة كما يلي:

Ꚍ =  × F

أي أن:

Ꚍ = r sin ϴ × F

Ꚍ = r × F sin ϴ

حيث ϴ هي الزاوية التي تصنعها القوة F مع ذراع القوة r.

وهي النتيجة التي نحصل عليها عند ضرب مركب الاتجاه العمودي للقوة F_ꓕ في ذراع القوة r.

أما مركب الاتجاه الذي في نفس اتجاه القوة فليس له تأثير على العزم الدوراني ولا يتم احتسابه.

وحدة قياس عزم القوة #

من معادلة حساب العزم، يمكن استنتاج وحدة قياس عزم القوة كما يلي:

وحدة قياس عزم القوة = وحدة قياس القوة × وحدة قياس المسافة = نيوتن × متر، أو بالرموز (N.m).

اتجاه عزم القوة #

عزم القوة هي كمية فيزيائية متجهة ويتم تحديد اتجاهها باستخدام قاعدة اليد اليُمنى:

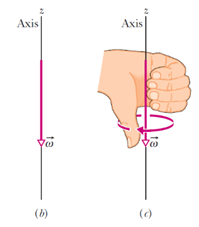
فإذا اعتبرنا أن أصابع اليد اليُمنى تُشير إلى اتجاه الدوران، فإن الإبهام سيشير إلى اتجاه العزم. مثلا لو اعتبرنا أننا نقوم بإدارة برغي باتجاه عقارب الساعة فإن اتجاه العزم سيكون عمودي على الورقة إلى الداخل.

مثال (2) #

احسب العزم الدوراني للقوتين F₁ و F₂ المؤثرتين على جسم نقطي يتحرك حركة دورانية لحظة مروره بالنقطة K حول محور دوران بمر بالنقطة C في المستوى الأفقي كما بالشكل التالي:

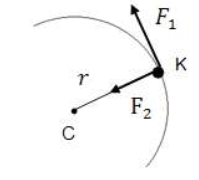
الحل

بالنسبة للقوة F₁ فهي قوة مماسية عمودية على ذراع القوة. ويكون:

Ꚍ₁ = r × F₁ sin ϴ

Ꚍ₁ = r × F₁ sin 90 = r × F₁

واتجاه العزم هو خارج الورقة حسب قاعدة اليد اليمنى.

أما بالنسبة للقوة F₂ فهي قوة مركزية باتجاه ذراع القوة، ويكون:

Ꚍ₂ = r × F₁ sin 180 = 0

ومن أجل تفسير الفرق بين القوتين واتجاه تأثيرهما وعلاقته بالعزم الدوراني، تخيل أنك تقوم بمحاولة فتح باب عن طريق دفعه بقوة F₁ من نقطة تبعد مسافة r باتجاه عمودي على ذراع القوة r كما في حالة القوة F₁ في الشكل أعلاه، وتخيل أنك تحاول فتح نفس الباب عن طريق دفعه بقوة F₂ من نقطة تبعد مسافة r ولكن باتجاه محور الدوران وكأنك تضغط عليه باتجاه الحائط، كما في حالة القوة F₂ في الشكل أعلاه، وسوف يتضح لك على الفور لماذا يتم فتح الباب في الحالة الأولى لأن هناك عزم دوراني ولا يتأثر في الحالة الثانية لأن العزم الدوراني يساوي صفر.