1. متغيرات الحركة الدورانية

متغيرات الحركة الدورانية #

تعريف الحركة الدورانية #

الحركة الدورانية هي حركة جسم بشكل دائري حول محور ثابت يُسمى محور الدوران.

يتم تحديد موضع الجسم الذي يتحرك حركة دورانية من خلال معرفة مقدار الزاوية ϴ التي يصنعها أثناء الدوران مع اتجاه ثابت مرجعي، أي الزاوية المحصورة بين المحور السيني والاتجاه الثابت.

الموضع الزاوي #

ϴ =

حيث:

• s هي الجزء من الدائرة المناظر للمسافة التي يقطعها الجسم حتى يصنع الزاوية ϴ.
• r نصف قطر الدائرة.

مع ملاحظة أن وحدة قياس الزاوية ϴ هو بالتقدير الدائري rad. حيث أن:

360 = 2π rad

الإزاحة الزاوية #

يمكن التعبير عن الإزاحة الزاوية التي يقطعها الجسم الذي يتحرك حركة دورانية من خلال حساب الزيادة في مقدار الزاوية التي يصنعها مع الاتجاه المرجعي الثابت. أي أن الإزاحة الزاوية ϴ∆ تساوي:

∆ϴ = ϴ₂ – ϴ₁

والإزاحة الزاوية هي كمية فيزيائية متجهة، وقد اعتمد أن تكون بإشارة موجبة إذا كانت الحركة عكس اتجاه عقارب الساعة، وتكون سالبة إذا كانت الحركة باتجاه عقارب الساعة.

السرعة الزاوية #

إذا افترضنا أن الجسم الذي يتحرك حركة دورانية كان يتواجد في الموضع الزاوي ϴ₁ عند الزمن t₁ ثم تواجد في الموضع الزاوي ϴ₂ عند الزمن t₂، فإنه يمكن تعريف متوسط السرعة الزاوية للجسم خلال الفترة الزمنية ∆t = t₂ – t₁ بحيث تكون:

ω _avg =

التسارع الزاوي #

إذا كانت سرعة الجسم غير ثابتة وافترضنا أن سرعته تغيرت من ω₁ إلى ω₂ في الوقت t₁ وt₂ على الترتيب، فإنه يمكن حساب متوسط التسارع الزاوي α كما يلي:

α _avg = =

والتسارع الزاوي هو كمية متجهة ويتم حساب اتجاه التسارع باستخدام قاعدة اليد اليُمنى، كما بالشكل:

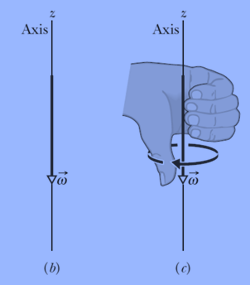
العلاقة بين متغيرات الحركة الخطية والحركة الزاوية #

عند المقارنة بين الحركة في خط مستقيم والحركة الزاوية، يمكن إيجاد العلاقة بين متغيرات الحركة الخطية (الموضع الإزاحة والسرعة والتسارع) وما يناظرها في الحركة الزاوية كما يلي:

الموضع الخطي #

موضع جسم يبعد مسافة r عن محور الدوران ويصنع زاوية مقدارها ϴ مع الاتجاه المرجعي الثابت ويقطع إزاحة القوس s من الدائرة، حيث:

s = ϴ r

السرعة الخطية #

يمكن اشتقاق السرعة الخطية عندما يتحرك الجسم حركة دورانية ويتغير موضعه بمرور الزمن كما يلي:

v =

v =  × r

v = ω r

التسارع الخطي المماسي #

في حالة تغير مقدرا السرعة الخطية للجسم المتحرك حركة دورانية، يمكن حساب التسارع الخطي المماسي للجسم a_t، ويعني التسارع الذي في اتجاه المماس (وهو التسارع الناتج عن التغير في قيمة السرعة فقط وليس الاتجاه) ويتم حسابه كما يلي:

a_t =

a_t =

a_t =

التسارع الخطي المركزي #

وهو التسارع الناتج عن التغير في اتجاه السرعة للجسم المتحرك حركة دائرية، وهو كمية متجهة واتجاهه عمودي على محور الدوران باتجاه المركز، ويمكن حسابه حسب العلاقة التالية:

a_c =

a_c =  × r (بالتقدير الدائري)