القصور الدوراني
تعريف القصور الدوراني
القصور الدوراني هو مقاومة الجسم للقوة التي تحاول إحداث تغيير في حالة حركة الجسم الدورانية، ويُرمز له بالرمز I.
نفرض أنه لدينا جسم نقطي كتلته m يتحرك حركة دورانية في مسار دائري نصف قطره r فإن القصور الدوراني يمكن حسابه من خلال العلاقة التالية:
I = m * r 2
وهو مقدار موجب دائمًا. وكذلك هو كمية قياسية وليست متجهة.
وحدة قياس القصور الدوراني
من معادلة حساب القصور الدوراني يمكن استنتاج أن:
وحدة قياس القصور الدوراني = وحدة قياس الكتلة × مربع وحدة قياس المسافة
أي أن:
وحدة قياس القصور الدوراني = كجم × متر 2، أو بالرموز: kg.m2.
القصور الدوراني لمجموعة من الأجسام
القصور الدوراني لمجموعة من الأجسام التي تتحرك حركة دورانية هو المجموع الجبري لحاصل ضرب كتلة كل جسم في مربع نصف قطر الدائرة، أي أن:
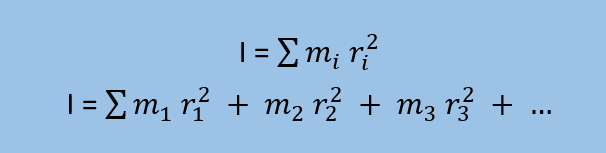
القصور الدوراني لجسم صلب كبير
يتم حساب القصور الدوراني للجسم الصلب الكبير مثل (الكرة، الأسطوانة الدائرية، سلك رفيع، .. إلخ) عن طريق حساب التكامل كما يلي:
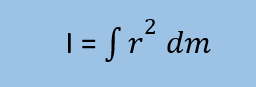
والجدول التالي يبين نتيجة حساب القصور الدوراني لبعض الأجسام الشائعة في المسائل:
| الجسم | محور الدوران | القصور الدوراني I |
| سلك رفيع طوله L | عمودي على السلك عند الطرف | 1/12 ML2 |
| عمودي على السلك عند المركز | 1/3 ML2 | |
| طوق نصف قطره R | يمر من المركز في مستواه | 1/2 MR2 |
| يمر من المركز عموديًا على مستواه | MR2 | |
| قرص رقيق مصمت نصف قطره R | يمر من المركز في مستواه | 1/4 MR2 |
| يمر من المركز عموديًا على مستواه | 1/2 MR2 | |
| كرة صلبة مصمتة نصف قطرها R | أي قطر فيها | 2/5 MR2 |
| قشرة كروية رقيقة نصف قطرها R | أي قطر فيها | 2/3 MR2 |
| أسطوانة مصمتة قائمة نصف قطرها R وطولها L | محورها الطولي | 1/2 MR2 |
مثال (1)
وُضع جسمان نقطيان كتلتاهما (5 kg)، (7 kg) على بعد (4 m) على ساق معدني خفيف مهمل الوزن، كما في الشكل التالي. احسب القصور الدوراني للنظام في حالة:
- عندما يدور حول محور في منتصف المسافة بينهما
- عندما يدور حول محور يبعد مسافة (0.5 m) إلى يسار الجسم الذي كتلته (7 kg).
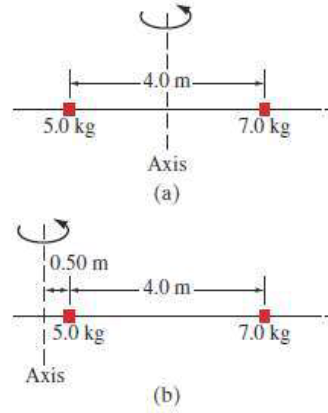
الحل
- الحالة الأولى:
I = m1 * r1 2 + m2 * r2 2
I = 5 × (2)2 + 7 × (2)2 = 48 kg.m2
- الحالة الثانية:
I = m1 * r1 2 + m2 * r2 2
I = (5) × (0.5)2 + 7 × (4.5)2 = 143 kg.m2





