
ملخص المحتوى
شرح وتبسيط مفهوم معامل الارتباط وطريقة حسابه ودلالاته، أنواع معاملات الارتباط المختلفة، معامل ارتباط بيرسون، معامل ارتباط سبيرمان، معامل ارتباط فاي أو φ، ومعامل الارتباط الخطي الجزئي. شروط استخدامها وطرق حسابها ومعادلاتها الرياضية أو قوانين حسابها واستخداماتها بالأمثلة التوضيحية المبسطة.
المحتويات
المفهوم
من أساليب التحليل الإحصائي للبيانات ما يسمى بالارتباط، والارتباط هو مفهوم إحصائي يوضح العلاقة بين متغيرين أو أكثر. ونظرًا لتعدد أنواع البيانات أو المتغيرات وحتى وحدات القياس في البحث العلمي فقد تعددت أنواع معامل الارتباط وطرق حسابها.
والهدف من استخدام هذا المعامل يكون لإيجاد العلاقة بين متغيرين، وفحص ما إذا كانت علاقة إيجابية أو سلبية (علاقة طردية أو عكسية)، قوية أو ضعيفة.
كما تأتي أهمية دراسة الارتباط من دوره في التنبؤ كطريقة من طرق الحصول على المعرفة. فإذا كان الارتباط قويًا بين متغيرين فهذا يعني إمكانية تقدير قيمة أحد المتغيرين عند معرفة القيمة المقابلة للمتغير الآخر بدقة أكبر مما لو كان الارتباط ضعيفًا.
الارتباط البسيط
يُقصد بالارتباط البسيط العلاقة بين متغيرين بصرف النظر عن نوع أي منهم من حيث نوع القياس، وأكثرها شيوعًا هو الارتباط بين متغيرين كل منهما من نوع القياس الفئوي أو من نوع القياس النسبي. ويحدد الارتباط عادة بالقوة والاتجاه (قيمة موجبة أو سالبة).
وتتلخص إجراءات تحليل الارتباط في الكشف عن قوة علاقة الارتباط واتجاهها من خلال كل من رسم شكل الانتشار وحساب قيمة معامل الارتباط، وفيما يلي تفصيل ذلك:
رسم شكل الانتشار
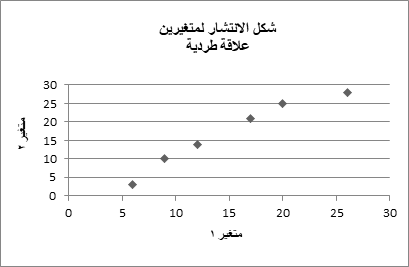
يعطي شكل الانتشار فكرة سريعة عن قوة واتجاه علاقة الارتباط بين متغيرين، فيتم تحديد قيم أحد المتغيرين على المحور الأفقي والمتغير الآخر على المحور الرأسي. وتحدد النقاط التي تشكل أزواج القيم إحداثياتها. والشكل الناتج بعد تحديد جميع النقاط هو شكل الانتشار.
وحتى يتضح معنى قوة العلاقة لا بد من مقارنة الشكل الناتج بشكل انتشار معين. فإذا كانت جميع النقاط واقعة على خط مستقيم فهذا يعني أن العلاقة تامة سواء كانت علاقة طردية أو عكسية.
مثلا، الشكل التالي يوضح شكل الانتشار لمتغيرين مرتبطين بعلاقة طردية:
حساب قيمة المعامل
يعتبر معامل الارتباط مؤشرًا كميًا على قوة العلاقة واتجاهها بين متغيرين، إذ يمكن أن يأخذ أي قيمة بين –1، 1. حيث تدل القيمة المحسوبة على قوة العلاقة وتدل الإشارة على اتجاهها، موجبة أو سالبة.
وتتعدد أنواع معاملات الارتباط حسب تعدد أنواع المتغيرات، فقد يكون الارتباط بين متغيرين كل منهما اسميًا، أو رتبيًا أو فئويًا، وربما كان خليطًا من هذه المتغيرات.
دلالة معامل الارتباط
في التحليل الإحصائي للبيانات يُشير معامل الارتباط إلى قوة واتجاه العلاقة بين متغيرين، ولكن هذه العلاقة لا تُفسَّر على أنها علاقة سببية، مع أنها يمكن أن تكون كذلك.
ويمكن فحص معامل الارتباط بمقارنته بمعيار مُتفق عليه للعلاقة بين المتغيرات موضوع البحث. وقد جرى تصنيف قيم معامل الارتباط إلى (ضعيفة، متوسطة، قوية) إذا وقعت ضمن المدى (صفر-0.39)، (0.40-0.69)، (0.70-1.00) على الترتيب. ولكن هذه ليست قاعدة تُتبع دائمًا، فهذا أمر متروك للباحث على ضوء ما هو معروف عن العلاقة بين المتغيرات الواردة في البحث.
ومعامل الارتباط هو المؤشر الكمي على قوة العلاقة واتجاهها بين متغيرين، ويمكن أن يأخذ أي قيمة بين القيمتين (–1، 1)، حيث تدل قيمته المحسوبة على قوة العلاقة بين المتغيرين وتدل الإشارة على اتجاهها وما إذا كانت علاقة طردية (القيم الموجبة) أو علاقة عكسية (القيم السالبة).
أنواع معامل الارتباط
تتعدد أنواع معامل الارتباط بحسب تعدد أنواع البيانات أو المتغيرات التي يتم بحث أو تحليل الارتباط فيما بينها.
فقد يكون الارتباط بين متغيرين كل منهما اسميًا أو رتبيًا أو فئويًا، أو حتى خليطًا من هذه الأنواع، وبالتالي يختلف المعامل الذي يمكن استخدامه بحسب نوع وطبيعة تلك البيانات والمتغيرات.
وتوجد أربعة أنواع من معاملات الارتباط وهي:
- معامل ارتباط بيرسون أو Pearson
- ومعامل ارتباط سبيرمان أو Spearman
- معامل ارتباط فاي أو φ
- معامل الارتباط الخطي الجزئي
وتُعتبر هذه الأنواع الأربعة هي الأكثر استخدامًا في مجالات البحث العلمي وتحليل البيانات أو تنقيب البيانات بشكل عام.
وفيما يلي وصفًا موجزًا لكل منها، مع شرح شروط استخدامها ومعادلة أو قانون حسابها مع الأمثلة التطبيقية:
معامل ارتباط بيرسون Person’s Coeff
معامل ارتباط بيرسون أو معامل بيرسون هو معامل الارتباط بين متغيرين كل منهما من نوع البيانات المتصلة. وقد سُمي بهذا الاسم نسبة إلى العالم البريطاني كارل بيرسون الذي وضع أسس الإحصاء الرياضي.
وعند حساب معامل بيرسون فإنه يفترض أن العلاقة بين المتغيرين علاقة خطية، ويُفضل رسم شكل الارتباط للتأكد من ذلك قبل حساب هذا المعامل.
قانون حساب معامل بيرسون للارتباط
يمكن استخدام المعادلة التالية أو قانون حساب معامل بيرسون للارتباط لحساب قيمة المعامل كما يلي:
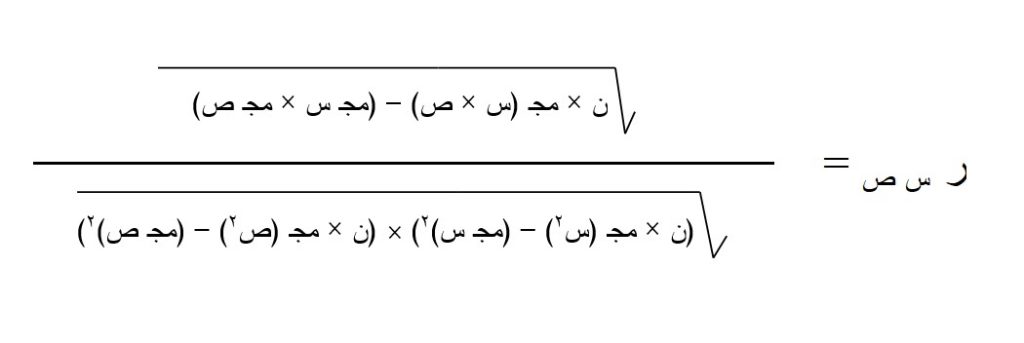
مثال تطبيقي على معامل ارتباط بيرسون
المثال التالي يوضح خطوات حساب معامل بيرسون للارتباط، باستخدام القانون، بين عدد مرات شراء الزبون لمنتجات أحد المراكز التجارية (س) وتقييمه لهذه المنتجات (ص)، وعدد الزبائن في هذا المثال هو (ن).
بعد حساب كل من س2 و ص2 و (س × ص) نحصل على الجدول التالي:
| س × ص | ص2 | س2 | ص | س |
| 12 | 9 | 16 | 3 | 4 |
| 150 | 100 | 225 | 10 | 15 |
| 48 | 36 | 64 | 6 | 8 |
| 56 | 49 | 64 | 7 | 8 |
| 24 | 16 | 36 | 4 | 6 |
فيكون لدينا:
مجـ (س) = 41
مجـ (س2) = 405
و (مجـ س) 2 = 1681
مجـ (س × ص) = 290
مجـ (ص) = 30
و مجـ (ص 2) = 210
(مجـ ص) 2 = 900
بالتعويض في قانون حساب معامل بيرسون، فإنه ينتج لدينا:
ر س ص = الجذر التربيعي لـ (1450-1230) / ( (2025-1681) × (1050-900) )
ر س ص = 0.97 مقربًا لأقرب رقمين أو منزلتين عشريتين.
أي أن هناك علاقة ارتباط قوية بين عدد مرات شراء الزبون للمنتج وتقييمه له.
معامل ارتباط سبيرمان Spearman’s Coeff
معامل ارتباط سبيرمان (أو معامل سبيرمان) هو معامل الارتباط بين متغيرين كل منهما من بيانات النوع الرتبي.
ويُعتبر معامل سبيرمان للارتباط صورة أخرى من معامل بيرسون. فإذا كانت البيانات الإحصائية واقعة فعلا على مقياس رتبي أو أقرب إلى الرتبي منه إلى الفئوي فإن المعامل المناسب للاستخدام هو معامل سبيرمان ρ (رو).
يصادف الباحث أحيانًا تشابهًا في رتب بعض البيانات للمتغير الواحد، وكلما زادت الرتب المشاركة كلما قلت دقة المعامل المحسوب بهذا المعامل.
قانون حساب معامل سبيرمان للارتباط
يمكن استخدام المعادلة التالية أو قانون حساب معامل سبيرمان للارتباط يدويًا لحساب قيمته كما يلي:
ρ (رو) = 6 × ( مجـ ف 2 ) / ن × (ن 2 – 1)
حيث أن: ف = فروق الرتب.
مثال على معامل سبيرمان
المثال التالي يوضح حساب الارتباط بين رتب تقييم عدد (6) زبائن للمنتج (س)، ورتب تقييمهم للمنتج (ص):
| ف 2 | ص | س |
| 1 | 2 | 1 |
| 1 | 5 | 6 |
| 2.25 | 3.5 | 5 |
| 0.25 | 3.5 | 3 |
| 1 | 1 | 2 |
| 4 | 6 | 4 |
| مجـ (ف 2) = 9.5 |
بالتعويض في قانون حساب معامل سبيرمان، يتم بالتالي الحصول على:
ρ (رو) = 6 × (مجـ ف 2) / ن (ن 2 – 1)
وبالتعويض عن القيم يكون:
ρ (رو) = 6 × (9.5) / 6 × (36 – 1)
أي أن:
ρ (رو) = 0.73 (مقربًا لرقمين أو لمنزلتين عشريتين).
أي أن هناك علاقة ارتباط قوية بين تقدير الزبائن للمنتج (س) وتقديرهم للمنتج (ص).
معامل ارتباط فاي φ
معامل ارتباط فاي φ هو معامل الارتباط بين متغيرين كل منهما منفصل ثنائي، بمعنى أن كل منهما متغيرًا من النوع الاسمي ولكل متغير مستويين فقط. ولذلك لا يصلح هذا المعامل إذا كان لأحد المتغيرين أو لكليهما أكثر من مستويين.
قانون حساب معامل ارتباط فاي
المعادلة العامة أو قانون حساب معامل الارتباط فاي φ هو:
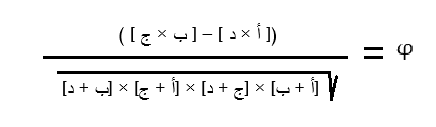
مثال على معامل ارتباط فاي φ
في المثال التالي عينة من عشرة أفراد من الجنسين تم اختيارهم لتقدير العلاقة بين جنس الأفراد ومدى قبولهم أو رضاهم عن الخدمات التي يقدمها أحد البنوك:
الخطوة الأولى: تمييز عناصر كل متغير بشيفرة معينة، كأن يعطي الجنس (ذكر، أنثى) أو الأرقام (1، 0) على الترتيب، وتقييمهم للخدمات التي يقدمها البنك (قبول، رفض) أو الأرقام (1، 0) على الترتيب.
والأرقام هنا ليس لها معنى كمي ولذلك يمكن أن يُصطلح على أي رقم أو رمز. ثم تبوب البيانات في جدول كالتالي:
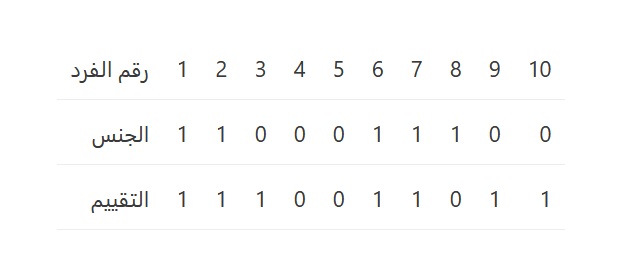
والآن لحساب معامل ارتباط فاي φ يلزم تجميع هذا الجدول على شكل اقتران ثنائي (أو دالة ثنائية) البعد كما يلي:
| المجموع | رفض | قبول | |
| أ + ب = 5 | ب = 1 | أ = 4 | ذكر |
| ج + د = 5 | د = 2 | ج = 3 | أنثى |
| أ + ب + ج + د = 10 | ب + د = 3 | أ + ج = 7 | المجموع |
حيث تشير الرموز في الخلايا إلى عدد العناصر الناتجة من تقاطع فئات المتغيرين، فمثلا (أ = 4)، وهذا يعني أن عدد الذكور الذين اعتبروا أن خدمات البنك مقبولة هو 4.
وبتطبيق هذه المعادلة على المثال، يكون:
فاي () = (8 – 3) / الجذر التربيعي لـ (5 × 5 × 7 × 3)
فاي () = 0.22 مقربًا لمنزلتين عشريتين.
بمعنى أن هناك ارتباطًا ضعيفًا بين موقف الأفراد من الخدمات التي يقدمها البنك وجنسهم، إلا أن إشارة الارتباط موجبة، بمعنى أن الذكور يميلون إلى قبول هذه الخدمات أكثر من الإناث.
معامل الارتباط الخطي الجزئي
يُستخدم معامل الارتباط الخطي الجزئي في حالة وجود ثلاث متغيرات. وهو يقيس درجة العلاقة بين متغيرين اثنين بعد تثبيت أثر المتغير الثالث.
مثال على معامل الارتباط الخطي الجزئي
مثلا، لقياس درجة العلاقة بين الوزن والطول بعد تثبيت أثر اختلاف الأعمار على كل من الوزن والطول يوجد طريقتين:
الطريقة الأولى
نختار أفراد العينة من عمر واحد، وبذلك فإن الوزن سوف يتحدد على أساس الطول فقط.
الطريقة الثانية
نستخدم معامل الارتباط الخطي الجزئي والذي يُحسب باستخدام المعادلة أو القانون التالي:
قانون حساب معامل الارتباط الخطي الجزئي
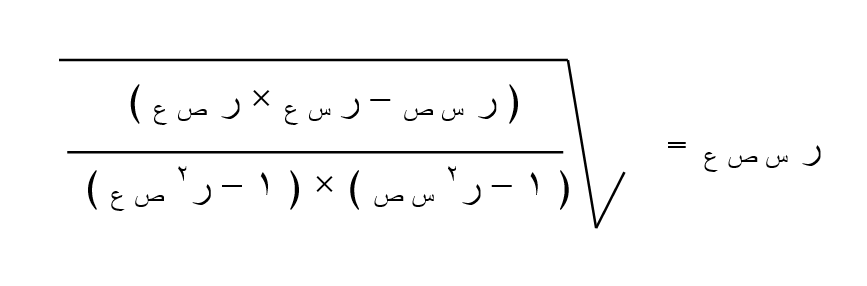
حيث ر س ص ، ر س ع ، ر ص ع هي معاملات الارتباط الخطية البسيطة بين (س، ص)، (س، ع)، (ص، ع) على الترتيب.
مع ملاحظة أنه إذا كان المتغيرين س، ص كلاهما متغير مستقل عن المتغير الثالث ع فإن:
ر س ع = ر ص ع = صفر.
اختيار المعامل المناسب
يتضح من شرح أنواع معاملات الارتباط واستخداماتها أنه يختلف باختلاف أنواع البيانات أو المتغيرات التي يهدف المعامل لإيجاد العلاقة بينها، ولذلك فإنه يلزم لاختيار وتحديد نوع المعامل المناسب الفهم المتعمق لطبيعة البيانات والمتغيرات التي يتم دراستها.
موضوع مقترح: المتغيرات في البحث العلمي – أنواعها واستخداماتها
موسوعة البحث العلمي – مركز البحوث والدراسات متعدد التخصصات
المصدر
- كتاب مهارات البحث العلمي، د.م. مصطفى فؤاد عبيد، مركز البحوث والدراسات متعدد التخصصات، الطبعة الثانية، إسطنبول، تركيا، 2022م.
- كتاب التحليل المتقدم وتنقيب البيانات، د. م. مصطفى فؤاد عبيد، دار الفكر العربي، القاهرة، جمهورية مصر العربية، الطبعة الأولى، 2017م.