2. أنواع التصادمات

أنواع التصادمات #

هناك أنواع مختلفة للتصادمات، حيث تتأثر التصادمات بعدة عوامل، منها ما إذا كان النظام الذي حدث فيه التصادم معزول ميكانيكيًا ومدى إمكانية تطبيق قانون حفظ الزخم والتغير في طاقة الوضع وطاقة الحركة للأجسام المتصادمة، وكذلك طبيعة القوى المؤثرة أثناء التصادم.

مثال توضيحي #

في الشكل التالي يوضح تجربة تبين اختلاف نتيجة تصادم عدة كرات مصنوعة من الحديد والزجاج والمطاط والمعجون عند سقوطها من ارتفاع معين على سطح صلب أملس، وذلك باختلاف الارتفاع الذي ترتد إليه الكرات بعد التصادم.

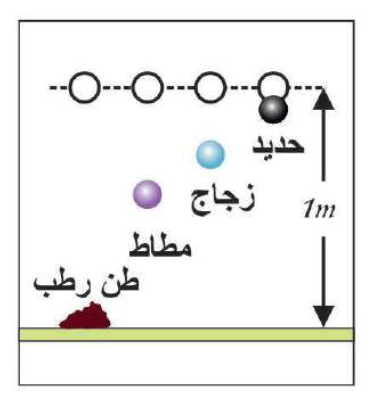
علاقة التصادم بطاقة الوضع وطاقة الحركة #

إن النقص في طاقة وضع كل كرة من الكرات بين الارتفاع الذي سقطت منه والارتفاع الذي ارتدت إليه يمثل مقدار الطاقة الحركية التي فقدتها الكرة نتيجة التصادم، وذلك حسب قانون حفظ الطاقة.

يسمى التصادم تصادم مرن في حالة عدم وجود أي نقص في طاقة الحركة نتيجة التصادم. أما في حالة وجود نقصان في طاقة الحركة فيكون التصادم غير مرن.

وإذا التحم الجسمان معًا وتحركا كجسم واحد بعد التصادم تكون حالة خاصة من التصادم غير المرن وتسمى حالة تصادم عديم المرونة.

التصادم المرن Elastic Collision #

“التصادم المرن هو تأثير متبادل بين جسمين (أو أكثر) أحدهما على الأقل متحرك، بحيث يتحرك كل منهما بشكل منفرد قبل والتصادم وبعده، ويتحقق فيه قانونا حفظ الزخم وحفظ الطاقة الحركية قبل وبعد التصادم”.

ويكون التغير في الزخم P يساوي:

 = P _f – P _i

بالنسبة للجسم الأول:

 ₁ = P _1f – P _1i

وبالنسبة للجسم الثاني:

 ₂ = P _2f – P _2i

وبالتعويض عن قيمة الدفع P = m v يكون:

 ₁ = m₁ v 1f – m₁ v _1i

 ₂ = m₂ v _2f – m₂ v _2i

حيث أن:

v _1f: سرعة الجسم الأول قبل التصادم مباشرة

v _1i: سرعة الجسم الأول بعد التصادم مباشرة

v _2f: سرعة الجسم الثاني قبل التصادم مباشرة

v _2i: سرعة الجسم الثاني بعد التصادم مباشرة

وبحسب قانون نيوتن الثالث، لكل فعل رد فعل مساوِ له في المقدار ومضاد له في الاتجاه، يكون:

F ₂₁ = – F ₁₂

وحيث أن الصيغة العامة لقانون نيوتن الثاني:

وبالتعويض عن القوة، يكون:

وبضرب طرفي المعادلة في t∆ ينتج لنا أن مجموع التغير في الزخم لكلا الجسمين يكون مساويًا للصفر:

أي أن:

m₁ v _1f – m₁ v _1i + m₂ v _2f – m₂ v _2i = 0

ومنها يكون:

m₁ v 1f + m₂ v 2f = m₁ v _1i + m₂ v _2i

وهذه المعادلة تعني أنه في النظام المعزول ميكانيكيًا يكون الزخم للنظام قبل التصادم P_Initial مباشرة يساوي الزخم له بعد التصادم مباشرة P_Final.

كذلك فإن مجموع الطاقة الحركية للجسمين قبل التصادم K_Initial يساوي مجموع الطاقة الحركية للجسمين بعد التصادم مباشرة K_Initial. وهذا يعني تطبيق قانون حفظ طاقة الحركة للنظام قبل وبعد التصادم.

أي أن:

1/2 m₁ v²_1i + 1/2 m₂ v²_2i = 1/2 m₁ v²_1f + 1/2 m₂ v²_2f

وتًستخدم المعادلات السابقة لإيجاد سرعة الجسمين المتصادمين بعد التصادم مباشرة.

السرعة النسبية للجسمين المتصادمين #

من المعادلات السابقة يمكن استنتاج أنه في حالة التصادم المرن في بُعد واحد تكون:

v_1i – v_2i = – (v_1f – v_2f)

أو بالاختصار:

v_12i = – (v_12f)

وهو ما يعني أن السرعة النسبية للجسمين قبل التصادم تساوي السرعة النسبية للجسمين بعد التصادم في المقدار وتعاكسها في الاتجاه.

حيث:

v_12i تعني سرعة الجسم الأول بالنسبة للجسم الثاني قبل التصادم مباشرة.

v_12f تعني سرعة الجسم الأول بالنسبة للجسم الثاني بعد التصادم مباشرة.

مثال (1) #

جسم كتلته (4 kg) يتحرك لليمين بسرعة (2 m/s) اصطدم بجسم آخر كتلته (2 kg) يتحرك في اتجاه معاكس وبنفس السرعة. احسب سرعة كل من الجسمين بعد التصادم مباشرة إذا كان التصادم مرنًا.

الحل

بما أنه لدينا من قانون حفظ الزخم:

m₁ v _1i + m₂ v _2i = m₁ v _1f + m₂ v _2f

4 × 2 + 2 × (- 2) = 4 v _1f + 2 v _2f

2 = 2 v _1f + v _2f

v _2f = 2 – 2 v _1f

وكذلك لدينا:

v_1i – v_2i = – (v_1f – v_2f)

v_1i – v_2i = v_2f – v_1f

بالتعويض عن جميع القيم:

2 – (-2) = [ 2 – 2 v _1f] – v_1f

4 = 2 – 3 v_1f

v_1f = -2/3 m/s

v_2f = 10/3 m/s

التصادم غير المرن Inelastic Collision #

يكون التصادم غير مرن عندما يفقد النظام من طاقته الحركية قبل التصادم، حيث تتحول هذه الطاقة إلى أشكال أخرى مثل الصوت أو التشوهات التي تحدث للأجسام المتصادمة.

وكغيره من أنواع التصادمات، يحقق التصادم غير المرن قانون حفظ الزخم.

أي أن:

m₁ v _1i + m₂ v _2i = m₁ v _1f + m₂ v _2f

إذا تصادم جسمين أو أكثر فإن المجموع الاتجاهي للزخم قبل التصادم يساوي المجموع الاتجاهي للزحم بعد التصادم.

والتغير في طاقة الحركة للنظام قبل وبعد التصادم يكون:

∆K = K_f – K_i = [1/2 m₁ v²_1f + 1/2 m₂ v²_2f]-[1/2 m₁ v²_1i + 1/2 m₂ v²_2i]

مثال (2) #

تتحرك كرة كتلتها (2 kg) باتجاه الغرب بسرعة مقدارها 6 m/s، فتصطدم بكرة أخرى كتلتها (3 kg) تتحرك باتجاه الشرق بسرعة 4 m/s. إذا أصبحت سرعة الكرة الأولى مباشرة بعد التصادم 4.5 m/s. كما في الشكل حيث بقي الجسمان يتحركان على نفس الخط قبل وبعد التصادم، ودام التصادم 0.02 ثانية. احسب:

1. سرعة الكرة الثانية بعد التصادم مباشرة
2. متوسط القوة التي أثرت بها الكرة الأولى على الثانية أثناء التصادم
3. وحدد نوع التصادم

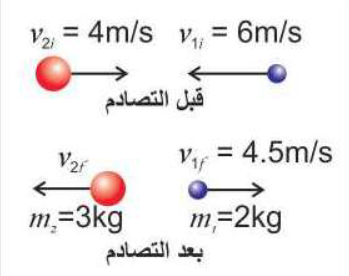
الحل

1. من قانون حفظ الزخم قبل وبعد التصادم، لدينا:

m₁ v _1i + m₂ v _2i = m₁ v _1f + m₂ v _2f

بالتعويض عن القيم المُعطاة:

2 × (-6) + 3 × (4) = 2  ×(4.5) + 3 v _2f

v _2f = – 3 m/s

• الدفع على الكرة الثانية يساوي التغير في الزخم ∆P₂:

F ∆t = ∆P₂

F ∆t = m₂ v _2i – m₂ v _2f

F × (0.02) = 3 (-3 – 4)

F = – 1050 N

• لتحديد نوع التصادم، نحسب طاقة الحركة قبل وبعد التصادم:

K_i = [1/2 m₁ v²_1i + 1/2 m₂ v²_2i]

K_i = [1/2 × 2 × 36+ 1/2 × 3 × 16] = 60 J

K_f = [1/2 m₁ v²_1f + 1/2 m₂ v²_2f]

K_f = [1/2 × 2 × 20.25 + 1/2 × 3 × 9] = 33.75

∆K =

∆K = 33.75 – 60 = – 26.25 J

الفرق في طاقة الحركة بإشارة سالبة يعني أن النظام فقد طاقة حركة، ويكون بالتالي هو تصادم غير مرن لأن الجسمان تحركا بشكل منفرد بعد التصادم.

التصادم عديم المرونة Completely Inelastic Collision #

عندما يصطدم جسمان ويلتحمان معًا ويتحركان كجسم واحد بعد التصادم ويصبح لهما سرعة واحدة، وتظل كمية التحرك محفوظة بينما يحدث نقصان للطاقة الحركية وهذا النقص يتحول إلى أشكال أخرى للطاقة، فإن هذا التصادم يسمى تصادم عديم المرونة.

ومن أمثلة التصادم عديم المرونة تصادم السهم مع قرص التصويب المعلق عندما يستقر فيه.

بتطبيق قانون حفظ الزخم للجسمين قبل وبعد التصادم:

مجموع الزخم للجسمين قبل التصادم = مجموع الزخم للجسمين بعد التصادم

m₁ v _1i + m₂ v _2i = (m₁ + m₂) (v _f)

حيث أن v _f هي سرعة الجسمين معًا بعد التصادم.

والتغير في طاقة الحركة للنظام قبل وبعد التصادم يكون:

∆K = K_f – K_i = [1/2 (m₁ + m₂) × v²_f] – [1/2 m₁ v²_1i + 1/2 m₂ v²_2i]

مع ملاحظة أن النقصان في طاقة الحركة يعني أنه تحول إلى شكل آخر من أشكال الطاقة، وذلك بحسب قانون حفظ الطاقة والذي ينص على أن :الطاقة لا تُفنى ولا تُستحدث من عدم”.

مثال توضيحي #

من الأمثلة الشهيرة على التصادم عديم المرونة هو البندول القذفي البسيط الذي يُستخدم في حساب سرعة اصطدام رصاصة تستقر في قطعة خشبية معلقة. وهو يتكون من كتلة خشبية معلقة بحبلين متساويين متوازيين غير مرنين، حيث تكون الكتلة الخشبية أكبر بكثير من كتلة الرصاصة.

وفي هذه الحالة فإن الطاقة الحركية المفقودة تتحول إلى طاقة وضع يمكن حسابها بمعرفة الارتفاع الذي تصل إليه المجموعة (القطعة الخشبية مع الرصاصة) بعد التصادم، حيث يكون:

طاقة الوضع = m g h

حيث:

m مجموع كتلة المجموعة (الكتلة الخشبية والرصاصة)

h هو أقصى ارتفاع تصل إليه المجموعة.

g تسارع الجاذبية الأرضية (9.8 m/s²).

مثال (3) #

أُطلقت رصاصة كتلتها (30 g) على كتلة خشبية كتلتها (4.97 kg) معلقة كما في الشكل المقابل، فكان أقصى ارتفاع رأسي وصلت إليه المجموعة هو (8 cm) عن المستوى الأفقي الأصلي. احسب كل من:

1. سرعة المجموعة بعد التصادم مباشرة
2. سرعة الرصاصة قبل الاصطدام مباشرة
3. مقدار الطاقة الحركية المفقودة

الحل

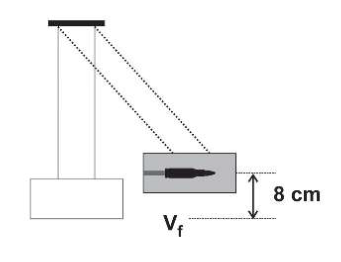
1. من قانون حفظ الطاقة الميكانيكية، فإن مقدار طاقة الحركة للمجموعة بعد التصادم مباشرة يساوي مقدار طاقة الوضع المكتسبة. أي أن:

m g h = 1/2 m v_f²

حيث m = m₁ + m₂

بالتعويض ينتج أن:

m g h = 1/2 m v_f²

g h = 1/2 v_f²

v_f =  = 1.26 m/s

• من قانون حفظ الزخم:

m₁ v_1i + m₂ v _2i = (m₁ + m₂) (v _f)

0.3 × v_1i + m₂ × 0 = (4.97 + 0.3) × (1.26)

v_1i = 210 m/s

1. مقدار الطاقة الحركية المفقودة:

∆K = K_f – K_i = [1/2 (m₁ + m₂) × v²_f] – [1/2 m₁ v²_1i + 1/2 m₂ v²_2i]

بالتعويض ينتج أن:

∆K = [1/2 (4.97 + 0.3) × 1.26²] – [1/2 × 0.3 × 210²]

∆K = 4 – 661.5 Kg.m²/s² = – 657.5 J