التصادم في بُعدين
تعريف التصادم في بُعدين
التصادم في بُعدين هو التصادم الذي لا تتحرك فيه الأجسام المتصادمة في خط مستقيم قبل وبعد التصادم أو لا تبقى على نفس الخط المستقيم قبل وبعد التصادم. ومن أمثلتها تصادم كرات البلياردو حيث تتحرك قبل وبعد التصادم بشكل يصنع زوايا فيما بينا وليس في خط مستقيم.
قانون حفظ الزخم في التصادم في بُعدين
مثل كل أنواع التصادمات، يتحقق قانون حفظ الزخم في التصادم في بُعدين في كلا الاتجاهين (السيني والصادي).
بتطبيق قانون حفظ الزخم للجسمين قبل وبعد التصادم:
مجموع الزخم للجسمين قبل التصادم = مجموع الزخم للجسمين بعد التصادم
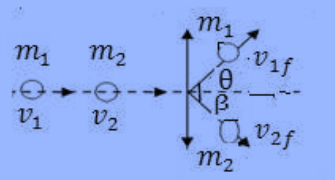
على المحور السيني:
m1 v1ix + m2 v2ix = m1 v1fx + m2 v2fx
وبمعرفة الزوايا التي يصنعها كل جسم مع المحور السيني بعد التصادم، يمكن إعادة كتابة معادلة حفظ الزخم كما يلي:
m1 v1ix + m2 v2ix = m1 v1f cos ϴ + m2 v2f cos β
وعلى المحور الصادي:
m1 v1iy + m2 v2iy = m1 v1fy + m2 v2fy
m1 v1iy + m2 v2iy = m1 v1f sin ϴ + m2 v2f sin β
قانون حفظ طاقة الحركة في التصادم في بُعدين
بالنسبة لقانون حفظ الطاقة الحركية في حالة التصادم في بُعدين فإنه يعتمد على نوع التصادم من حيث ما إذا كان التصادم مرن أو غير مرن أو عديم المرونة. والتغير في طاقة الحركة للنظام قبل وبعد التصادم يكون كما يلي:
∆K = Kf – Ki
∆K = [1/2 m1 v21f + 1/2 m2 v22f]-[1/2 m1 v21i + 1/2 m2 v22i]
وفي حالة إذا التحم الجسمان بعد التصادم مباشرة، يتم التعامل مع الجسم الناتج وكأن كتلته تساوي m = m1 + m2 وتطبيق نفس المعادلات.
مثال (1)
اصطدمت سيارة تتحرك نحو الشرق بسرعة مقدارها (13 m/s) بسيارة أخرى مماثلة لها في الكتلة تتحرك باتجاه الشمال عند مفترق طرق فالتحمت السيارتان معًا وتحرك الحطام باتجاه زاوية مقدارها 55 درجة شمال الشرق. وعندما جاء شرطي المرور ادعى سائق السيارة المتجهة شمالاً أن سرعته لم تتجاوز 60 km/h. هل ما قاله السائق يطابق ما توصل إليه شرطي المرور عند معاينة الحادث؟
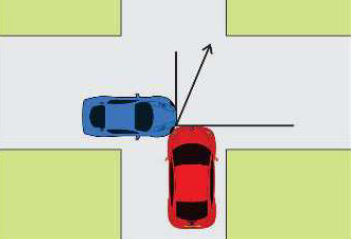
الحل
من قانون حفظ الزخم في الاتجاه السيني:
m1 v1ix + m2 v2ix = m1 v1fx + m2 v2fx
وبمعرفة أن السيارة الأولى كتلتها m تصنع زاوية مقدارها صفر مع المحور السيني، والسيارة الثانية كتلتها m أيضًا وتصنع زاوية مقدارها (90 درجة) مع المحور السيني، وحطام السيارتين معًا كتلته 2m ويصنع زاوية مقدارها (55 درجة) مع المحور السيني، فيكون:
m × 13 cos (0) + m × v2 cos (90) = (2m) × vf cos(55)
13 + 0 = 2 vf cos (55)
vf = 11.33 m/s
وفي الاتجاه الصادي:
m1 v1iy + m2 v2iy = m1 v1fy + m2 v2fy
أي أن:
m v1i sin (0) + m v2i sin (90) = (2m) vf sin(55)
0 + v2i = 2 × vf sin(55)
بالتعويض عن سرعة الحطام vf ينتج أن:
v2i = 2 × 11.33 × sin(55)
v2i = 18.56 m/s = 18.56 × 3600 / 1000 km/h = 66.8 km/h
أي أن سرعة السيارة الثانية بعد التصادم تساوي 66.8 k/h وهي لا تطابق ما ادعاه السائق.





