5. تطبيقات هندسية وفيزيائية

أولًا: تطبيقات هندسية #

تعريف ميل المنحنى #

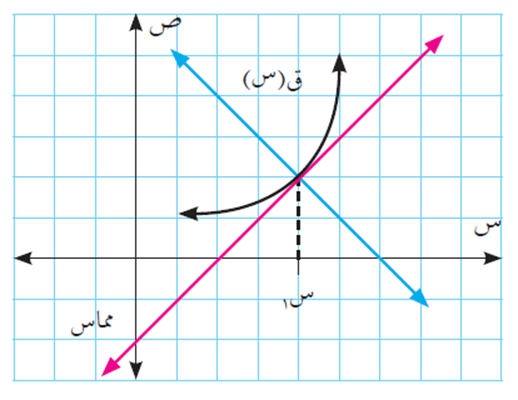
إذا كان ق(س) اقتران قابل للاشتقاق عند النقطة أ (س_١ ، ق(س₁))، فإن ميل منحنى الاقتران ق(س) عند النقطة أ هو ميل المماس المرسوم لمنحنى هذا الاقتران عند تلك النقطة، وهو يساوي مشتقة الاقتران عند نفس النقطة، أي أنه يساوي = ق^/(س₁).

ويعرف المستقيم العمودي على منحنى الاقتران، بأنه المستقيم العمودي على المماس للمنحنى عند نقطة التماس.

مثال (1) #

جد ميل منحنى الاقتران ق(س) = س^٣ + ٥ س عند س = ١، ثم جد معادلتي المماس والعمودي على المماس عند تلك النقطة.

الحل

من التعريف، يكون ميل منحنى الاقتران ق(س) عند س = ١ يساوي ميل المماس = ق^/(1).

المشتقة ق^/(س) = ٣س^٢ + ٥، ومنها ق^/(1) = 8 = ميل المماس.

لكن نقطة التماس هي (١، ق(1)) = (١، ٦)

وبمعرفة ميل المماس ونقطة التماس، يمكن إيجاد معادلة المماس، حيث يكون لدينا:

ص – ص ₁ = م (س – س ₁)

أي: ص – ٦ = ٨ × (س – ١)، ومنها يكون: ص = ٨ س – ٢

ميل العمودي على المماس = – 1 / ميل المماس

وبالمثل، يمكن إيجاد معادلة العمودي على المماس:

ص – ص ₁ = م (س – س ₁)، وبالتعويض تكون معادلة العمودي على المماس هي:

٨ص + س – ٤٩ = ٠

مثال (2) #

إذا كان المماس لمنحنى ق(س) = ٤ / س، س > صفر، يصنع زاوية قياسها ١٣٥° مع الاتجاه الموجب لمحور السينات، أثبت أن العمودي على المماس عند نقطة التماس لمنحنى ق(س) يمر بالنقطة (صفر، صفر).

الحل

نفرض نقطة التماس هي أ (س ₁، ص ₁)

ميل المماس = ظا ١٣٥ = – ١

ق^/(س) = – 4 / س^٢

لكن ميل المنحنى عند س _١ = – 4 / س _١ ²

ومنها – ١= – 4 / س _١ ²

إذن س _١ = ٢ لأن س _١ > صفر.

نقطة التماس هي (٢، ٢)، ومنها ميل العمودي = – ١ / – 1 = 1

معادلة العمودي هي:

ص – ٢ = 1 × (س – ٢) ومنها ص = س

النقطة (صفر، صفر) تقع على العمودي على المماس.

أي أن العمودي على المماس يمر بالنقطة (صفر، صفر).

مثال (3) #

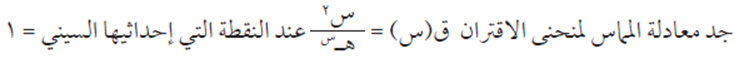
الحل

مثال (4) #

إذا كان المستقيم ص = – ٣ س + جـ يمس منحنى الاقتران ق(س) = – ٢س^٢ + ٥ س + ١.

جد نقطة/ نقط التماس.

الحل

نفرض أن نقطة التماس هي (س₁، ص₁)

ق^/(س) = – 4 س + 5

وبما أن ميل المماس = ميل المنحنى عند نقطة التماس (س₁)

إذن – 3 = – 4 س_١ + 5 ومنها س ₁ = 2

فتكون نقطة التماس = (2، ق(2)) = (2، 3)

لأن ق(2) =  – 2 ×  ²2 + 5 × 2 + 1 = 3

مثال (5) #

إذا كان المستقيم ص = جـ س + ٥ يمس منحنى الاقتران ق(س) = أ س^٣ + ب س^٢ عند النقطة (- ١، -٣)، جد قيم أ ، ب ، جـ.

الحل

النقطة (-1، – ٣) تحقق معادلة المستقيم، ومنها – ٣ = جـ × – 1 × + ٥

– 8 = – جـ

أي أن جـ = 8 ومنها ص = 8 س + 5

لكن النقطة (-1، -3) تحقق معادلة المنحنى أيضًا، أي أن:

– ٣ = أ × (-1)³ + ب × (-1)²

– ٣ = – أ + ب معادلة رقم (1)

كما أن ميل المماس = ميل المنحنى عند النقطة (- ١،  – ٣)

ومنها يكون: ٣ أ س^٢ + ٢ ب س | _{س = – ١} = ٨

 ومنها:

٣ أ – ٢ ب = ٨ معادلة رقم (2)

وبحل المعادلتين (1) و(2) ينتج أن: أ = ٢، ب = – ١.

ثانيًا: تطبيقات فيزيائية #

السرعة المتوسطة #

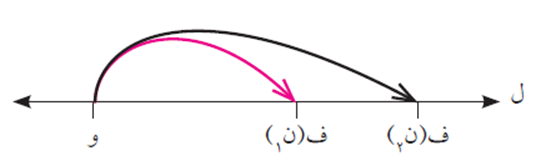
لتكن (و) نقطة على المستقيم ل وتحرك جسم عليه بحيث كانت ف تمثل بعد الجسم عن النقطة (و) بعد ن ثانية فإنه يكون:

السرعة المتوسطة في الفترة [ن_١ ، ن_٢] تساوي:

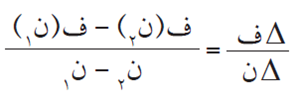
السرعة اللحظية والتسارع اللحظي #

بما أن السرعة اللحظية هي معدل تغير المسافة بالنسبة للزمن، فإنه يمكن تعريف السرعة اللحظية بأنها مشتقة المسافة بالنسبة للزمن.

وبما أن التسارع اللحظي هو معدل تغير السرعة بالنسبة للزمن، فإنه يمكن تعريف التسارع اللحظي بأنه مشتقة السرعة بالنسبة للزمن، أي أنه يساوي مشتقة (مشتقة المسافة بالنسبة للزمن)، أو المشتقة الثانية للمسافة بالنسبة للزمن. ويمكن التعبير رياضيًا عن ذلك كما يلي:

مثال (6) #

تحرك جسم على خط مستقيم، بحيث إن بعده عن نقطة ثابتة (و) يتحدد بالعلاقة: ف = ن^٣ – ٩ن^٢ + ٧ حيث ف المسافة بالأمتار، ن الزمن بالثواني، جد:

1. السرعة المتوسطة للجسم في الفترة [١ ، ٣].
2. تسارع الجسم عندما يعكس الجسم من اتجاه حركته.

الحل

لدينا: ف = ن^٣ – ٩ ن٢ + ٧1. السرعة المتوسطة تساوي:

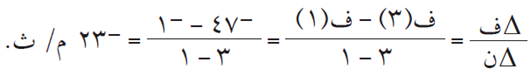
2. السرعة اللحظية = مشتقة المسافة بالنسبة للزمن، أي أن:

ع (ن) = ف^/(ن) = ٣ ن^٢ – ١٨ ن

يعكس الجسم اتجاه حركته في اللحظة التي تتغير فيها إشارة ع (من موجب إلى سالب أو العكس)، وتكون السرعة اللحظية عندها تساوي صفر، ع(ن) = صفر، أي عندما يكون:

٣ ن^٢ – ١٨ ن = صفر أي أن: 3 ن (ن- 6) = صفر، ومنها ن = صفر أو ن = 6.

أي أنه يعكس الجسم اتجاه حركته بعد 6 ثوانٍ من بدء الحركة.

ويكون التسارع يساوي مشتقة السرعة كما يلي:

التسارع ت(ن) = ع^/(ن) = ف^//(ن) = ٦ن – ١٨

وبالتعويض عن ن = 6، نحصل على:

ت(6) = ٦ × ٦ – ١٨ = ١٨ متر/ثانية².

مثال (7) #

قُذف جسم رأسيًا إلى أعلى من نقطة على سطح الأرض، بحيث يتحدد بُعده عن سطح الأرض بالعلاقة ف(ن) = ٢٠ ن – ٥ ن^٢، حيث ف: ارتفاع الجسم بالأمتار، ن: الزمن بالثواني، جد:

1. أقصى ارتفاع يصل إليه الجسم.
2. سرعة الجسم وهو على ارتفاع 15 متر من سطح الأرض.
3. المسافة التي يقطعها الجسم خلال الثواني الأربعة الأولى.

الحل:

المغطيات لدينا: ف(ن) = ٢٠ ن – ٥ ن^٢

1. عندما يصل الجسم إلى أقصى ارتفاع تكون سرعته حينها مساوية صفر، ع(ن) = صفر.

أي أنه بأخذ مشتقة المسافة ف^/(ن) = ع(ن) = ٢٠ – ١٠ ن = صفر، ومنها ن = ٢ ثانية.

أي أن الجسم يصل إلى أقصى ارتفاع بعد ثانيتين، ويكون هذا الارتفاع هو المسافة التي قطعها الجسم خلال ثانيتين، ويتم حسابها بالتعويض عن ن = 2 في معادلة المسافة كما يلي:

أقصى ارتفاع = ف (2) = ٢٠ × 2 – ٥ × 4 = ٢٠ متر.

• عندما يكون الجسم على ارتفاع 15 متر من سطح الأرض، فإن ف(ن) = ١٥، وبالتعويض عن ذلك في معادلة المسافة:

ف(ن) = ٢٠ ن – ٥ ن^٢ = ١٥، أي أن:

٥ ن ^٢ – ٢٠ ن + ١٥ = صفر، ومنها يكون:

)ن – ١) × (ن – ٣) = صفر، ومنها يكون: ن = ١، ن = ٣.

أي أن الجسم يكون على ارتفاع ١٥ متر في اللحظة التي تكون فيها: ن = ١، ن = ٣. وتفسير ذلك أن الجسم يكون عند هذا الارتفاع في حالتين أثناء الصعود وأثناء الهبوط.

ويمكن حساب السرعة اللحظية للجسم في الحالتين كما يلي:

السرعة اللحظية ع (ن) = مشتقة المسافة بالنسبة للزمن = ف^/(ن) = 20 – 10 ن

عندما ن = ١ تكون السرعة ع(١) = ٢٠ – ١٠×1 = ١٠ متر/ثانية، عندما يكون الجسم صاعدًا.

عندما ن = ٣ تكون السرعة ع(3) = ٢٠ – ١٠×3 = – ١٠ متر/ثانية، والإشارة السالبة للسرعة هنا تعني أن اتجاه الحركة هو عكس اتجاه الحركة الأصلي الصاعد، أي أن الجسم يكون هابطًا.

• عندما تكون ن = ٤ ثانية يكون الجسم على ارتفاع:

ف (4) = ٢٠ × 4 – ٥ × 16  = صفر.

وهذا يعني أن الجسم عندها يكون قد وصل إلى سطح الأرض. وبالتالي تكون المسافة المقطوعة عندها تساوي ضعف مسافة أقصى ارتفاع وصل إليه الجسم، أي أن ف = ٢ × أقصى ارتفاع = 2 × 20 = ٤٠ متر. وهي نفس المسافة المقطوعة بعد 4 ثواني أي = ف(4).

مثال (8) #

قُذف جسم رأسيًا إلى أعلى من قمة برج بحيث إن ارتفاعه عن البرج بالأمتار بعد ن ثانية يُعطى بالعلاقة ف(ن) = 30 ن – ٥ ن ^٢، جد:

1. ارتفاع البرج علمًا بأن أقصى ارتفاع للجسم عن سطح الأرض = ١٨٠ متر.
2.  سرعة ارتطام الجسم بسطح الأرض.
3. المسافة الكلية المقطوعة خلال الثواني السبعة الأولى.

الحل

1. عند أقصى ارتفاع عن قمة البرج تكون ع(ن) = صفر

ع(ن) = ف^/(ن) = ٣٠ – ١٠ ن = صفر، ومنها ن = 3.

أقصى ارتفاع عن قمة البرج = ف(3) = 90 – 45 = ٤٥ متر

لكن أقصى ارتفاع عن سطح الأرض = ١٨٠ متر، ارتفاع البرج الفرق = ١٨٠ – ٤٥ = ١٣٥ متر.

يرتطم الجسم بالأرض عندما تكون ف(ن) = – ١٣٥ متر (حيث يكون وكأنه قد غاص تحت مستوى سطح البرج الذي يكون هو منطقة الارتفاع صفر عندما يعود إلى نقطة الانطلاق).

بحل المعادلة ينتج أن ن = 9 ومنها السرعة ع = ٣٠ – ٩ × ١٠ = – ٦٠ م/ ث

عندما ن = 7 تكون الإزاحة = – 35 أي أن المسافة المقطوعة 125 لأنها تساوي = صعود 45 متر + هبوط 45 متر + غوص 35 متر تحت سطح أعلى البرج = 125 متر.

حلول تمارين الكتاب على درس تطبيقات هندسية وفيزيائية #

السؤال الأول #

جد النقطة أو النقط على منحنى الاقتران ق(س) س^٢ – ٢ س + ١ التي يكون عندها المماس للمنحنى عموديًا على المستقيم س + ٢ ص – ٤ = صفر.

الحل

ميل المستقيم = -1/2

ميل المماس = 2 (لأنه عمودي عليه فهو يساوي -1/الميل)

ميل المنحنى = ميل المماس ومن ذلك نستنتج أن المشتقة 2 س – 2 = 2، ومنها س = 2.

فتكون نقطة التماس هي (2، 1).

السؤال الثاني #

جد معادلة المماس لمنحنى الاقتران ق(س) = ٣ – ظا^٢س عندما س = π/4.

الحل

ميل المماس = المشتقة ق^/(π/4) = – ظا (π/4) قا² (π/4) = – 4

ق(π/4) = ٣ – ظا^٢(π/4) = 3 – 1 = 2 ومنها تكون نقطة التماس هي (π/4، 2).

معادلة المماس هي:

س – 2 = – 4 × (س – π/4) ومنها ص = – 4 س + π +  2

السؤال الثالث #

إذا كان المماس لمنحنى الاقتران ق(س) = لو _ه س/2 عندما س = 2 يقطع محور السينات والصادات في النقطتين ب، جـ على الترتيب. جد مساحة المثلث م ب ج ، حيث م نقطة الأصل.

الحل

المشتقة ق^/(س) = 1/س

ميل المماس = ق^/(2) = 1/2

ق(2) = صفر

معادلة المماس هي:

ص – صفر = 1/2 (س – 2) ومنها ص = 1/2 س – 1

المماس يقطع محور السينات في النقطة ب (2، صفر) والصادات في النقطة جـ (صفر، -1)

مساحة المثلث م ب جـ = 1/2 × القاعدة × الارتفاع = 1/2 × 2 × 1 = 1 وجدة مساحة.

السؤال الرابع #

إذا كان المستقيم س = أ – ٦ ص يمس منحنى الاقتران ق(س) = 3 س / (س – 2)، س لا تساوي 2، جد قيمة أ.

الجل

ميل المماس = – 1 / 6

المشتقة ق^/(س) = – 6 / (س – 2)²

ميل المماس = المشتقة ق^/(س) = – 1 / 6 = – 6 / (س – 2)²

وبحل المعادلة ينتج أن:

س = 8 أو س = – 4

عندما س = 8 ، ص = 4 ، أ = 32

عندما س = – 4 ، ص = 2 ، أ = 8

السؤال الخامس #

قذف جسم رأسيًا إلى أعلى وَفق العلاقة ف = ٤٠ ن – ٥ ن^٢، حيث ف ارتفاعه بالأمتار، ن بالثواني. جد سرعة الجسم عندما تكون المسافة الكلية المقطوعة هي 100 متر.

الحل

يصل الجسم إلى أقصى ارتفاع عندما تكون السرعة = صفر، أي أن:

ع(ن) = المشتقة ف^/(ن) = 40 – 10 ن = صفر ومنها ن = 4.

وتكون المسافة المقطوعة عندها = ف(4) = 160 – 80 = 80 متر.

وعندما تكون المسافة الكلية المقطوعة = 100 متر وهي تساوي مسافة أقصى ارتفاع(80 مر) + 20 متر

أي أنه يكون في طريقه بالنزول وعلى ارتفاع قدره 60 متر من سطح الأرض. أي أنه يكون عندها:

40 ن – 5 ن² = 60 منها ن = 2 أو 6 ثواني، ويتم إهمال ن = 2 لأنها تكون أثناء الصعود.

وتكون سرعة الجسم في اللحظة المطلوبة هي:

ع(ن) = ف^/(ن) = 40 – 10 × 6 = – 20 متر/ثانية. (والإشارة السالبة تعني أن السرعة ياتجاه النزول).

السؤال السادس #

من نقطة على سطح الأرض قُذف جسم رأسيًا إلى أعلى، وكان ارتفاعه ف بالأمتار بعد ن من الثواني يُعطى بالعلاقة ف = ٣٠ ن – ٥ ن 2.

جد:

• أقصى ارتفاع يصله الجسم.
• سرعة الجسم وهو نازل عندما يكون على مستوى سطح العمارة التي ترتفع ٤٠ متر.

الحل

أقصى ارتفاع يصله الجسم هو عندما تكون السرعة = صفر.

ع(ن) = ف^/(ن) = 30 – 10 ن = صقر، ومنها ن = 3 ث.

أقصى ارتفاع = ف(3) = 45 متر.

وعندما يكون الجسم على مستوى سطح العمارة تكون الإزاحة = 40 متر، أي يكون:

30 ن – 5 ن² = 40

ن = 2 أو ن = 4 (إهمال ن = 2 لأنها أثناء الصعود).

السرعة في تلك اللحظة تكون = 30 – 10 × 4 = –  10 متر/ثانية (اتجاه الهبوط).