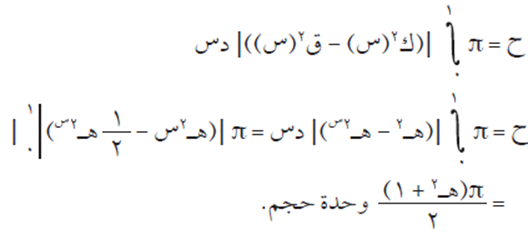تطبيقات التكامل المحدود – أولًا: المساحة
الحالة الأولى: مساحة منطقة محصورة بين منحنى اقتران ومحور السينات في الفترة [أ، ب]:
نظرية (1)
إذا كان ق(س) اقترانًا قابلًا للتكامل في [أ، ب] فإن مساحة المنطقة المحصورة بين منحنى الاقتران ق(س) ومحور السينات في [أ، ب] تُعطى بالعلاقة:
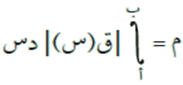
مثال (1)
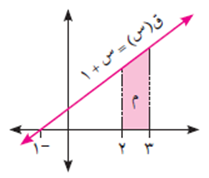
احسب مساحة المنطقة المحصورة بين منحنى الاقتران ق(س) = س + ١ ومحور السينات والمستقيمين س = 2 ، س = 3.
الحل
نجد نقاط تقاطع منحنى الاقتران ق(س) مع محور السينات، وذلك بوضع س + 1 = صفر ومنها س = – 1 لا تنتمي للفترة [2، 3]>
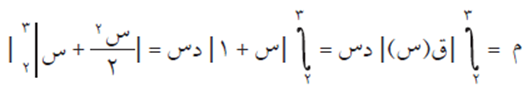
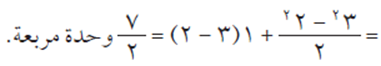
الحالة الثانية: مساحة المنطقة المحصورة بين منحنيين، أو أكثر
نظرية (2)
إذا كان ق(س)، ه(س) اقترانين قابلين للتكامل في [أ، ب] فإن مساحة المنطقة المحصورة بين منحنيي ق(س)، ه(س) في [أ، ب] تُعطى بالعلاقة:
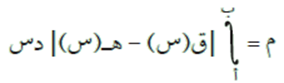
مثال (2)
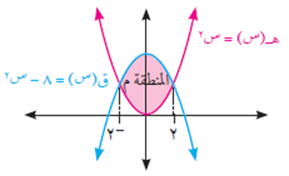
جد مساحة المنطقة المحصورة بين منحنيي الاقترانين ق(س) = ٨ – س٢، ه(س) = س2
الحل
نجد نقاط التقاطع بين منحنيي الاقترانين ق(س)، ه(س) بوضع ق(س) = ه(س) فتكون ق(س) – ه(س) = صفر. أي أن:
٨ – ٢ س٢ = صفر ومنها س = ± 2
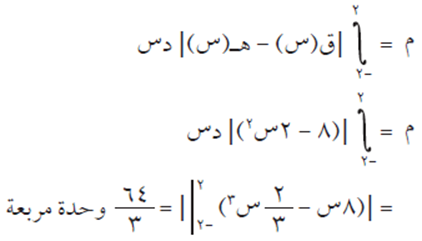
تطبيقات التكامل المحدود – ثانيًا: الحجوم الدورانية
نظرية
إذا كان ق(س): [أ، ب] ⟵ ح، وكان الاقتران ق2(س) قابلًا للتكامل على [أ، ب]، فإن حجم الجسم الناتج من دوران المنطقة المحصورة بين منحنى الاقتران ق(س) ومحور السينات والمستقيمين س = أ، س = ب دورة كاملة حول محور السينات يعطى بالقاعدة:
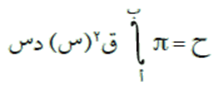
مثال (3)
جد حجم الجسم الناتج من دوران المنطقة المحصورة بين منحنى الاقتران ق(س) = 2 س ومحور السينات والمستقيمين س = ١، س = ٣ دورة كاملة حول محور السينات.
الحل
بتطبيق النظرية:
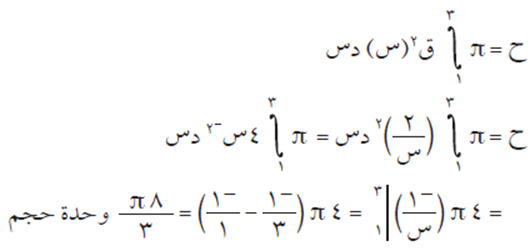
نظرية
إذا كان ق2(س)، ه2(س) اقترانين قابلين للتكامل في [أ، ب[ وكان منحنى الاقتران ه(س)، ومنحنى الاقتران ق(س) يقعان على جهة واحدة من محور السينات، فإن حجم الجسم الناتج من دوران المنطقة المحصورة بينهما دورة كاملة حول محور السينات هو:
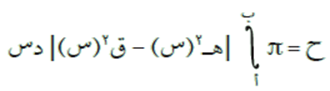
مثال (4)
جد حجم الجسم الناتج من دوران المنطقة المحدودة بمنحنيي الاقترانين ق(س) = هس، ك(س) = ه ومحور الصادات دورة كاملة حول محور السينات.
الحل
نجد نقاط التقاطع بين منحنيي الاقترانين ق(س)، ك(س(.
بوضع ق(س) = ك(س) ينتج أن: هس = ه ومنها س = ١.
ثم بتطبيق النظرية: