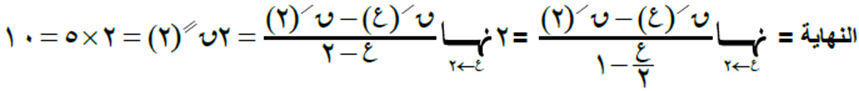قاعدة لوبيتال ومشتقة الاقتران الأسّي واللوغاريتمي
أولًا: قاعدة لوبيتال L’Hôpital’s Rule
إذا كان ق(س)، هـ(س) اقترانين قابلين للاشتقاق عند النقطة س = أ، وكانت ل ϶ ح، وكانت:
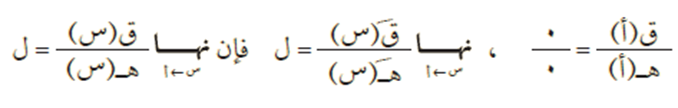
مثال (1)
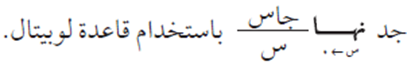
الحل
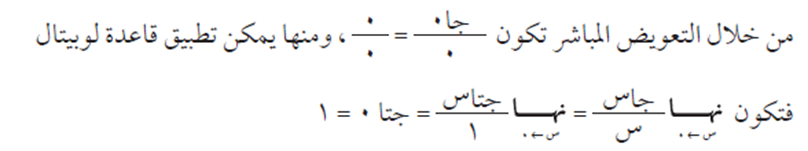
نشاط

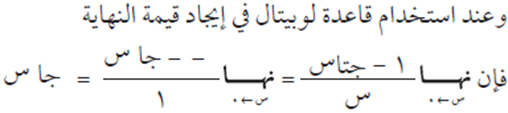
مثال (2)
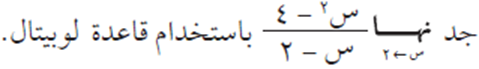
الحل

ملاحظة هامة

مثال (3)

مثال (4)
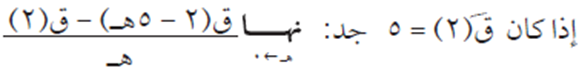
الحل
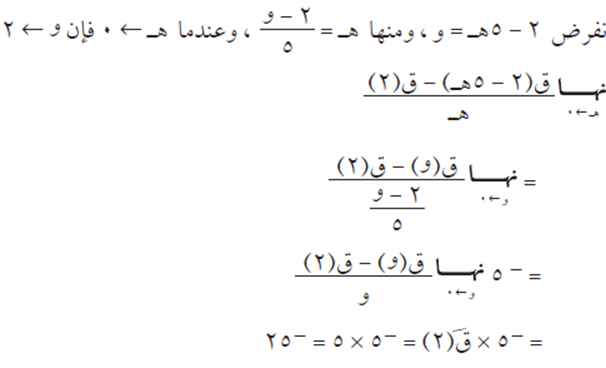
ثانيًا: مشتقة الاقتران الأسّي واللوغاريتمي
تعلمت سابقًا الاقتران الأسّي الذي يُكتب على الصورة ق(س) = أ س، حيث أ ≠ ١، أ < صفر.
كما تعلمت الاقتران اللوغاريتمي الذي يُكتب على الصورة:
ل(س)= لو أ س
حيث س > صفر، أ ≠ ١، أ > صفر.
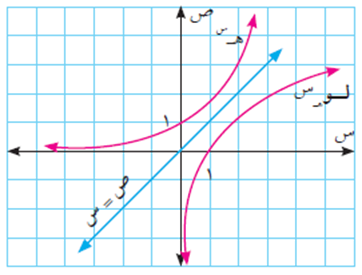
وسوف نقتصر دراستنا على الاقتران الأسّي الطبيعي ق(س) = ه س، والاقتران اللوغاريتمي الطبيعي:
ق(س) = لو ه س
حيث ه تسمى العدد النيبيري e.
تعريف العدد النيبيري

وفيما يلي بعض خصائص الاقترانين:
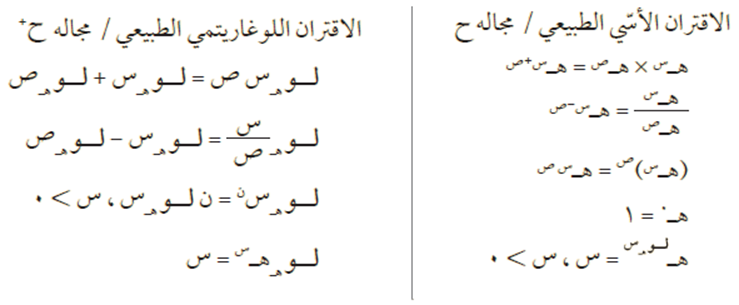
قاعدة (1)
إذا كان ص = ه س، فإن لــــــوه ص = س، ص < صفر.
قاعدة (2)
إذا كان ق(س) = ه س فإن ق/(س) = ه س
مثال (5)
إذا كان ق(س) = س٣ ه س + قتا س فجد ق/(س).
الحل
تذكير: مشتقة س٣ ه س = (الأول × مشتقة الثاني + الثاني × مشتقة الأول)
إذن: المشتقة ق/(س) = (س٣ ه س + ٣ س٢ هس ) – قتاس ظتاس
قاعدة (3)
إذا كان ق(س) = لـــــو ه س، س > صفر ، فإن ق/(س) = ١ / س.
مثال (6)
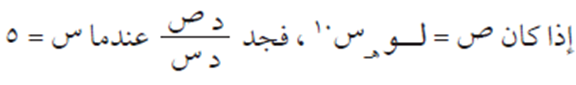
الحل
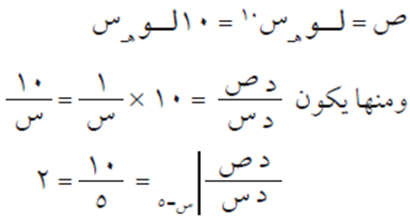
مثال (7)

الحل

مثال (8)

الحل
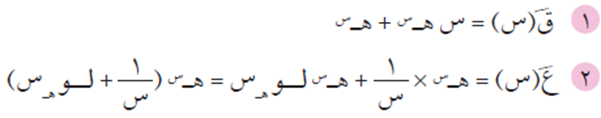
حلول تمارين الكتاب على درس قاعدة لوبيتال ومشتقة الاقتران الأسي واللوغاريتمي
السؤال الأول

الحل

السؤال الثاني
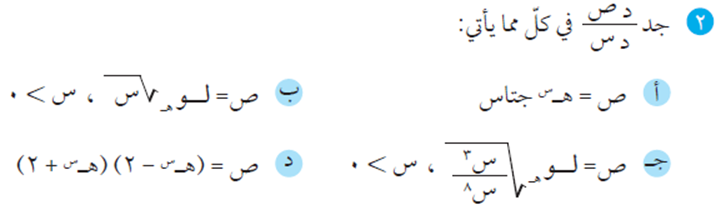
الحل
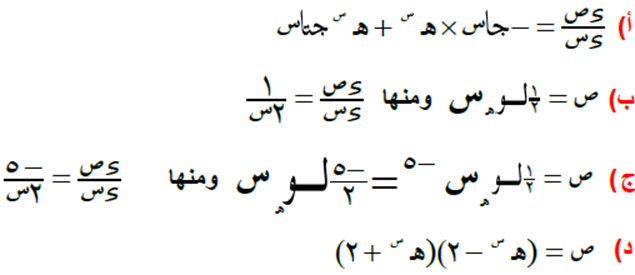
السؤال الثالث
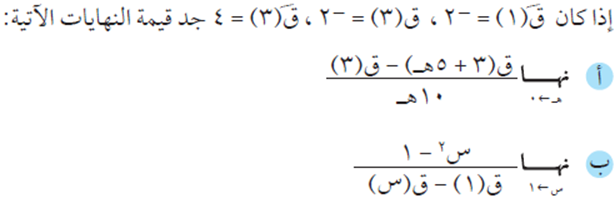
الحل
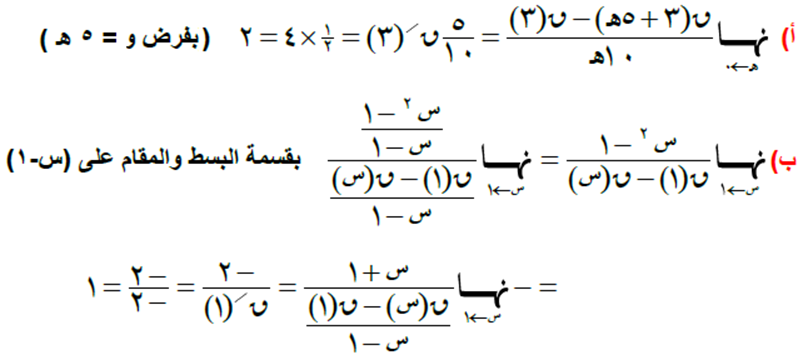
السؤال الرابع
إذا كانت ص = س٢ + هس + ١، فجد قيمة/ قيم س التي تجعل ص/ = ص
الحل
المطلوب هو إيجاد قيمة أو قيم س التي تجعل ص/ = ص
ولكن ص/ = 2 س هس
إذن المطلوب إيجاد قيمة أو قيم س التي تجعل:
2 س هس = س٢ + هس + ١
وبالتبسيط ينتج:
س٢ – 2 س + ١ = صفر
(س – 1)2 = صفر
وبحل المعادلة ينتج أن س = 1.
السؤال الخامس
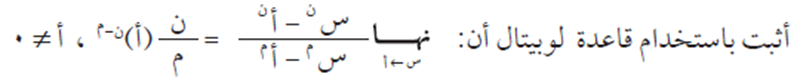
الحل
بما أنه بالتعويض المباشر تنتج القيمة ضفر/صفر، إذن نقوم بتطبيق قاعدة لوبيتال:
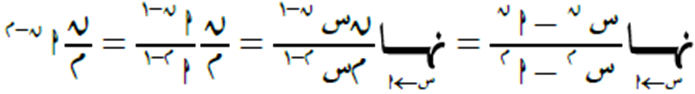
السؤال السادس

الحل
بما أنه بالتعويض المباشر تنتج القيمة ضفر/صفر، إذن نقوم بتطبيق قاعدة لوبيتال:
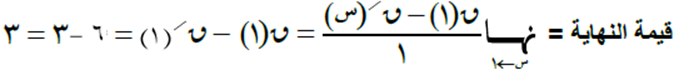
السؤال السابع
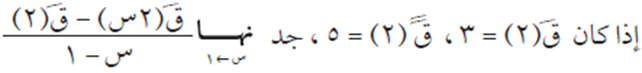
الحل
بهدف التبسيط، نفرض أن 2 س = ع ومنها يكون س = ع/2
وعندما س تؤول إلى 1 فإن ع س تؤول إلى 2، وبالتعويض في المطلوب إيجاده، فتكون النهاية المطلوب إيجادها هي: