1. نظرية رول ونظرية القيمة المتوسطة
أولًا: نظرية رول
إذا كان ق (س) اقتران متصل في الفترة [أ ، ب]، وقابلاً للاشتقاق في ]أ ، ب[، وكان ق(أ) = ق(ب) فإنه يوجد عدد حقيقي واحد على الأقل جـ ϶ ]أ ، ب[ بحيث يكون عنده قَ(جـ) = صفر.
مثال (1)
بيّن أن الاقتران ق(س) = س 2 – س – 6 يحقق شروط نظرية رول في الفترة [0، 1]. ثم جد قيمة، أو قيم جـ التي تعينها النظرية.
الحل
نبحث في تحقق شروط نظرية رول على الإقتران ق(س) في الفترة [0، 1]:
ق(س) متصل في الفترة [0، 1]، وقابل للاشتقاق في الفترة ]0، 1[ لأنه كثير حدود.
ق(0) = – ٦، ق(1) = – ٦، ومنها ق(0) = ق(1)
وبالتالي تحققت شروط نظرية رول.
إذن يوجد على الأقل عدد جـ ϶ ]0، 1[ بحيث يكون ق/(ج) = صفر.
ثم نجد قيمة/ قيم جـ التي تعينها النظرية بالتعويض المباشر كما يلي:
ق/(س) = 2 س – ١ ومنها ق/(جـ) = 2 جـ – ١ = صفر
إذن جـ = 1/2 (وهي قيمة تنتمي للفترة ]0، 1[)
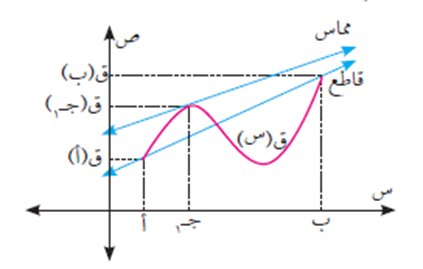
ثانيًا: نظرية القيمة المتوسطة
إذا كان ق(س) اقتران متصل في الفترة [أ ، ب]، وقابل للاشتقاق في الفترة ]أ ، ب[، وكان ق(أ) = ق(ب) فإنه يوجد عدد حقيقي واحد على الأقل جـ ϶ ]أ ، ب[، بحيث أن:
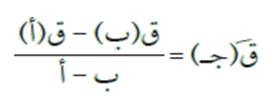
مثال (2)
بيّن أن الاقتران ق(س) = س 3 + ١ يحقق شروط نظرية القيمة المتوسطة في الفترة [-2، 1]، ثم جد قيمة/ قيم جـ التي تحددها النظرية.
الحل
نبحث أولًا في تحقق شروط نظرية القيمة المتوسطة على الاقتران ق(س) في الفترة [-2، 1]:
الاقتران ق(س) متصل في الفترة [-2، 1]، وقابل للاشتقاق في الفترة ]-2، 1[، لأنه كثير حدود.
إذن تحققت شروط نظرية القيمة المتوسطة على الاقتران ق(س) في الفترة [-2، 1]، وبالتالي قإنه يوجد على الأقل عدد جـ ϶ ]-2 ، 1[، بحيث يكون:
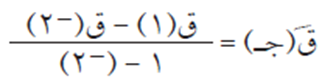
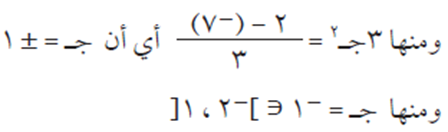
لأن +1 لا تنتمي للفترة ]-2 ، 1[.





