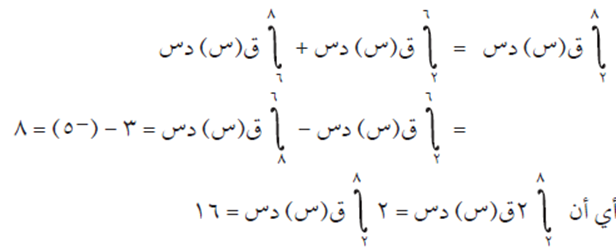بعض خصائص التكامل المحدود
للتكامل المحدود خصائص مهمة تسهل حساب قيمته، ومنها:
إذا كان ق(س)، ه(س) اقترانين قابلين للتكامل على [أ ، ب] فإن:

مثال (1)
جد قيمة ما يلي:
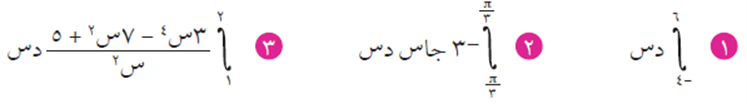
الحل
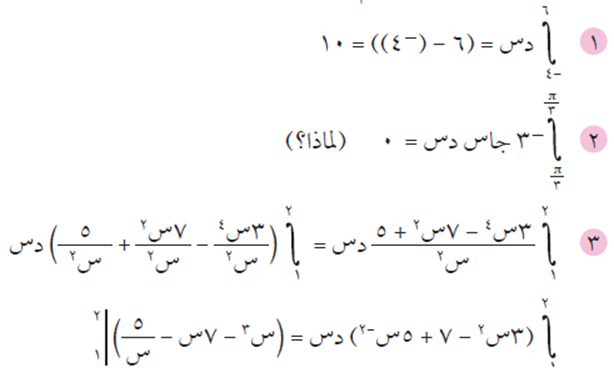
ثم نقوم بالتعويض عن قيمة س بالقيم 1، 2 لإيجاد الناتج.
نظرية
إذا كان ق(س) اقترانًا قابلًا للتكامل في الفترة [أ ، ب]، وكان ق(س) ≤ صفر لكل س ϶ [أ ، ب]، فإن:
مثال (2)
بدون حساب التكامل، بيّن أن:
الحل
نبحث في إشارة المقدار 3 س / (س2 + 4) في الفترة [صفر ، 5].
وبما أن 3 س ≥ صفر ، لكل س ϶ [صفر، 5].
وكذلك س٢ + ٤ ≥ ٤ ≥ صفر ، لكل س ϶ [صفر، ٥].
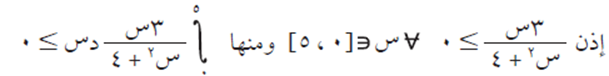
خاصية المقارنة
إذا كان ق(س)، ه(س) اقترانين قابلين للتكامل في الفترة [أ ، ب]، وكان ق(س) ≥ ه(س) لكل س ϶ [أ ، ب]، فإن:
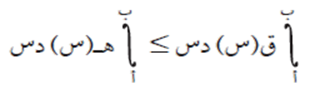
مثال (3)
بدون إجراء التكامل، بيّن أن:
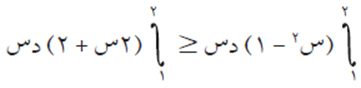
الحل
نفرض أن ق(س) = س٢ – ١ – (٢ س + ٢) = س٢ – ٢ س – ٣
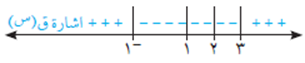
نبحث في إشارة الاقتران ق(س) = س٢ – ٢ س – ٣
فنلاحظ أن ق(س) ≤ صفر في الفترة [1، ٢[، أي أن س٢ – ٢ س – ٣ ≤ صفر. (انظر الشكل أدناه).
أي أن:
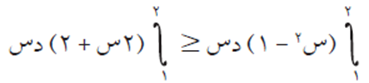
خاصية الإضافة
إذا كان ق(س) اقترانًا قابلًا للتكامل في الفترة ف ⊇ ح وكان أ، ب، ج أي ثلاثة أعداد تنتمي للفترة ف فإن:
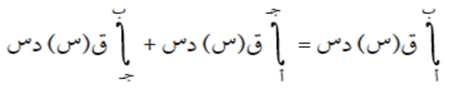
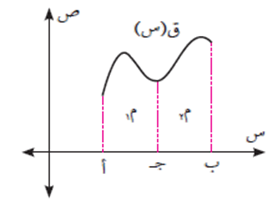
مثال (4)
عبّر بتكامل واحد عما يلي:
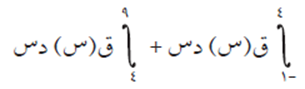
الحل
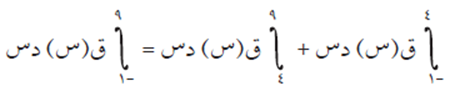
مثال (5)
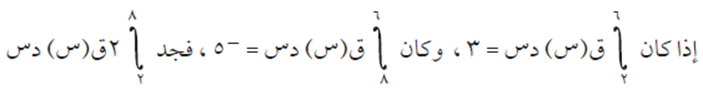
الحل