العلاقة بين التفاضل والتكامل
تعريف
إذا كان م(س) هو أحد الاقترانات الأصلية للاقتران المتصل ق(س) في الفترة [أ ، ب]، فإن المقدار م(ب) – م(أ) يساوي التكامل المحدود للاقتران ق(س) في الفترة [أ ، ب] ونرمز له بالرمز:

النظرية الأساسية للتفاضل والتكامل
- إذا كان الاقتران ق(س) متصلًا في الفترة [أ ، ب]، وكان م(س) اقترانًا أصليًا للاقتران ق(س) فإن:
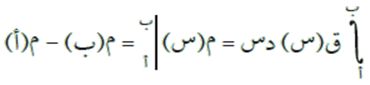
- إذا كان الاقتران ق(س) قابلًا للتكامل في الفترة [أ ، ب]، فإن:
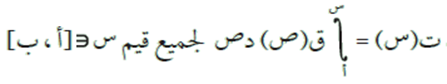
ويسمى ت(س) الاقتران المكامل للاقتران ق(س).
وإذا كان ق(س) اقترانًا متصلًا، فإن ت/(س) = ق(س) لكل س ϶ [أ ، ب].
مثال (1)
جد قيمة:
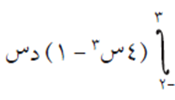
الحل
ق(س) = ٤ س٣ – ١ متصل على ح، م(س) = س٤ – س اقتران أصلي للاقتران ق(س)، إذن:
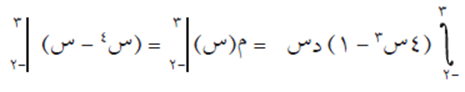
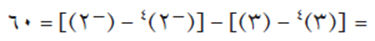
نظرية
إذا كان ت(س) هو الاقتران المكامل للاقتران ق(س) المعرف في الفترة [أ ، ب]، فإن:
- ت(س) اقتران متصل دائمًا في الفترة [أ ، ب].
- ت(أ) = صفر.





