2. العمليات على المصفوفات

2. العمليات على المصفوفات #

أولاً: جمع المصفوفات #

إذا كانت أ ، ب مصفوفتين من الرتبة م × ن، فإن حاصل جمعهما هو المصفوفة ج = أ + ب، وهي مصفوفة من الرتبة م × ن بحيث تكون مدخلاتها ناتجة من جمع المدخلات المتناظرة في كل من المصفوفتين أ، ب. أي أن:

ج _{ي ه} = أ _{ي ه} + ب _{ي ه}

مثال (1) #

إذا كانت:

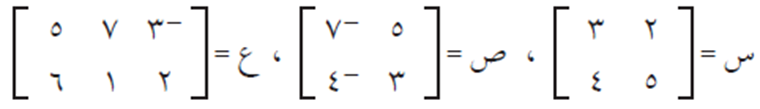
جد ناتج ما يلي إن أمكن:

• س + ص
• ص + س
• ص + ع

الحل:

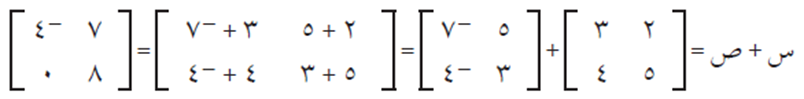
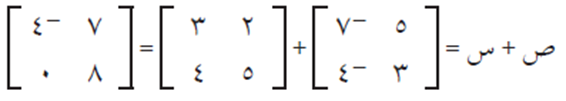
لاحظ أن: س + ص = ص + س، أي أن عملية جمع المصفوفات هي عملية إبدالية.

أما بالنسبة لـ ص + ع فهي عملية غير معرّفة، لأن رتبة ص ≠ رتبة ع.

ثانيًا: ضرب المصفوفة بعددٍ حقيقيٍ #

إذا كانت أ مصفوفةً من الرتبة م × ن، وكان ك عددًا حقيقيًا، فإن حاصل ضرب العدد ك في المصفوفة أ ك ×  أ = المصفوفة ج، حيث ج مصفوفة من الرتبة م × ن، وتكون مدخلاتها كما يلي:

ج _{ي ه} = ك × أ _{ي ه} لجميع قيم ي، ه

مثال (2) #

إذا  كانت:

فجد: ٢ أ ، – أ ، أ + ( – أ )

الحل:

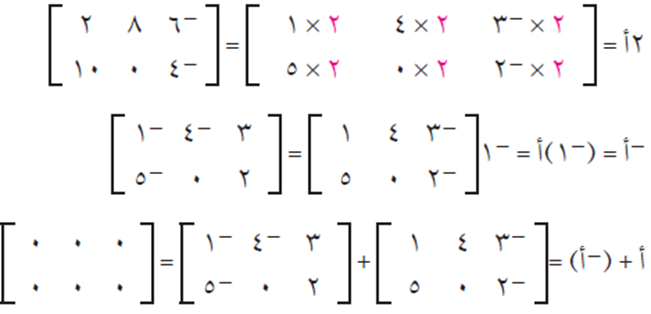
لاحظ أن ناتج جمع أ + ( – أ ) هو المصفوفة الصفرية، (و)، هي المصفوفة التي جميع مدخلاتها أصفار، وذلك يعني أن المصفوفة ( – أ ) هي النظير الجمعي للمصفوفة أ، وحاصل جمعهما هو المصفوفة الصفرية.

ثالثاً: طرح المصفوفات #

إذا كانت أ، ب مصفوفتين من نفس الرتبة م × ن، فإن حاصل الطرح أ – ب = أ + (- ب(

مثال (3)

إذا كان:

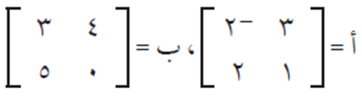
فجد المصفوفة ب – أ

الحل:

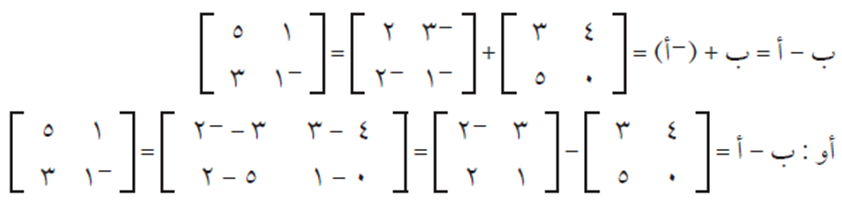
لاحظ أن مدخلات ب – أ تنتج من طرح مدخلات المصفوفة أ من المدخلات المناظرة لها في المصفوفة ب، أي أن:

ب – أ  _{ي ه} = ب _{ي ه} – أ _{ي ه}

خصائص جمع المصفوفات وضربها بعددٍ حقيقيٍ #

إذا كانت ( أ ، ب ، ج ، و ) مصفوفات من نفس الرتبة، ك ∋ ح فإن:

1. أ + ب = ب + أ … (الخاصيّة التبديلية أو الإبدال)
2. ( أ + ب ) + ج = أ + ( ب + ج ) … (الخاصيّة التجميعية)
3. أ + و = و + أ = أ … (المصفوفة الصّفّرية المحايدة لعملية جمع المصفوفات)
4. أ + ( – أ ) = ( – أ ) + أ = و … (النظير الجمعي وهو المصفوفة الصفرية)
5. ك ( أ + ب ) = ك أ + ك ب … (خاصية توزيع الضرب بعدد حقيقي على جمع المصفوفات)

رابعًا: ضرب المصفوفات #

إذا كانت أ مصفوفة من الرتبة م × ن، ب مصفوفة من الرتبة ن × ل، فإن حاصل الضرب المصفوفتين أ . ب يساوي المصفوفة ج، حيث ج مصفوفة من الرتبة م × ل، وتكون مدخلات المصفوفة ج على النحو التالي:

ج _{ي ه} = أ _{ي 1} ×  ب _{1 ه} + أ _{ي ٢} × ب _{2 ه} + أ  _{ي 3} × ب _{3 ه} ……… + أ _{ي ن} × ب _{ن ه}

مثال (4) #

يعمل ثلاثة خيّاطين في مشغلٍ للخياطة، ينتج ثلاثة أنواع من الألبسة، قميص، بنطال، بلوزة. فإذا كانت أجرة خياطة القميص 5 دنانير، وأجرة خياطة البنطال 6 دنانير، وأجرة خياطة البلوزة 3 دنانير. وفي أحد الأيام كان إنتاجهم كما في الجدول التالي:

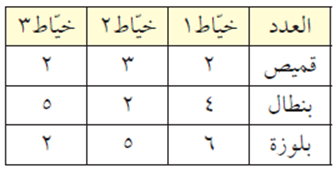
فما هي الأجرة التي حصل عليها كل خياط في ذلك اليوم؟

الحل:

لحساب أجرة الخيّاط الأول مثلاً، فإننا نجري العمليات الآتية:

2 × 5 + 4 × 6 + 6 × 3 = 52 دينارًا.

ولكن باستخدام المصفوفات يمكن حساب أجرة كل خيّاط، بحيث نقوم بتكوين مصفوفتين: الأولى مصفوفة أجرة خياطة القطعة الواحدة من كل نوع، وهي كما يلي:

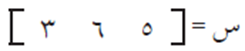
والمصفوفة الثانية هي مصفوفة كميات إنتاج الخيّاطين ذلك اليوم والموضحة في الجدول، وهي كما يلي:

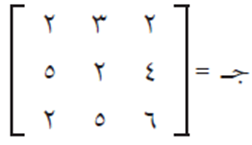
وعليه فإن أجرة كل خيّاط يتم استخراجها من ناتج حاصل ضرب المصفوفتين س × ج كما يلي:

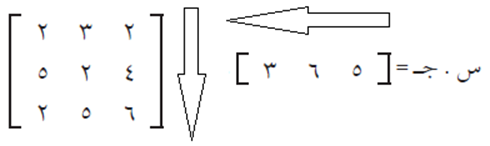
وبتطبيق عملية الضرب ينتج:

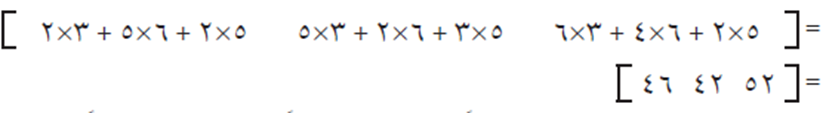
وتكون أجرة الخيّاط الأول 52 دينارًا، والثاني 42 دينارًا، والثالث 46 دينارًا.

خصائص عملية الضرب على المصفوفات #

إذا كانت أ ، ب، ج مصفوفات حيث أن عمليتي الضرب والجمع معرفتان، م المصفوفة المحايدة، ك ∋ ح فإن:

1. ( أ . ب ) . ج = أ . ( ب . ج ) …. الخاصيّة التجميعيّة.
2. أ . ( ب + ج ) = ( أ . ب ) +  ( أ . ج ) …. توزيع الضرب على الجمع من اليمين.
3. ( أ + ب ) . ج =  ( أ . ج ) + ( ب . ج ) …. توزيع الضرب على الجمع من اليسار.
4. أ . م = م . أ = أ …. المصفوفة المحايدة م وهي العنصر المحايد لعملية ضرب المصفوفات.
5. ك ( أ . ب ) = ( ك أ ) . ب = أ . ( ك ب )

مثال (5) #

إذا كانت:

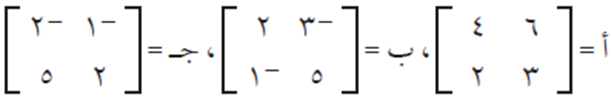
فجد أ . ب ، أ . ج

الحل

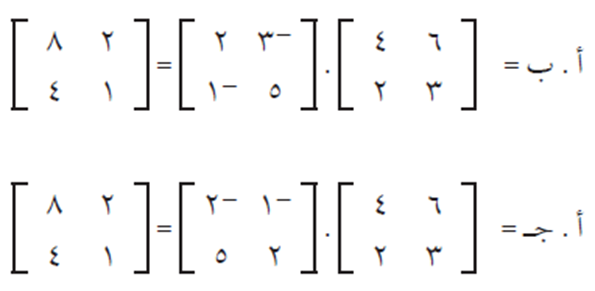
نلاحظ من النتيجة أن حاصل الضرب أ . ب يساوي حاصل الضرب أ . ج، ولكن ب ≠ ج. وهذا يعني أن عملية ضرب المصفوفات تختلف بشكل كبير عن عملية الضرب العادية.