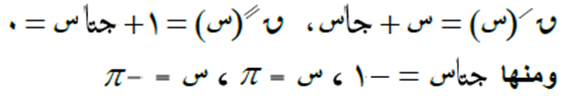مشتقات الاقترانات المثلثية
يمكن تعريف مشتقات الاقترانات المثلثية أو مشتقات الدوال المثلثية من خلال القواعد التالية:
قاعدة (1)
إذا كانت ق(س) = جا س، والزاوية س بالتقدير الدائري، فإن: ق/(س) = جتا س.
مثال (1)
إذا كان ق(س) = س جا س، جد ق/(π/2)
الحل
قَ(س) = 1 × جا س + س جتا س
ق(π/2) = 1 × 1 + 1 × صفر = 1
قاعدة (2)
إذا كانت ق(س) = جتا س، والزاوية س بالتقدير الدائري، فإن: ق/(س) = – جا س.
مثال (2)
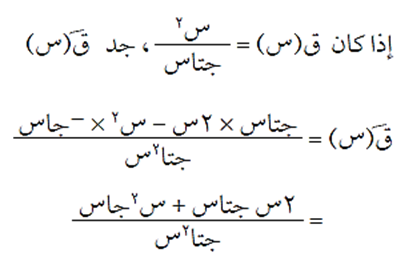
قاعدة (3)
إذا كانت ق(س) = ظا س، فإن: ق/(س) = قا2 س.
إذا كانت ق(س) = ظتا س، فإن: ق/(س) = – قتا2 س.
إذا كانت ق(س) = قا س، فإن: ق/(س) = – قا س ظا س.
إذا كانت ق(س) = قتا س، فإن: ق/(س) = – قتا س ظتا س.
فكر وناقش
تحقق من صحة القواعد السابقة بالتعويض بدلالة جاس، جتاس، ثم باستخدام قواعد الاشتقاق.
يمكن التحقق بتطبيق القواعد وباستخدام خواص الاقترانات المثلثية التي تعلمتها في السنوات السابقة كما يلي:
بما أن ق(س) = ظا س = جاس / جتاس، وبالتالي فإن المشتقة هنا لحاصل قسمة اقترانين، فتكون:
ق/(س) = (جتاس جتاس – جاس × – جاس) / (جتاس)2 = ((جتاس)2 + (جاس)2) / (جتاس)2 = 1/ (جتاس)2 = قا2س.
مثال (3)
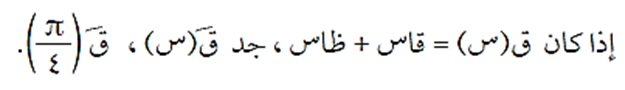
الحل
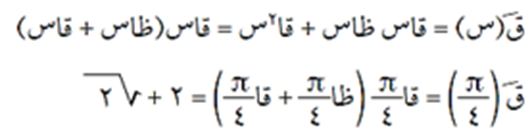
بتطبيق قواعد وخواص الاقترانات المثلثية وعلاقتها ببعضها البعض.
مثال (4)

الحل

حلول تمارين الكتاب على درس مشتقات الاقترانات المثلثية
السؤال الأول

الحل

السؤال الثاني

الحل
بأخذ المشتقة الأولى:
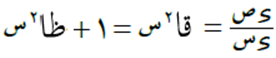
ثم نقوم بأخذ المشتقة الثانية ولكن مع اعتبار أن ظا2س = ظاس × ظاس، لتطبيق قاعدة مشتقة حاصل ضرب اقترانين، وقاعدة مشتقة الاقتران ظاس = قا2س، فنحصل على:
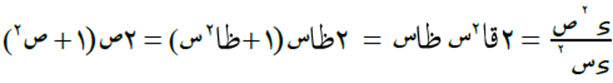
السؤال الثالث
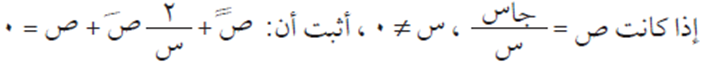
الحل
بأخذ المشتقة الأولى ثم أخذ المشتقة الثانية وتطبيق قواعد الاشتقاق للاقترانات المثلثية ثم مع التبسيط والاختصار نحصل على:

السؤال الرابع

الحل
بأخذ المشتقة الأولى ثم المشتقة الثانية وبتطبيق قواعد اشتقاق الاقترانات المثلثية، نحصل على: