التكامل المحدود
مراجعة قواعد التجميع
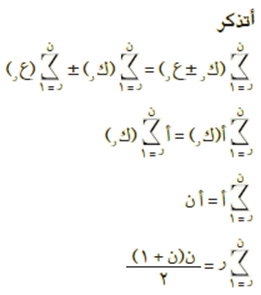
تعريف التكامل المحدود
إذا كان الاقتران ق(س) معرفًا ومحدودًا في الفترة [أ ، ب]، وكانت:
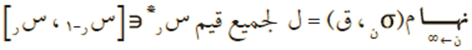
فإن الاقتران ق(س( يكون قابلًا للتكامل في الفترة [أ ، ب]، ويكون:
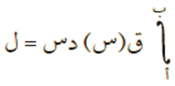
ونسمي أ، ب حدود التكامل.
مثال (1)
إذا كان ق(س) = 5 – 4 س، حيث س ϶ [صفر،3]، وباعتبار س ر * = س ر-1، احسب:

الحل
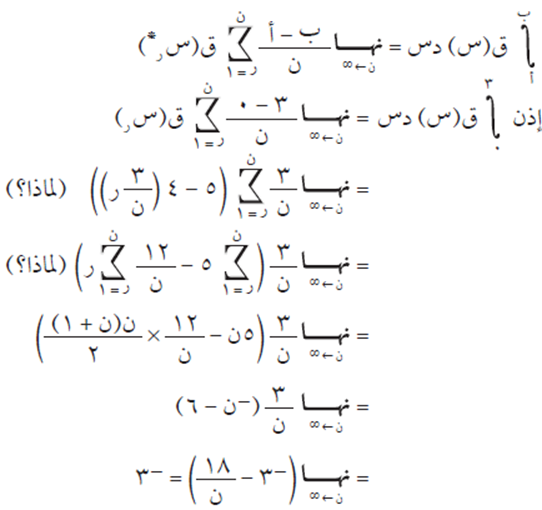
تذكر أن:

قابلية الاقتران ق(س) للتكامل في الفترة [أ ، ب]
نظرية (1)
إذا كان ق(س) اقترانًا متصلًا في الفترة [أ ، ب[، فإنه يكون قابلاً للتكامل في الفترة [أ ، ب].
نظرية (2)
إذا كان الاقتران ق(س) قابلًا للتكامل في الفترة [أ ، ب]، وكان الاقتران ه(س) = ق/(س( لجميع قيم س ϶ [أ ، ب]، عدا عند مجموعة منتهية من قيم س في تلك الفترة، فإن ه(س( يكون قابلًا للتكامل في الفترة [أ ، ب]، ويكون:
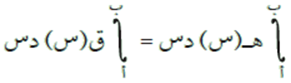
مثال (2)
ابحث في قابلية التكامل للاقتران ق(س) = [1/2 س]، في الفترة [4، 6].
الحل
نعلم أن:
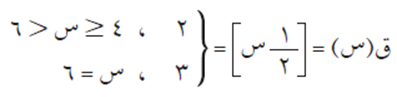
نفرض أن ه(س) = ٢ حيث س ϶ [4، 6]ـ، لاحظ أن ه(س) قابل للتكامل لأنه متصل. وبما أن ه(س) = ق/(س) لجميع قيم س ϶ [4، 6]. ما عدا عند س = 6 فإن الاقتران ق(س) = [1/2 س] يكون قابلًا للتكامل على الفترة [4، 6].





