متوسط تغير الاقتران Rate of Change

متوسط تغير الاقتران Rate of Change

مفهوم الاقتران أو الدالة

الاقتران أو الدالة هو علاقة رياضية تربط بين متغيرين، أحدهما يُطلق عليه اسم المتغير المستقل والآخر يُطلق عليه اسم المتغير التابع. بحيث يتأثر المتغير التابع في كل مرة تتغير فيها قيمة المتغير المستقل.

 وبالمعنى الاصطلاحي فإن مفهوم الاقتران يعني أن المتغير التابع مقترن بالمتغير المستقل ويتبعه ويتغير بتغيره. وكذلك فإن مفهوم الدالة يعني أن المتغير المستقل يدل على المتغير التابع ويساعد في تحديد قيمته في كل مرة يأخذ فيها المتغير المستقل قيمة جديدة.

ومن أمثلة الاقتران في الحياة اليومية، العلاقة بين قيمة فاتورة استهلاك الكهرباء الشهرية (متغير تابع) وكمية الكهرباء التي يتم استهلاكها خلال الشهر (متغير مستقل)، فمثلاً يمكن التعبير عن هذا الاقتران كما يلي:

ص = ق (س)

فإذا افترضنا أن هذه العلاقة محددة بالاقتران التالي:

قيمة فاتورة استهلاك الكهرباء الشهرية = كمية الكهرباء المستهلكة × 0.75

أو بالرموز:

ص = ق (س) = س × 0.75

وباستخدام هذا الاقتران، يمكن معرفة قيمة الفاتورة بمعرفة كمية الكهرباء المستهلكة. فإذا كانت هذه الكمية س = 400 كيلو وات، فإن قيمة الفاتورة ص = 0.75 × 400 = 300 دولار.

وهكذا، سوف تتغير قيمة الفاتورة (ص) في كل مرة تتغير فيها كمية الاستهلاك (س)، وهذا هو تفسير مفهوم الاقتران أو الدالة ص = ق (س).

تعريف متوسط تغير الاقتران

إذا كان ص = ق (س) اقترانًا وتغيرت س من س₁ إلى س₂، وكانت س₁ ≠ س₂ فإن:

التغير في س يساوي س₂ – س₁ ويُرمز له بالرمزΔس ، ويُقرأ دلتا س .

التغير في الاقتران ص = ق (س) يساوي ص₂ – ص₁ أو يساوي ق (س_٢) – ق (س_١)، ويرمز له بالرمزΔص، ويُقرأ دلتا ص.

متوسط التغير في الاقتران ص = ق (س) يساوي ∆ ص / ∆ س

= ص₂ – ص₁ / س₂ – س₁

= ( ق (س₂) – ق (س_١) ) / (س₂ – س₁)

ويمكن كتابته على الصورة ∆ ص / ∆ س = ق (س₁ + ه) – ق (س_١) / ه

حيث ه = ∆ س ≠ صفر (مقدار التغير في س).

ويطلق عليه اقتران متوسط التغير عند س₁.

مثال (1)

إذا كان ص = ق (س) = س ^٣ – ٥ س + ٣، جد:

1. ∆ س عندما تتغير س من – ١ إلى ٢.
2. التغير في ق (س) عندما تتغير س من – ١ إلى ٢.
3. متوسط التغير في ق (س) عندما تتغير س من – 1 إلى 2.

الحل

1. بما أن س₁ = -1، س₂ = 2، فإن ∆س = س₂ – س₁ = 3
2. ∆ص = ق (س₂) – ق (س₁) = ق(2) – ق(-1) = 1 – 7 = -6
3. متوسط التغير = ∆ ص / ∆ س = – 6 / 3 = – 2

المعنى الهندسي لمتوسط التغير

في الشكل المقابل، نفرض أنه يمثل منحنى الاقتران ق (س)، ونفرض أن -النقطتين أ (س₁، ص₁)، ب (س₂، ص₂)، تقعان على المنحنى. فيكون:

التغير في س = ∆س = س₂ – س₁

التغير في ص = ∆ص = ص₂ – ص₁ = ق (س₂) – ق (س₁)

متوسط التغير للاقتران ص = ق(س) = ∆ ص / ∆ س = (ق (س₂) – ق (س₁)) / (س₂ – س₁)

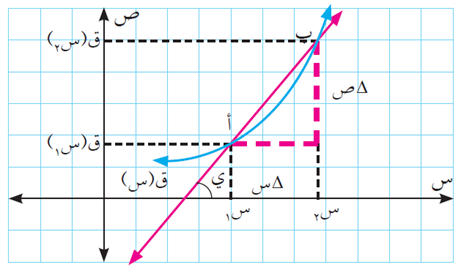
ولكن من الرسم الهندسي، نلاحظ أن ∆ ص / ∆ س = ظا ي (ظل الزاوية ي = ∆ ص / ∆ س)

أي أن ∆ ص / ∆ س = ميل المستقيم المار بالنقطتين أ، ب، والذي يُسمى قاطع للمنحنى ص = ق (س). (ميل أي مستقيم = ظل الزاوية التي يصنعها مع الاتجاه الموجب لمحور السينات = ظا ي).

التعريف الهندسي لمتوسط تغير الاقتران

متوسط التغير للاقتران ق (س) عندما تتغير س من س1 إلى س2 يساوي ميل القاطع المار بالنقطتين (س1، ق (س1))،  و(س2، ق(س2))، ونسمي الزاوية ي التي يصنعها القاطع للمنحنى مع الاتجاه الموجب لمحور السينات بزاوية ميل المستقيم، ويكون ظا ي = ميل القاطع).

مثال (2)

إذا قطع المستقيم ل منحنى الاقتران ق (س) = س + جا 2س، في النقطتين (0، ق(س))، (90، ق90). احسب:

1. ميل المستقيم ل
2. قياس زاوية ميل المستقيم ل

الحل

ميل المستقيم ل = متوسط التغير في الاقتران ق (س) في الفترة (0، 90)

ميل المستقيم = ق (90) – ق(0) ÷ (90 – 0) = ((90+ جا 2×90) – (0 + جا 0)) ÷ (90) = 90 ÷ 90 =1

بما أن ميل المستقيم = ظا ي = 1ـ، إذن ي = 45 درجة. (لأن ظا 45 = 1).

المعنى الفيزيائي لمتوسط التغير

لو افترضنا أنه لدينا اقتران ف = ق (ن)، والذي يمثل العلاقة بين المسافة (ف) والزمن (ن) لحركة جسم في خط مستقيم بحيث أنه يقطع مسافة مقدارها ف = ف₂ – ف₁ خلال فترة زمنية ن = ن₂ – ن₁، فإنه يمكن التعبير عن متوسط التغير في المسافة (ف) عندما تتغير (ن) من ن₁ إلى ن₂:

متوسط التغير = ∆ ف / ∆ ن = (ف₂ – ف₁) / (ن₂ – ن₁) = (ق(ن₂) – ق(ن₁)) / (ن₂ – ن₁)

ولكن من المعروف أن حاصل قسمة المسافة على الزمن هو كمية فيزيائية = السرعة المتوسطة. لذا فإن متوسط التغير للاقتران ف = ق (ن) يُسمى السرعة المتوسطة خلال الفترة [ن₁، ن₂].

مثال (3)

يتحرك جسم على خط مستقيم، بحيث أن بُعده (ف) عن النقطة (و) بعد (ن) من الثواني يُعطى بالقاعدة ف = ق (ن) = ن ² + 8 ن. احسب:

1. السرعة المتوسطة في الفترة [0، 3]
2. السرعة المتوسطة في الفترة [1، أ] تساوي 13 متر/ثانية، جد قيمة أ.

الحل

لدينا ن₁ = 0 وكذلك ن₂ = 3

السرعة المتوسطة = ∆ ف / ∆ ن = (ق(ن₂) – ق(ن₁)) / (ن₂ – ن₁) = (ق(3) – ق(3)) / (3 – 0)

السرعة المتوسطة = (3 ² + 8 × 3 – صفر ) / 3 = 33 /3 = 11 متر / ثانية.

السرعة المتوسطة = ∆ ف / ∆ ن = (ق(أ) – ق(1)) / (أ – 1) = (أ ² + 8 أ – 9) / أ = 13

بالتبسيط نحصل على: أ ² – 5 أ + 4 = صفر، وبحل المعادلة نحصل على قيمة أ = 4.