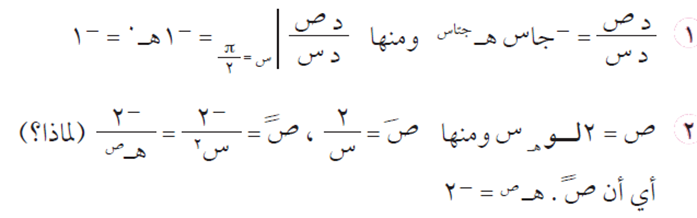6. قاعدة السلسلة

6. قاعدة السلسلة #

إذا كانت ص = ق(ع)، ع = ه(س(، وكان ه(س) قابلًا للاشتقاق، وكان ق(س) قابلًا للاشتقاق عند ه(س)، وكان مدى ه ⊇ مجال ق، فيكون:

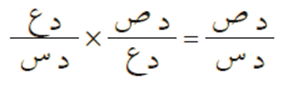
أي أن:

مشتقة ص بالنسبة لـ س نساوي = مشتقة ص بالنسبة لـ ع × مشتقة ع بالنسبة لـ س

أو بمعنى آخر:

مشتقة دالة الدالة = المشتقة حسب قاعدة السلسلة = مشتقة الاقتران الأصلي × مشتقة ما بداخل الاقتران

أو بالرموز:

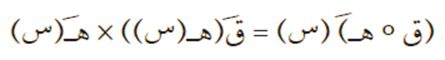
حيث (ق ∘ ه) (س) = ق (ه(س)) وهو الاقتران المركّب من ق، ه.

مثال (1) #

إذا كان ق(س) = س ^٣ + س، ه(س) = س ^٢، جد:

1. (ق ∘ ه)^/ (س)
2. (ه ∘ ه)^/ (٢(

الحل

ق^/(س) = ٣س ^٢ + ١، ه^/(س) = ٢س

1. (ق ∘ ه)^/(س) = ق^/(ه(س)) × ه^/(س(

وبالتعويض المباشر يكون لدينا:

(ق ∘ ه)^/(س) = ق^/(س²) × 2 س =  (٣ (س ²)² + 1) × 2 س = 6 س ⁵ + 2 س

• (ه ∘ ه)^/ (2) = ه^/(ه(2)) × ه^/(2)

وبالتعويض المباشر يكون لدينا:

(ه ∘ ه)^/ (2) = هَ(4) × ه^/(2) = 8 × 4 = 32.

مثال (2) #

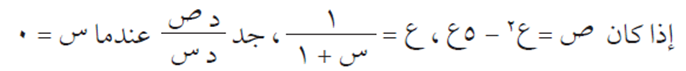
الحل

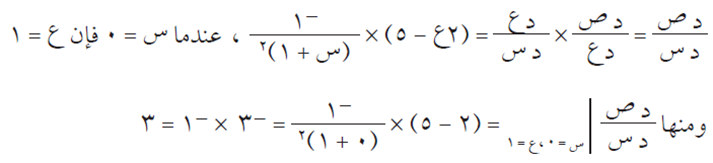
نتيجة #

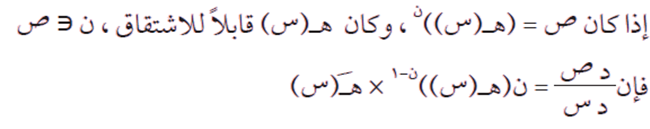
مثال (3) #

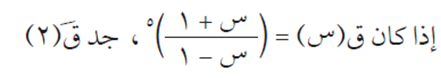
الحل

بتطبيق قاعدة السلسلة، نحصل على:

المشتقة = مشتقة الأقواس × مشتقة ما بداخل الأقواس

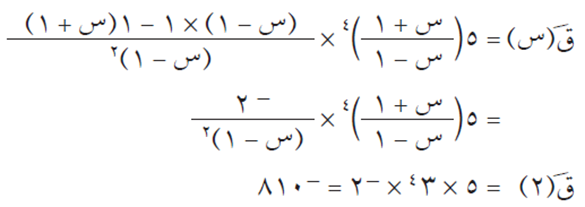
ملاحظة #

يمكن تعميم قاعدة السلسلة لتشمل أكثر من اقترانين.

مثال (4) #

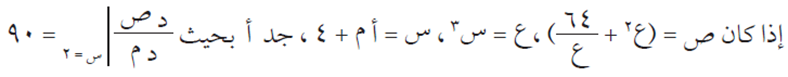
الحل

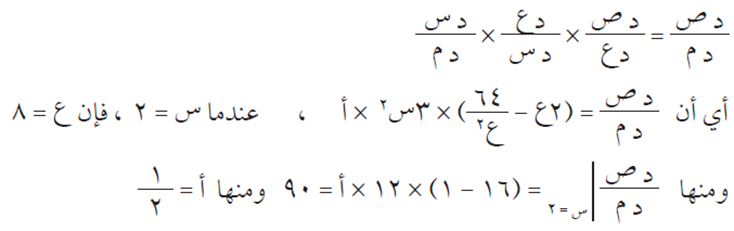
قاعدة #

إذا كان ك(س) اقترانًا قابلًا للاشتقاق، فإن:

مثال (5) #

الحل