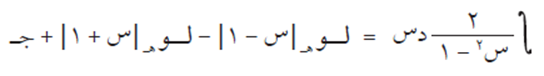طرق التكامل #
أولاً: التكامل بالتعويض #
من طريقة الاشتقاق الضمني، يمكن استنتاج أنه إذا كان ه(س) = ع فإن:
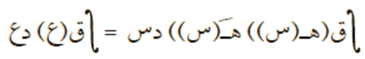
علمًا بأن ق(س)، ه(س) اقترانان متصلان.
مثال (1) #
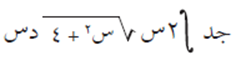
الحل
نفرض أن: ع = س٢ + ٤ إذن د ع = ٢ س د س ومنها د س = د ع / ٢ س.
وبالتعويض، ينتج أن:
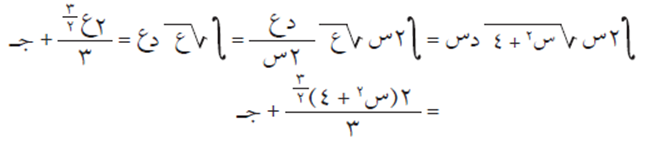
نتيجة #
إذا كان ق(س) اقترانًا قابلًا للتكامل فإن:
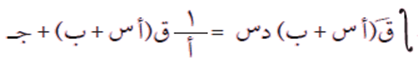
حيث أ، ب، ج أعدادًا حقيقية، أ ≠صفر.
مثال (2) #
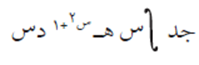
الحل
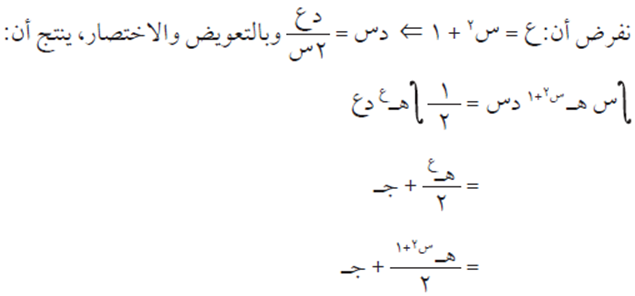
قاعدة #
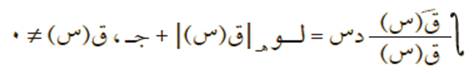
مثال (3) #
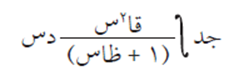
الحل
بما أن البسط يساوي مشتقة المقام، إذن نطبق القاعدة كما يلي:
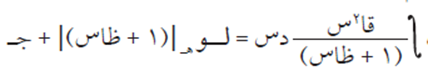
ثانيًا: التكامل بالأجزاء #
نعلم أن مشتقة حاصل ضرب اقترانين = الأول × مشتقة الثاني + الثاني × مشتقة الأول، أي أن:
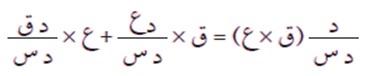
وبأخذ التكامل للطرفين بالنسبة إلى س، نحصل على:
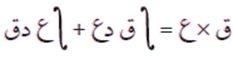
ومنها يكون:
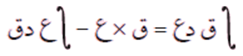
تُسمى هذه النتيجة قاعدة التكامل بالأجزاء، وتستخدم لإيجاد تكامل بعض الاقترانات التي تكون على صورة حاصل ضرب اقترانين ليس أحدهما مشتقة للآخر، باعتبار أنهما جزئين.
قاعدة التكامل بالأجزاء #
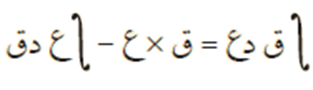
مثال (4) #
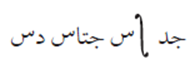
الحل
نفرض أن الجزء الأول هو الاقتران ق = س
ونفرض أن الجزء الثاني هو دع = جتا س دس
وبالتالي يكون لدينا:
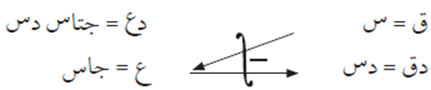
وبحسب القاعدة:
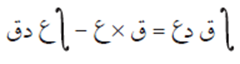
يكون:
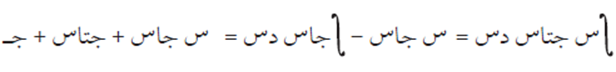
ثالثًا: التكامل بالكسور الجزئية #
لقد تعلمت في درس السابقة إيجاد التكامل التالي بطريقة التكامل بالتعويض، وذلك عندما يكون البسط هو مشتقة المقام:
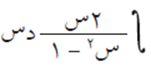
ولكن ماذا لو لم يكن البسط مشتقة للمقام، مثل التكامل التالي:
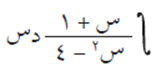
في مثل هذه الحالة نلجأ لطريقة جديدة تسمى التكامل بالكسور الجزئية، وسوف نقتصرها على الاقترانات النسبية، التي يمكن كتابة المقام فيها على شكل حاصل ضرب ثلاثة عوامل خطية مختلفة على الأكثر.
خطوات كتابة الاقتران بصورة الكسور الجزئية #
مطلوب كتابة الاقتران التالي على صورة كسور جزئية:
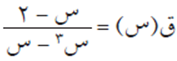
لكتابة هذا الاقتران على صورة كسور جزئية، نقوم بتحليل المقام إلى عوامله الأولية، ثم نقوم بكتابة الاقتران ق(س) على الصورة التالية:
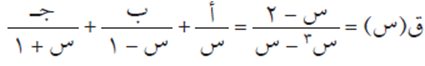
ثم بتوحيد المقامات، والإفادة من تساوي الاقترانات، نحصل على المعادلة التالية:
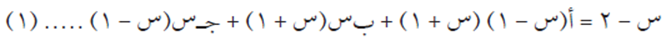
ولتحديد قيم أ، ب، ج نقوم بما يلي:
نعوض عن س = 1 في المعادلة (1)، ومنها ب = -1/2
نعوض عن س = – 1 في المعادلة (1)، ومنها جـ = -3/2
ولإيجاد قيمة أ نعوض عن س = صفر في المعادلة (1) ومنها أ = 2
فيصبح لدينا:
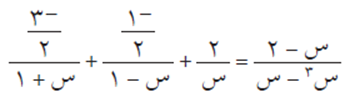
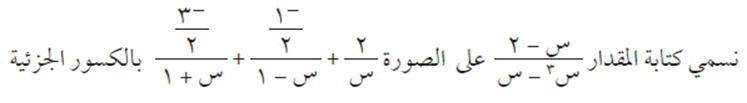
ملاحظة #
إذا أمكن كتابة الاقتران النسبي على الصورة:
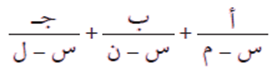
حيث أ ، ب ، ج أعداداً حقيقية، فإن تكامله يساوي:
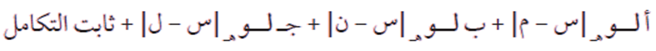
ويُراعى في ذلك أن تكون درجة البسط أقل من درجة المقام.
أما إذا كانت درجة البسط ≤ درجة المقام نستخدم القسمة المطولة.
مثال (1) #
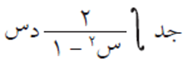
الحل
بما أن درجة البسط أقل من درجة المقام، وأن البسط ليس مشتقة للمقام لذلك يمكن كتابة الكسر كما يلي:
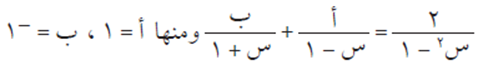
وبتكامل الطرفين بالنسبة إلى س:
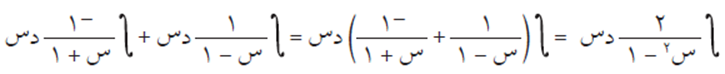
ومنها: