4. التقعّر ونقط الانعطاف

4. التقعّر ونقط الانعطاف #

تعريف التقعّر #

يُقال لمنحنى الاقتران ق(س) أنه مقعّر للأعلى في الفترة [أ، ب] إذا كان واقعًا فوق جميع مماساته في الفترة ]أ، ب[، ويُقال أنه مقعّر للأسفل في الفترة [أ، ب] إذا كان واقعًا تحت جميع مماساته في الفترة ]أ، ب[.

اختبار التقعّر باستخدام المشتقة الثانية

إذا كان ق(س) اقترانًا متصلًا في الفترة ]أ، ب[، وكان ق^//(س) معرفًا في الفترة ]أ، ب[ فإن منحنى ق(س) يكون:

1. مقعّرًا للأعلى في الفترة ]أ، ب[.إذا كانت ق^//(س) < صفر لجميع قيم س ϶ ]أ، ب[.
2. مقعّرًا للأسفل في الفترة ]أ، ب[ إذا كانت ق^//(س) < صفر لجميع قيم س ϶ ]أ، ب[.
3. غير مقعّر للأعلى أو للأسفل في الفترة ]أ، ب[ إذا كانت ق^//(س) = صفر لجميع قيم س ϶ ]أ، ب[.

مثال (1) #

جد مجالات التقعّر للأعلى وللأسفل لمنحنى الاقتران ق(س) = 3 س² – س³، س ϶ ]- 2، 5[.

الحل

ق(س) متصل في الفترة ]- 2، 5[ لأنه كثير حدود.

ق^/(س) = 6 س – 3 س²

ق^//(س) = 6 – 6 س

بوضع ق^//(س) = صفر يكون: 6 – 6 س = صفر، أي أن: س = 1.

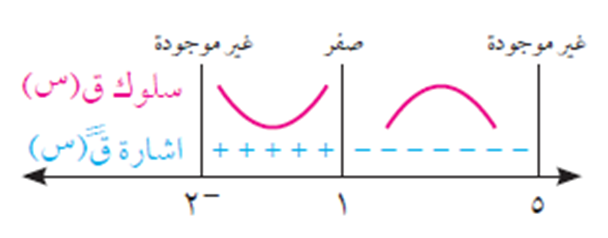
ومن إشارة ق^//(س) في الشكل أعلاه، يكون منحنى ق(س) مقعّرًا للأعلى في الفترة ]- 2، 1[، ومقعّرًا للأسفل في الفترة ]1، 5[.

تعريف نقطة الانعطاف #

1. تسمى النقطة (جـ ، ق(جـ)) نقطة انعطاف للاقتران ق(س) إذا كان:
   • ق(س) اقترانًا متصلًا عند س = جـ
   • يغير الاقتران اتجاه تقعّر منحناه عند س = ج من الأعلى إلى الأسفل، أو العكس.
2. زاوية الانعطاف: هي زاوية ميل المماس المرسوم لمنحنى ق(س) عند نقطة الانعطاف.
3. إذا كانت (جـ ، ق(جـ)) نقطة انعطاف، وكان ق/(جـ) = صفر، فتسمى النقطة (جـ ، ق(جـ)) نقطة انعطاف أفقي.

مثال (2) #

جد نقاط الانعطاف (إن وجدت) للاقتران ق(س) = 3 جاس جتاس، س ϶ ]0، π[.

الحل

قَ^/(س) = -3 جا²س + 3 جتا²س = 3 جتا 2س، س ϶ ]0، π[.

ق^//(س) = – ٦جا ٢س

نجعل ق//(س) = صفر، فيكون: – 6 جا 2 س = صفر، ومنها س = π/2.

وبما أن ق(س) متصل عند س = π/2 ويغير من اتجاه تقعّره عندها (كما تشير إشارة ق^//(س) في الشكل أعلاه(، فإن النقطة (π/2، ق(π/2)) = (π/2، صفر) هي نقطة انعطاف أفقي (من التعريف).

ملاحظة #

إذا كان ق(س) كثير حدود وكانت (س₁، ق(س₁)) نقطة انعطاف للاقتران ق(س)، فإن ق^//(س_١) = صفر.

اختبار المشتقة الثانية في تعيين القيم القصوى (نظرية) #

إذا كان ق(س) اقترانًا قابلًا للاشتقاق في فترة مفتوحة تحوي جـ وكان ق^/(جـ) = صفر فإن:

1. ق(جـ) قيمة عظمى محلية، إذا كانت ق^//(جـ) < صفر.
2. ق(جـ) قيمة عظمى محلية، إذا كانت ق^//(جـ) > صفر.
3. يفشل تطبيق الاختبار إذا كانت قَ^//(جـ) = صقر، أو ق^//(جـ) غير موجودة.

مثال (3)

جد القيم العظمى والصغرى المحلية للاقتران ق(س) = 3 س⁴ – 8 س³ + 6 س²، باستخدام اختبار المشتقة الثانية (إن أمكن).

الحل

ق(س) متصل وقابل للاشتقاق في ح لأنه كثير حدود.

ق^/(س) = 12 س³ – 24 س² + 12 س

عندما ق (س) = صفر، يكون:

12 س³ – 24 س² + 12 س = صفر

12 س (س² – 2 س + 1) = صفر

12 س (س² – 1) = صفر

ومنها إما س = صفر أو س = 1

ق^//(س) = 36 س² – 48 س + 12

ق^//(صفر) = 12 وهي قيمة > صفر، إذن ق(صفر) = صفر هي قيمة صغرى محلية.

بما أن ق^//(1) = صفر، لذلك لا نستطيع تحديد نوع القيمة القصوى ق(1) باستخدام اختبار المشتقة الثانية، لذا نلجأ إلى اختبار المشتقة الأولى.

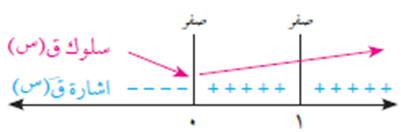
من الشكل أعلاه، لا يوجد قيمة قصوى محلية عند س = 1.