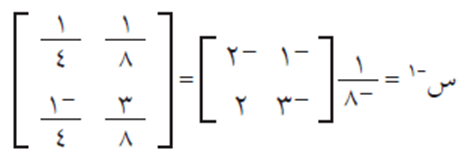4. النظير الضربي للمصفوفة المربعة #
تعريف النظير الضربي للمصفوفة #
تسمى المصفوفة المربعة أ مصفوفة غير منفردةٍ إذا وُجدت مصفوفة مربعة ب من نفس الرتبة بحيث يكون أ × ب = ب × أ = المصفوفة المحايدة م، وتسمى المصفوفة ب النظير الضربي للمصفوفة أ، ونرمز لها بالرمز أ -١ ونكتب ذلك كما يلي:
ب = أ -١
ويكون:
أ × ب = ب × أ = المصفوفة المحايدة م
مثال (1) #
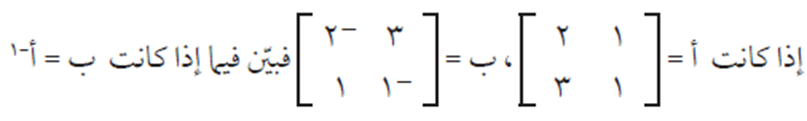
الحل
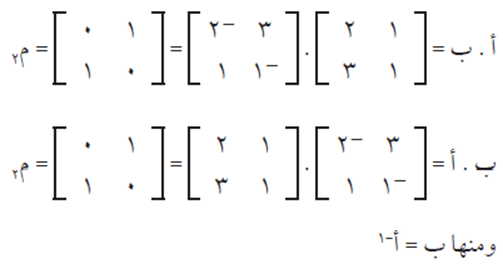
تعريف المصفوفة المنفردة #
المصفوفة المنفردة هي المصفوفة المربعة التي لا يوجد لها نظير ضربي.
نظرية #
المصفوفة أ منفردة إذا وفقط إذا كان | أ | = صفر.
خصائص النظير الضربي للمصفوفة #
إذا كانت أ ، ب مصفوفتين مربعتين، وغير منفردتين، ومن نفس الرتبة، وكان ك عدد حقيقي ≠ ٠، فإن:
- ( أ – ١ ) – ١ = أ
- ( ك أ ) – ١ = 1/ك × ( أ – ١ )
- ( أ × ب ) – ١ = ب – ١ × أ – ١
إيجاد النظير الضربي للمصفوفة #
سوف نتعرف على طرق إيجاد النظير الضربي للمصفوفة المربعة، وستقتصر دراستنا على النظير الضربي للمصفوفات المربعة من الرتبة الثانية فقط.
مثال (2) #
جد النظير الضربي للمصفوفة أ، حيث:
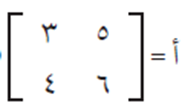
الحل
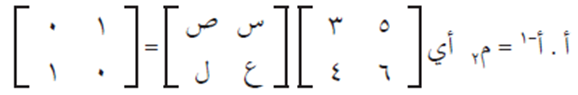
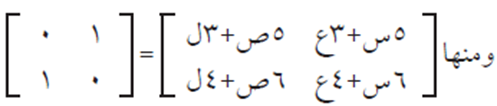
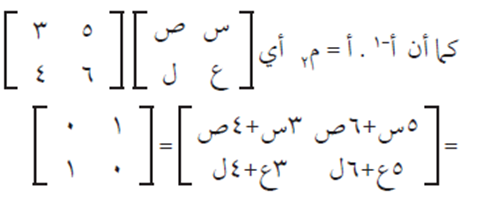
وبحل المعادلات الناتجة من تساوي المصفوفتين في الحالتين السابقتين، ينتج أن:
س = 2 ، ع = – 3 ، ص = -3/2 ، ل = 5/2
أي أن المعكوس الضربي يساوي:
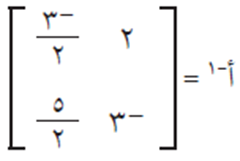
تعميم #

أي أن المعكوس الضربي أ – ١ ينتج من ضرب المصفوفة أ بمقلوب محددها بعد تبديل أماكن مدخلات القطر الرئيسي وتغيير إشارة مدخلات القطر الآخر (الثانوي) من المصفوفة أ.
مثال (3) #
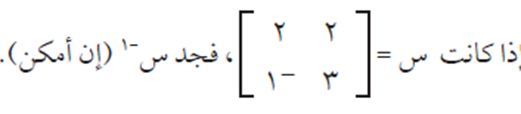
الحل
| س | = – 2 – 6 = – 8
إذن يوجد نظير ضربي للمصفوفة س. وهو كما يلي: