3. المحددات #
تعريف محدد المصفوفة #
محدد المصفوفة المربعة أ التي رتبتها 2×2 هو عدد ينتج عن حاصل ضرب عناصر القطر الرئيسي في المصفوفة مطروحًا منه حاصل ضرب عناصر القطر الثانوي، ويُرمز للمحدد بالرمز | أ |.
أي أنه إذا كان لدينا المصفوفة أ بحيث:
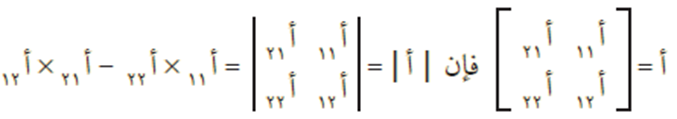
وإذا كانت رتبة المصفوفة أ هي 3 × 3، كما يلي:
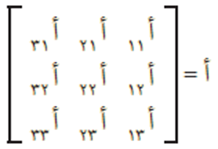
فإن محدد المصفوفة أ يساوي | أ | وتكون قيمته كما يلي:
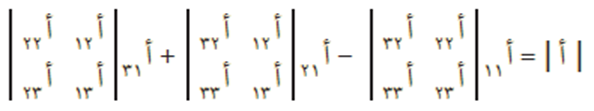
أما إذا كانت رتبة المصفوفة أ هي 1 × 1 (أي أنها تتكون من مدخلة واحدة أ 11)، فإن محدد المصفوفة أ يساوي | أ | = قيمة المدخلة الوحيدة = أ 11.
مثال (1) #
إذا كان:
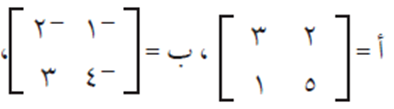
فجد: | أ |، | ب |ـ، | أ + ب |
الحل
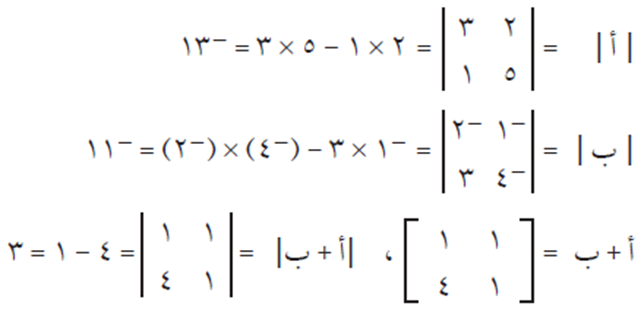
نلاحظ من النتائج أعلاه أن في جمع المحددات، | أ | + | ب | ≠ | أ + ب |.
نظرية #
إذا كانت أ مصفوفة مربعة من الرتبة الثالثة، فإنه يمكن إيجاد محددها | أ | بدلالة مدخلات أي صف، أو أي عمود فيها، وذلك بضرب تلك المدخلات بالمحدد الناتج من تصور شطب الصف ي والعمود ه، وإعطاء إشارة لحاصل الضرب بحسب القاعدة (- ١) ي+ه.
مثال (2) #
جد قيمة المحدد التالي باستخدام التعريف وبدلالة مدخلات العمود الثاني:
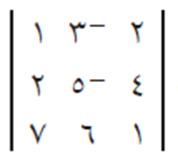
الحل
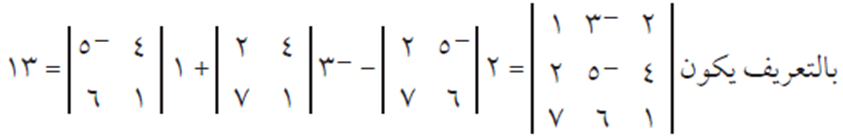
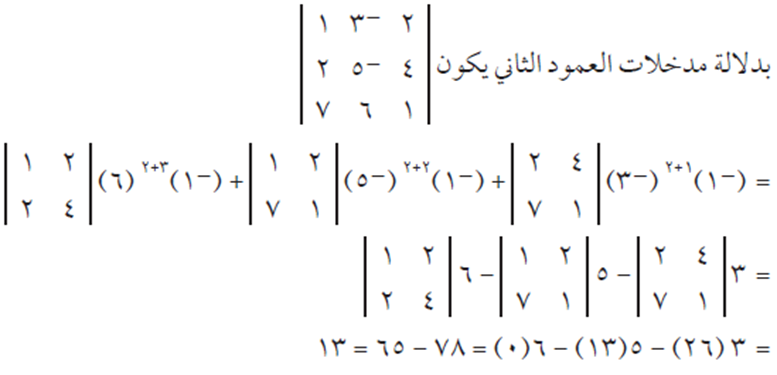
بعض خصائص المحددات #
يلزمنا في كثير من الحالات حساب قيم المحددات بصورة سريعة، وخاصة عندما تكون المدخلات أعداد كبيرة. ولتحقيق ذلك، وتوفيرًا للوقت والجهد، سوف نتعرف على بعض خصائص المحددات التي يمكن استخدامها لتحقيق هذا الغرض:
- عند تبديل صف مكان صف، أو عمود مكان آخر، فإن قيمة المحدد تًضرب × ( – 1). مثلًا:
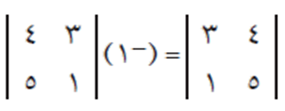
- يمكن إخراج عامل مشترك من أي صف، أو أي عمود، وذلك بإخراج العدد 3 كعامل مشترك لمدخلات الصف الثالث وضربه بمحدد المصفوفة الناتجة كما في المثال التالي:
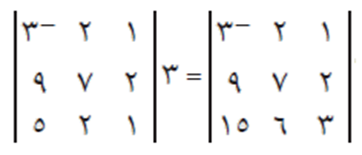
- إذا أضيف لمدخلات أي صف، أو أي عمود مضاعفات نظائرها في صف آخر، أو عمود آخر، فلا تتغير قيمة المحدد. فمثلًا، يضرب مدخلات الصف الثاني × ٤ وإضافتها لنظائرها في مدخلات الصف الأول قي المثال التالي:
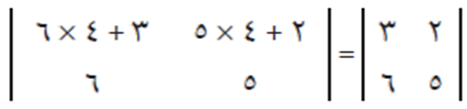
- إذا تساوت المدخلات المتناظرة في صفين أوفي عمودين في مصفوفة فإن محددها يساوي صفر. مثلًا المحدد التالي قيمته تكون مساوية صفر:
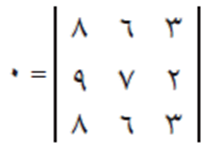
- إذا كانت المصفوفة مصفوفة مثلثية علوية فإن محددها يساوي حاصل ضرب المدخلات على القطر الرئيسي. فمثلًا، إذا كان لدينا المصفوفة أ حيث:
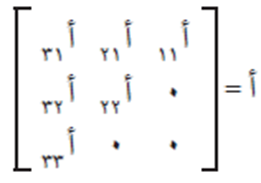
فإن المحدد | أ | = أ 11 × أ 22 × أ 33
قاعدة (1) #
إذا كانت أ مصفوفة مربعة من الرتبة ن، فإن |ك أ| = ك ن | أ |، حيث ك ∋ ح.
وتفسير هذه القاعدة يتضح من قيمة محدد المصفوفة الناتجة عن ضربها بعدد حقيقي، حيث أننا نقوم بضرب جميع عناصر المصفوفة بهذا العدد، وبالتالي فإن المحدد الخاص بها سوف يتضاعف بنفس الطريقة بالضرب في العدد ك عدد ن من المرات (رتبة المصفوفة).
قاعدة (2) #
إذا كانت أ، ب مصفوفتين مربعتين من الرتبة ن فإن | أ . ب | = | أ | × |ب|
مثال (3) #
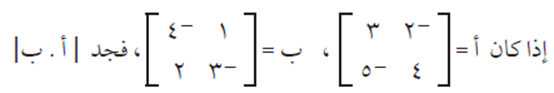
الحل
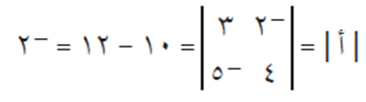
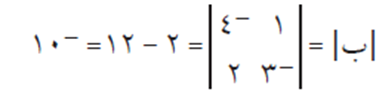
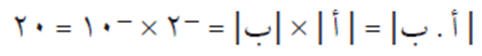
كما يمكن إيجاد المصفوفة أ . ب أولًا ثم حساب قيمة محددها | أ . ب |، والتحقق من النتيجة.



