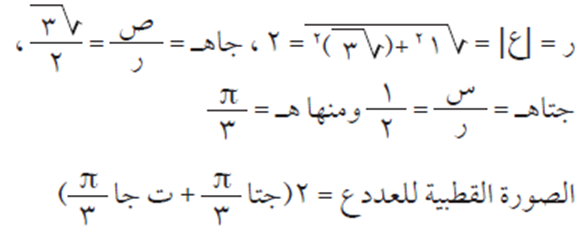قسمة الأعداد المركبة
تعريف مقياس العدد المركب
إذا كان لدينا العدد المركب ع = س + ص ت، فإننا نسمي المقدار س٢ + ص٢ مقياس العدد المركب ع ويُرمز له بالرمز | ع |. أي أن: | ع | = س ٢ + ص ٢
تعريف مرافق العدد المركب
إذا كان لدينا العدد المركب ع = س + ص ت، فإننا نسمي العدد س – ص ت مرافق العدد المركب ع ويُرمز له بالرمز ع. أي أن (عين بار): ع = س – ص ت.
مثال (1)
إذا كان ع = ٣ + ٤ ت، جد: ع ، | ع | ، | ع |
الحل
ع = ٣ – ٤ ت
| ع | = | ٣ + ٤ ت | = جذر (٣ ٢ + ٤ ٢) = ٥
| ع | = | ٣ – ٤ ت | = جذر (٣ ٢ + ٤ ٢) = ٥
خصائص المقياس، والعدد المرافق للعدد المركب
إذا كان ع ϶ ك فإن:
- ( ع/ )/ = ع
- ع
ع=عع = |ع|٢ - | ع | = |
ع| - |ج ع| = |ج| |ع|، ج ϶ ح
- إذا كان ع = أ + ب ت فإن ع +
ع= ٢ أ، ع –ع= ٢ ب ت - إذا كان ع ١، ع ٢ ϶ ك، فإن | ع ١ ع ٢| = |ع ١| |ع ٢|
- إذا كان ع ١، ع ٢ ϶ ك، ع ٢ ≠ صفر فإن:
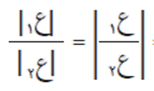
تعريف قسمة الأعداد المركبة
إذا كان ع ١، ع ٢ ϶ ك، وكانت ع 2 ≠ صفر، فإن حاصل قسمة العددين المركبين ع1، ع2 يكون:
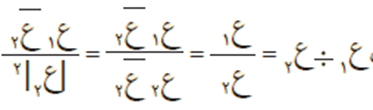
نتيجة
إذا كان ع ≠ صفر، فإن:
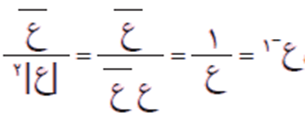
مثال (2)
- باستخدام الضرب في المرافق
- باستخدام النظير الضربي
الحل
باستخدام الضرب في المرافق:
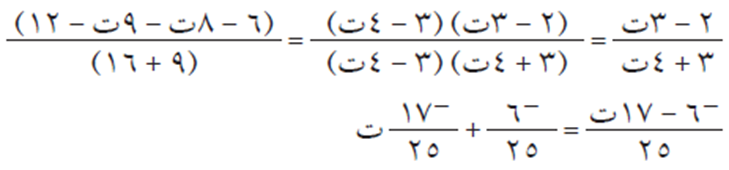
باستخدام النظير الضربي:
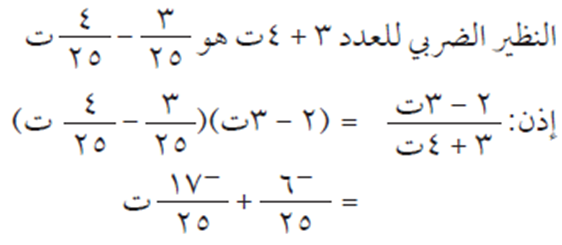
التمثيل البياني للأعداد المركبة
يمكن تمثيل العدد المركب ع = س + ص ت بيانيًا في المستوى الديكارتي بالنقطة، أ (س، ص).
مثلًا، العدد المركب 3 + ت يمكن تمثيله بالنقطة أ (3، 1) في المستوى كما في الشكل أدناه.
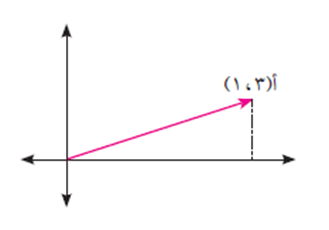
يسمى هذا المستوى الإحداثي بالمستوى المركب أو مستوى أرجاند.
التمثيل القطبي للأعداد المركبة
بما أنه يمكن تمثيل العدد المركب ع = س + ص ت بيانيًا في مستوى الأعداد المركبة بالنقطة، أو الزوج المرتب (س، ص). كما أن كل زوج مرتب، يمكن تمثيله بمتجه قياسي بدايته النقطة (صفر، صفر)، ونهايته النقطة (س، ص) ويصنع زاوية مقدارها ه مع الاتجاه الموجب لمحور السينات (المحور الأفقي).
وتسمى ه السعة الأساسية للعدد المركب، حيث ظاهـ = ص/س، صفر ≥ ه > 2π، كما في الشكل أدناه.
ويكون طول المتجه = ر ويساوي مقياس العدد المركب ع = س + ص ت حيث ر = |ع| = جذر (س٢ + ص٢ ).
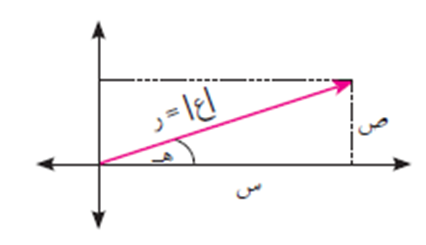
نلاحظ من الشكل أعلاه أن س = ر جتا هـ، ص = رجا ه. وبذلك فإن العدد ع = س + ص ت يمكن كتابته على الصورة ع = ر (جتا ه + ت جا ه) ويسمى هذا التمثيل بالتمثيل القطبي للعدد المركب.
تعريف الصورة القطبية للعدد المركب
الصورة القطبية للعدد المركب ع = س + ص ت، ع ≠ صقر هي: ع = ر (جتا ه + ت جا ه)، حيث:
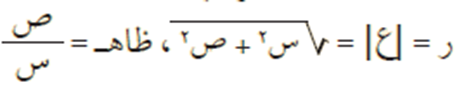
مثال (3)
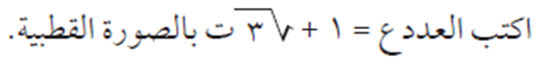
الحل