3. القيم القصوى
تعريف القيم الصغرى والعظمى المحلية:
ليكن ق)س) اقتران معرف على المجال ع، ولتكن جـ ϶ع، عندها يكون للاقتران ق(س):
- قيمة عظمى محلية عند س = جـ هي ق(جـ) إذا وُجدت فترة مفتوحة (ف) تحوي جـ، بحيث أن ق(جـ) ≤ ق(س) لجميع قيم س ϶ (ف ∩ ع).
- قيمة صغرى محلية عند س = جـ هي ق(جـ) إذا وُجدت فترة مفتوحة (ف) تحوي جـ، بحيث أن ق(جـ) ≥ ق(س) لجميع قيم س ϶ (ف ∩ ع).
- قيمة عظمى مطلقة عند س = جـ هي ق(جـ) إذا كانت ق(جـ) ≤ ق(س) لجميع قيم س ϶ ع.
- قيمة صغرى مطلقة عند س = جـ هي ق(جـ) إذا كانت ق(جـ) ≥ ق(س) لجميع قيم س ϶ ع.
ملاحظة: تسمى كل من القيم العظمى والقيم الصغرى قيمًا قصوى، سواء أكانت محلية أو مطلقة.
مثال (1)
يمثل الشكل التالي منحنى الاقتران ق(س) في الفترة ع = [- 2، 2]. اعتمد عليه في إيجاد القيم القصوى المحلية والمطلقة (إن وجدت). ثم جد قيمة المشتقة الأولى عند كل قيمة منها (إن وجدت).
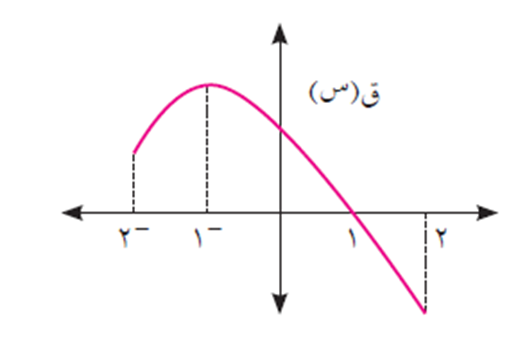
الحل
يوجد للاقتران ق(س) قيمة صغرى محلية عندما س = – 2 هي ق(- 2(، لأنه يوجد فترة مفتوحة مثل ف = ] -3، -1[ تحوي العدد – 2 بحيث أن ق(- 2) ≥ ق(س) ⩝ س ϶ ف ∩ [- 2، 2]
كما أن ق/(- 2) غير موجودة.
ق(- ١) قيمة عظمى محلية وهي مطلقة لأن ق(- ١) ≤ ق(س) ⩝ س ϶ [- 2، 2].
ق/(-١) = صفر.
ق(2) قيمة صغرى محلية وهي مطلقة لأن ق(2) ≥ ق(س) ⩝ س ϶ [- 2، 2].
ق/(2) غير موجودة.
تعريف النقطة الحرجة
تسمى النقطة (أ، ق(أ))، ق نقطة حرجة للاقتران ق(س) إذا كانت:
- أ ϶ مجال ق(س)
- ق/(أ) = صفر أو ق/(أ) غير موجودة.
مثال (2)
عيّن جميع النقط الحرجة للاقتران التالي:
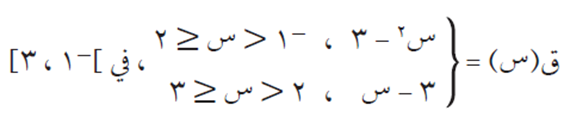
الحل
ق(س) متصل عند س = 2
ق/(2) غير موجودة، ق/(3) غير موجودة.
نجعل ق/(س) = صفر، ومنها س = صفر ϶ ] -1، 2[
لا يوجد قيم لِ س ϶ ] -1، 2[ بحيث تكون ق/(س) = صفر.
لا يوجد نقطة حرجة عند س = – 1 لأنها لا تنتمي إلى مجال ق(س).
ومنها تكون النقاط الحرجة هي: (صفر،-3)، (2، 1)، (3، صفر).
اختبار المشتقة الأولى لتعيين القيم القصوى
إذا كان ق(س) اقترانًا متصلًا في الفترة [أ، ب] وكانت (جـ، ق(جـ)) نقطة حرجة للاقتران ق(س)، وكانت جـ ϶ ]أ، ب[.فإنه:
- إذا كان ق/(س) > صفر عندما أ < س < جـ ، وكان ق/(س) < صفر عندما جـ < س < ب ، فإن ق(جـ) تكون قيمة عظمى محلية للاقتران ق(س).
- إذا كان ق/(س) < صفر عندما أ < س < جـ ، وكان ق/(س) > صفر عندما جـ < س < ب ، فإن ق(جـ) تكون قيمة صغرى محلية للاقتران ق(س).
مثال (3)
جد القيم القصوى المحلية للاقتران ق(س) = س3 + س2 – 5 س – 5
الحل
ق(س) اقتران متصل على ح لأنه كثير حدود.
ق/(س) = 3 س2 + 2 س – 5، لكل س ϶ ح، نجعل ق(س) = صفر، ومنها يكون:
3 س2 + 2 س – 5 = صفر، أي أن (3 س + 5)(س – 1) = صفر، إذن س = -5/3 أو س = 1.
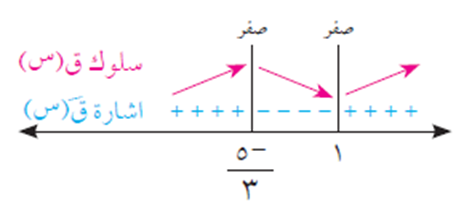
ومن إشارة ق/(س) في الشكل أعلاه تكون:
ق (-5/3) = 40/27 هي قيمة عظمى محلية للاقتران ق(س)
ق(1) = – 8 هي قيمة صغرى محلية للاقتران ق(س)
اختبار أطراف الفترة
إذا كان ق(س) اقترانًا متصلًا في الفترة [أ، ب] وقابلًا للاشتقاق في الفترة ]أ، ب[ فإن:
ق(أ) قيمة صغرى محلية، إذا كانت ق/(س) > صفر عندما س > أ (بداية تزايد).
ق(أ) قيمة عظمى محلية، إذا كانت ق/(س) < صفر عندما س > أ (بداية تناقص).
ق(ب) قيمة عظمى محلية، إذا كانت ق/(س) > صفر عندما س < ب (نهاية تزايد).
ق(ب) قيمة صغرى محلية، إذا كانت ق/(س) < صفر عندما س < ب (نهاية تناقص).
مثال (4)
جد مجموعة قيم س للنقط الحرجة للاقتران ق(س) التالي، وحدد القيم القصوى المحلية له.
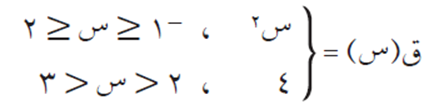
الحل
ق(س) اقتران متصل في الفترة [-1، 3[
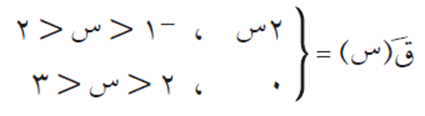
أولًا: عندما س ϶ ] -1، 2[ نجعل ق/(س) = صفر، فيكون: 2 س = صفر ومنها عند س = صفر يوجد نقطة حرجة.
ثانيًا: عندما 2 < س < 3 تكون ق/(س) = صفر، وهذا يعني أنه عند كل س ϶ ] 2، 3[ يوجد نقطة حرجة.
ق/(2) غير موجودة، ق/(- 1) غير موجودة.
فتكون مجموعة قيم س للنقط الحرجة هي {صفر، – 1، ]2، 3[}.
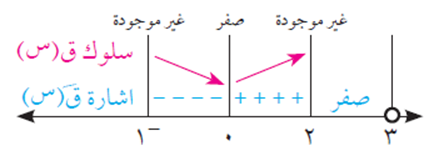
ومن إشارة ق/(س) في الشكل أعلاه، يكون:
عند س = – 1 يوجد قيمة عظمى محلية لأنها بداية تناقص.
عند س = صفر يوجد قيمة صغرى محلية
عند س = 2 يوجد قيمة عظمى محلية
عند كل س ϶ ] 2، 3[ يوجد قيمة عظمى محلية وصغرى محلية في آن واحد.
نظرية القيم القصوى المطلقة
إذا كان ق(س) اقترانًا متصلًا في الفترة [أ، ب] فإن ق(س) يتخذ قيمه القصوى المطلقة في الفترة [أ، ب].
نتيجة
إذا كان ق(س) متصلًا على فترة في مجاله، وكان له نقطة قيمة قصوى وحيدة فهي مطلقة في تلك الفترة.





