قواعد الاشتقاق
نشاط 1
في أحد المصانع الإنتاجية يوجد خطين للإنتاج، الخط الأول ينتج عدد من عبوات الألبان تتحدد وفق الاقتران ق(ن) = ن2 + ن. والخط الثاني ينتج عدد من العبوات يتحدد وفقَ الاقتران ه(ن) = ن2 + 2ن، حيث ن زمن تشغيل خط الإنتاج بالساعات.
الحل
معدل التغير في إنتاج الخط الأول من العبوات بعد ن ساعة يساوي مشتقة الاقتران = ق/(ن) = ٢ ن + ١
معدل التغير في إنتاج الخط الثاني من العبوات بعد ن ساعة يساوي مشتقة الاقتران = ه/(ن) = ٢ ن + 2
كمية إنتاج الخطين من العبوات بدلالة ن تساوي = (ن2 + ن ) + (ن2 + 2ن) = 2 ن2 + 3 ن
معدل التغير في إجمالي إنتاج المصنع بدلالة ن يساوي مشتقة المجموع = (المجموع)/ (ن)= 4 ن + 3
وبذلك نستنتج أن: معدل التغير في إجمالي إنتاج المصنع = مجموع المشتقتين = ق/(ن) + ه/(ن).
معدل تغير الاقتران
من تعريف متوسط التغير للاقتران ص = ق (س)، عندما تتغير س من س1 إلى س1 + ∆س، لدينا:
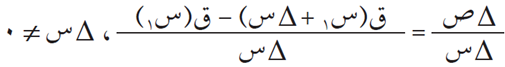
وإذا أخذنا نهاية الدالة:
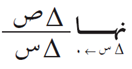
وكانت هذه النهاية موجودة فإننا نسميها معدل التغير للاقتران ق (س) عند س1، أو المشتقة الأولى للاقتران ق (س) عند س = س1، ونقول أن ق (س) قابل للاشتقاق عند س = س1، أي كلما اقتربت س من س1 (أو كلما اقتربت ∆س من الصفر) فإن متوسط تغير الاقتران (ميل القاطع الذي يمر بنقطتين مختلفتين) يؤول إلى معدل تغير الاقتران ق (س) عند نقطة س = س1 (ميل المماس الذي يمر بنقطة واحدة س1)، كما يظهر بالشكل التالي:
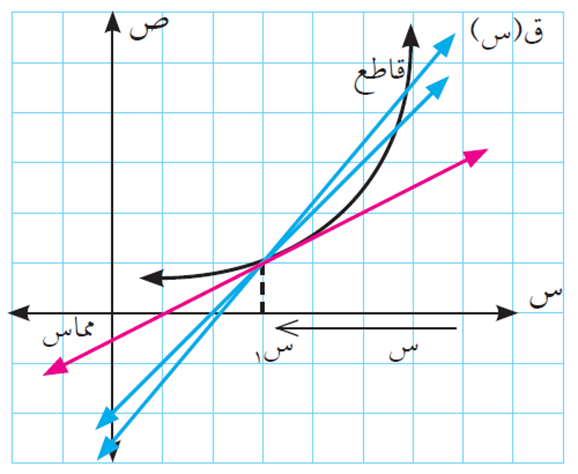
تعريف المشتقة الأولى
إذا كانت ص = ق(س) هي اقتران معرف عند س1 في مجاله، والنهاية:
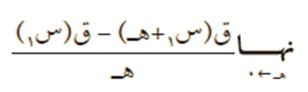
كانت موجودة، فإن هذه النهاية تُسمى المشتقة الأولى للاقتران ق (س) عند س1،ونرمز لها بأحد الرموز الآتية: قَ (س1)، أو ص/ | س = س1 ، أو بالرمز: دص/دس | س = س1
ويمكن كتابتها على النحو التالي:
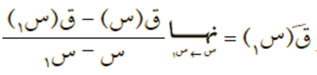
تعريف المشتقة اليُمنى والمشتقة اليُسرى
ليكن الاقتران ق (س) معرفًا عندما س = س1، فيكون:
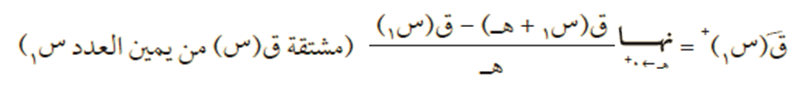
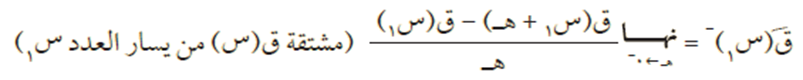
وعندما ق/(س1)+ = ق/(س1)– = ل فإن الاقتران ق(س) قابل للاشتقاق عند س1 ويكون:
ق/(س1) = ل
تعريف قابلية الاشتقاق
- إذا كان الاقتران ق (س) معرفًا على الفترة [أ، ب]، فإن ق (س) غير قابل للاشتقاق عند أطراف الفترة [أ، ب]، أي أنه غير قابل للاشتقاق عند س = أ وعند س = ب.
- يكون ق (س) قابلاً للاشتقاق عند الفترة ]أ، ب[ إذا كان قابلاً للاشتقاق عند كل نقطة فيها.
قاعدة الاشتقاق (1)
إذا كان ق (س) = جـ حيث جـ عدد حقيقي (جـ ϶ ح)، فإن ق/(س) = صفر لجميع قيم س ϶ ح.
مثال (1)
إذا كان ق(س) = 5 فإن ق/(س) = صفر
وإذا كان ق(س) جتا π فإن ق/(س) = صفر
قاعدة الاشتقاق (2)
إذا كان ق (س) = س، فإن ق/(س) = 1 لجميع قيم س ϶ ح.
قاعدة الاشتقاق (3)
إذا كان ق (س) اقتران قابل للاشتقاق، وكان جـ عدد حقيقي (جـ ϶ ح)، فإن ك(س) = جـ × ق(س) قابل للاشتقاق أيضًا ويكون كَ (س) = جـ × ق/(س).
(مشتقة عدد في اقتران = العدد في مشتقة الاقتران).
مثال (2)
إذا كان ق(س) = 5 س فإن ق/(س) = 5 س1 – 1 = 5 س صفر = 5 × 1 = 5
قاعدة الاشتقاق (4)
إذا كان ق(س)، هـ(س) اقترانين قابلين للاشتقاق، فإن ك(س) = ق(س) هـ(س) قابل للاشتقاق أيضًا ويكون ك/(س) = ق/(س) ± هـ/(س).
(مشتقة حاصل مجموع أو طرح اقترانين = مجموع أو طرح مشتقتي الاقترانين).
مع ملاحظة أن هذه القاعدة يمكن أن تنطبق على أكثر من اقترانين أيضًا.
مثال (3)
إذا كان لدينا ق/(1) = 5، ك/(1) = -3، وكان ل(س) = 2 س + ق(س) – 3 ك(س)، جد ل/(1).
الحل
بأخذ المشتقة للاقتران ل(س):
ل/(س) = 2 + ق/(س) – 3 ك/(س)
بالتعويض عن س = 1:
ل/(1) = 2 + ق/(1) – 3 ك/(1)
ل/(1) = 2 + 5 – (3 × -3) = 16
مثال (4)
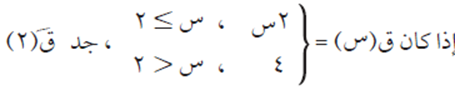
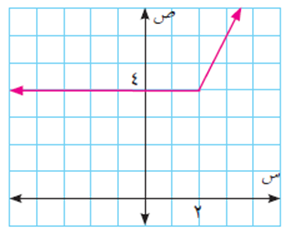
الحل
الاقتران ق(س) متصل على مجاله، لأنه معرّف على كل القيم الموجودة في مجاله، ومنها تكون المشتقة:
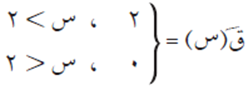
أما عند س = 2 فنبحث بالمشتقة عن يمينها وعن يسارها فتكون:
ق/(٢) + = 2، ق/(2) – = صفر
ومنها ق/(2) غير موجودة (لأن المشتقة عن اليمين لا تساوي المشتقة عن اليسار).
مثال (5)
إذا كان ق(س) =[س]، س ϶ [٠، ٢]. جد ق/(س).
الحل
نعيد كتابة ق(س) بطريقة الاقتران متعدد القاعدة كما يلي:
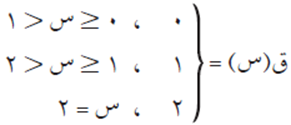
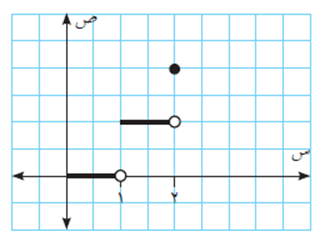
نلاحظ أن الاقتران ق(س) منفصل عند س = 1. وتكون المشتقة:
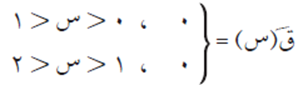
والمشتقة ق/(صفر) غير موجودة، وكذلك ق/(2) غير موجودة، لأنه من التعريف، الاقتران ق(س) معرّف على الفترة [0، 2]، فإن ق(س) غير قابل للاشتقاق عند أطرافها، أي أنه غير قابل للاشتقاق عند س = 0 وعند س = 2.
كما أن ق/(1) غير موجودة لأن الاقتران غير معرّف عند القيمة س = 1.
أتعلم
عند إيجاد المشتقة باستخدام قواعد الاشتقاق، لا بد من بحث الاتصال أولًا.
قاعدة الاشتقاق (5)
إذا كان ق(س)، هـ(س) اقترانين قابلين للاشتقاق، فإن ك(س) = ق(س) × هـ(س) قابل للاشتقاق أيضًا ويكون ك/(س) = ق(س) × هـ/(س) + هـ(س) × ق/(س)
(مشتقة حاصل ضرب اقترانين = الأول × مشتقة الثاني + الثاني × مشتقة الأول).
مثال (6)
إذا كان ق(س) = (5س – 1) (2 – س). جد ق/(س) ثم ق/(-1).
الحل
ق/(س) = (5س – 1) × (-1) + (2 – س) × 5 = – 5س + 1 + 10 – 5 س = 11 – 10 س
ويكون: ق/(-1) = 11 + 10 = 21.
مثال (7)
إذا كان ق(س) = س ك(س) جد ق/(2) علمًا بأن ق(٢) = – ٦، ك/(2) = 4.
الحل
ق/(س) = س × ك/(س) + س/ × ك(س)
ق/(س) = س × ك/(س) + 1 × ك(س)
ق/(2) = 2 × ك/(2) + 1 × ك(2)
بالتعويض عن ك/(2) = 4 ينتج:
ق/(2) = 2 × 4 + ك(2) = 8 + ك(2)
كما أنه لدينا من المعطيات:
ق(2) = – ٦ ، ق(2) = 2 × ك(2)
ومن ذلك ينتج أن: ك(2) = – 3
بالتعويض في معادلة حساب ق/(2) = 8 – 3 = 5
نظرية
إذا كان ق(س) = س ن ، فإن ق/(س) = ن × س ن – 1 ، ن ≠ 1، ن ϶ ص +، (الأعداد الصحيحة الموجبة فقط).
مثال (8)
إذا كان ق(س) = س 3 – 2 س + 5 ، جد ق/(س) ثم ق/(-2).
الحل
ق/(س) = 3 س 2 – 2
ق/(2) = 3 × (-2) 2 – 2 = 10
أتعلم
إذا كان ق(س) كثير حدود، فإن ق(س) قابل للاشتقاق.
العلاقة بين اتصال الاقتران وقابليته للاشتقاق
في جميع الأمثلة السابقة كان الاقتران المطلوب إيجاد المشتقة له اقتران متصل، أي أنه معرّف على جميع قيم س التي تنتمي لمجموعة للأعداد الحقيقية ح.
وبشكل عام فإنه إذا كان ق(س) كثير حدود فإن ق(س) قابل للاشتقاق. (لأنه يكون متصل بطبيعته وكل قيمه معرّفة).
ولكن هناك حالات خاصة يكون فيها الاقتران غير معرّف عند قيم معينة، وبالتالي فإنه يكون اقتران غير متصل ولا يمكن بالتالي إيجاد المشتقة له.
لذلك فإنه من الضروري عند إيجاد المشتقة للاقتران باستخدام قواعد الاشتقاق أن نقوم ببحث اتصال الاقتران أولاً.
نظرية
يكون ق قابلاً للاشتقاق عند س = س١ إذا وفقط إذا كان ق(س) متصلًا عند س١ وكانت المشتقة عن اليمين ق/(س١) + = المشتقة عن اليسار ق/(س1) –.
مثال (9)
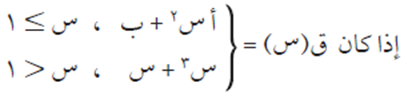
أوجد قيمة أ، ب علمًا بأن ق(س) قابل للاشتقاق على ح.
الحل
نعلم أن ق(س) متصل عند القيمة س = 1 (لأن ق(س) قابل للاشتقاق على ح ومعرّف عند س = 1)، ومنها:
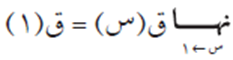
أي أن أ + ب = ٢
وبأخذ المشتقة:
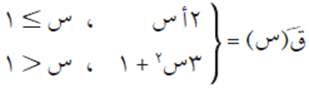
ق/(1) + = ق/(1) – ومنها ٢ أ = ٤
أي أن أ = ٢، ب = صفر.
قاعدة الاشتقاق (6)
إذا كان ق(س)، هـ(س) اقترانين قابلين للاشتقاق، فإن الاقتران:
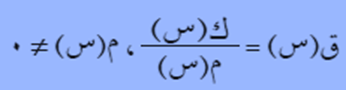
قابل للاشتقاق أيضًا ويكون:
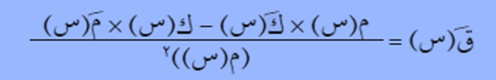
(مشتقة حاصل قسمة اقترانين = (المقام × مشتقة البسط – البسط × مشتقة المقام) / المقام تربيع).
نتيجة (1)
إذا كان ق(س) = س ن ، فإن ق/(س) = ن × س ن – 1 ، ن ≠ 1 ، ن ϶ ص. (الأعداد الصحيحة الموجبة والسالبة).
مثال (10)
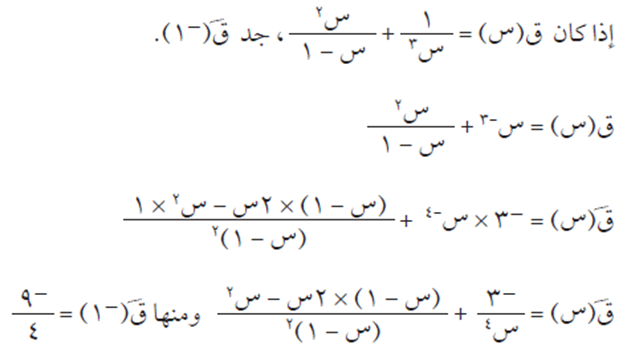
مثال (11)
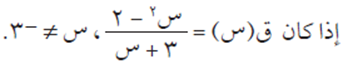
جد قيمة/قيم س التي تجعل ق/(س) = -3/4.
الحل
بتطبيق قاعدة مشتقة حاصل قسمة اقترانين:
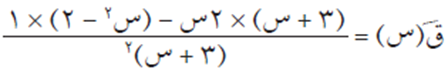
ثم بالتبسيط والاختصار، ينتج أن:
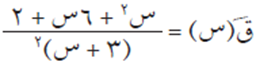
ومن المعطيات ق/(س) = – 3/4
أي أن:
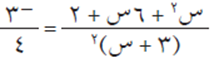
بالضرب التبادلي واختصار الناتج نحصل على:
(س + 1) × (س – 5) = صفر ومنها س = – 1 أو س = 5.
المشتقات العليا Higher Derivatives
المشتقات العليا هي المشتقات الناتجة عن تكرار الاشتقاق بعد الحصول على المشتقة الأولى.
مثلاً إذا كان لدينا الاقتران ص = ق(س) وكان هذا الاقتران قابل للاشتقاق فإن مشتقته الأولى هي: ص/ = دص/ دس = ق/(س) تمثل اقترانًا جديدًا، وإذا كان هذا الاقتران الجديد (المشتقة الأولى) قابلة للاشتقاق فإن مشتقتها تسمى المشتقة الثانية للاقتران الأصلي، ويُرمز لها بالرمز ص// أو ق//(س) أو د2ص/دس2 (وتُقرأ دال اثنين ص دال س تربيع)، وهكذا بالنسبة للمشتقات الأعلى الثالثة والرابعة. ونُعبر عن المشتقة من الرتبة ن بإحدى الصور الآتية:

فكر وناقش
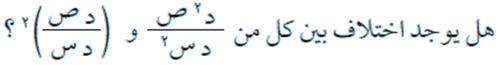
الحل
نعم هناك فرق بين المقدارين، لأن الأول هو المشتقة الثانية للاقتران ص أما الثاني فهو مربع المشتقة الأولى للاقتران ص.
مثال (12)
إذا كانت ق(س) = س 5 + 4 س 3 – 1 ، جد ق(5) (س) ثم جد ق(4) (2)
الحل
ق/(س) = 5 س 4 + 3 × 4 س 2 – صفر = 5 س 4 + 12 س 2
ق//(س) = 4 × 5 س 3 + 2 × 12 س = 20 س 3 + 24 س
ق(3) (س) = 3 × 20 س 2 + 24 = 60 س 2 + 24
ق(4) (س) = 2 × 60 س + صفر = 120 س
ق (5) (س) = 120
بالتعويض عن س = 2، يكون: ق(4) (2) = 120 × 2 = 240.
نشاط 4
إذا كان ق(س) كثير حدود، وكان ق(س) + ق//(س) = ٢ س٣ – ٣ س، فلإيجاد ق(1) نجد أولًا قاعدة ق(س). نلاحظ أن ق(س) اقتران كثير حدود من الدرجة الثالثة لأنه يحتوي على س3، وبالتالي تكون الصورة العامة له هي:
ق(س) = أ س٣ + ب س٢ + ج س + د
الحل
والتكملة تكون كما يلي بأخذ المشتقة الأولى ثم المشتقة الثانية:
ق/(س) = 3 أ س2 + 2 ب س + ج
ق//(س) = 6 أ س + 2 ب
والآن لدينا من المعطيات:
ق(س) + ق//(س) = ٢ س٣ – ٣ س
بالتعويض عن ق//(س) = 6 أ س + 2 ب ينتج أن:
ق(س) + 6 أ س + 2 ب = ٢ س٣ – ٣ س
ق(س) = ٢ س٣ – ٣ س – 6 أ س – 2 ب
ق(س) = ٢ س٣ – (٣ + 6أ) س – 2 ب
ق/(س) = 6 س2 – 3 – 6 أ
ق//(س) = 12 س
أ = 2، ب = صفر، جـ = – 15، د = صفر.
ق(س) = 2 س٣ – 15 س
ق/(س) = 6 س2 – 15
ق/(1) = 6 × 1 2 – 15 = – 9
مثال (13)
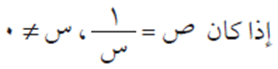
أثبت أن:
س٢ ص// + س ص/ = ص
الحل
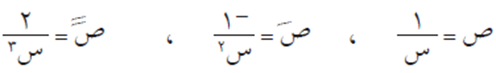
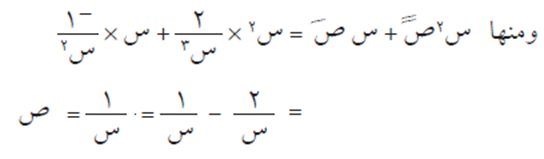
وهو المطلوب إثباته.
حلول تمارين الكتاب على درس قواعد الاشتقاق
السؤال الأول
جد ق/(س) في كل مما يأتي عند قيم س إزاء كلّ منها:
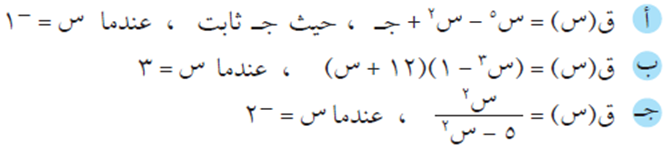
الحل
- ق/(س) = 5 س4 – 2 س ومنها يكون ق/(-1) = 5 × (-1)4 – 2 × (-1) = 5 + 2 = 7.
- ق/(س) = (س3 -1) × 1 + 3 س2 × (12 + س) = (س3 -1) + 36 س2 + 3 س3 = 4 س3 + 36 س – 1، ومنها ق/(3) = 4 × 27 + 36 × 9 – 1 = 431.
- ق/(س) = ](5 – س2) × 2 س – س2 × (5 – 2 س)[ ÷ (5 – س2)2 ، ومنها ق/(-2) = – 20.
السؤال الثاني
بالاعتماد على المعطيات في الجدول المجاور، جد ما يأتي:

الحل
أ. (ق + ه2)/(س) = ق/(س) + (ه(س) × ه(س))/ = ق/(س) + (ه(س) × ه/(س) + ه/(س) × ه(س)) = ق/(س) + 2 ه(س) × ه/(س) ومنها يكون = ق/(1) + 2 ه(1) × ه/(1) = 3 + 2 × -1 × -3 = 9.
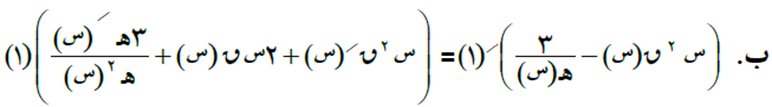
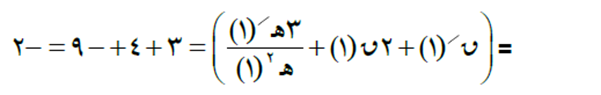
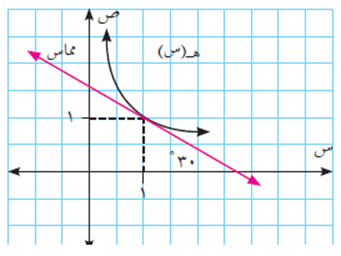
السؤال الثالث
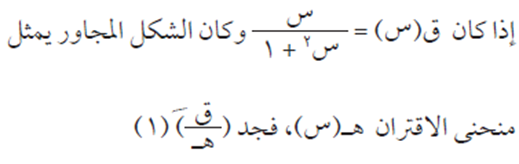
الحل
من قاعدة مشتقة حاصل قسمة اقترانين يكون:
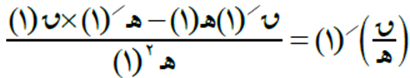
بالتعويض المباشر نحصل على ق(1) = 1/2.
والمشتقة ق/(س) = (المقام × مشتقة البسط – البسط × مشتقة المقام) / المقام تربيع، أي أن:
ق/(س) = ((س2+1)×1 – (س ×2س))/(س2+1)2 وبالتعويض عن س = 1 ينتج أن ق/(1) = صفر.
من التعريف، ميل المماس للمنحنى ه(س) يساوي ظل الزاوية التي يصنعها المماس مع الاتجاه الموجب لمحور السينات، أي أن:
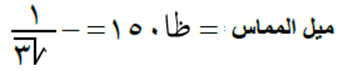
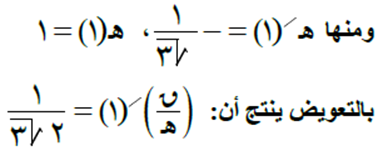
السؤال الرابع
الحل
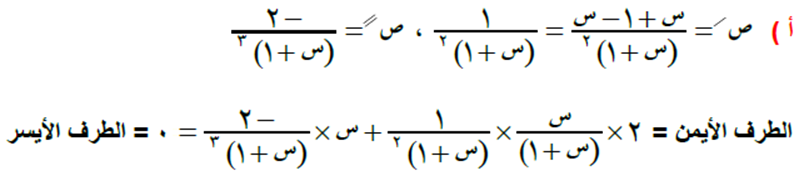
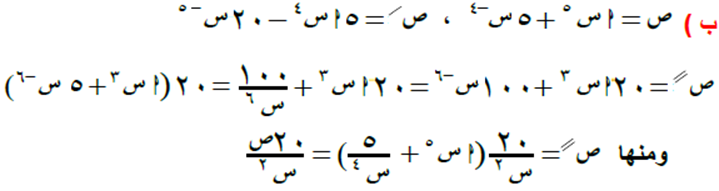
السؤال الخامس
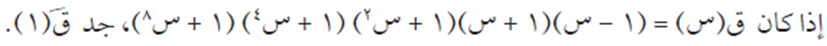
الحل
نقوم أولًا بإجراء التحليل والتبسيط للمقدار، بداية من أول قوسين الذين يمثلان فرق بين مربعين:
ق(س) = (1 – س2) (1 + س2) (1 + س4) (1 + س8)
ثم من حاصل ضرب أول قوسين مرة أخرى بنفس الطريقة يشكلان فرق بين مربعين، فيكون:
ق(س) = (1 – س4) (1 + س4) (1 + س8)
وبنفس الطريقة نحصل على:
ق(س) = (1 – س8) (1 + س8) = (1 – س16)
ومنها يكون: ق/(س) = – 16 س 15
بالتعويض يكون: ق/(1) = – 16.
السؤال السادس
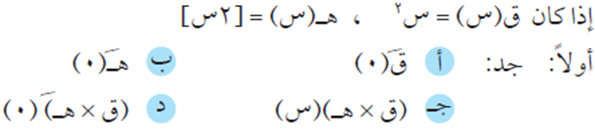
هل هذا يتناقض مع قاعدة مشتقة حاصل ضرب اقترانيين؟ فسّر إجابتك.
الحل
أولًا:
- بما أن ق(س) = س2، إذن ق/(س) = 2 س ومنها ق/(0) = صفر.
- ه/(س) = غير موجودة لأن الاقتران ه(س) غير متصل عندها.
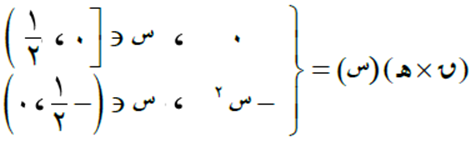
مع ملاحظة أن الاقتران الناتج متصل عند س = صفر.
- بالنسبة للمطلوب الأخير، لا يمكن حساب (ق × ه)/(س) بحسب قاعدة مشتقة حاصل ضرب اقترانين، وذلك لأن المشتقة ه/(س) غير موجودة. ولكن من تعريف هذا الاقتران أعلاه يكون لدينا:
ومنها يكون: (ق × ه)/(صفر) = صفر
ثانيًا: نستنتج أنه لا يمكن الحكم على وجود أو عدم وجود المشتقة باستخدام قواعد الاشتقاق لذلك نعود إلى إيجاد قاعدة الاقتران الأصلي ثم نحدد وهذا لا يتناقض مع القاعدة المذكورة.
السؤال السابع
إذا كان ق(س) = س٤ + أ س٣ – ٣، جد قيمة أ، حيث ق3(2) = 18.
الحل
ق/(س) = 4 س3 + 3 أ س2
ق//(س) = 12 س2 + 6 أ س
ق3(س) = 24 س + 6 أ
بالتعويض عن س = 2، نحصل على:
ق3(2) = 24 × 2 + 6 أ = 18 ومنها تكون أ = – 5
السؤال الثامن
إذا كان ق(س) = س ن، ن ϶ ص، وكان ق(٣)(س) = أ س، جد قيمة أ.
الحل
ق(س) = س ن
ق/(س) = ن س ن-1
ق//(س) = ن × (ن – 1) × س ن-2
ق3(س) = ن × (ن – 1) × (ن – 2) × س ن-3 = أ س
والآن بالنظر إلى المعادلة التالية:
ن × (ن – 1) × (ن – 2) × س ن-3 = أ س 1
نلاحظ أنه من تساوي الطرفين ومن قواعد الأسس: إذا تساوت الأساسات تتساوى الأسس، أي أن:
قوة س في الطرف الأيمن تساوي قوة س في الطرف الأيسر، أي أن: ن – 3 = 1 ومنها ن = 4.
كما أن: معامل س في الطرف الأيمن يساوي معامل س في الطرف الأيسر، أي أن:
ن × (ن – 1) × (ن – 2) = أ، ومنها ينتج أن أ = 24.





