2. العمليات على الأعداد المركبة

العمليات على الأعداد المركبة #

الأعداد المركبة مقادير جبرية #

بما أن العدد المركب هو مقدار جبري يُكتب على الصورة س + ص ت فإنه يمكن تعريف الجمع والضرب على الأعداد المركبة، من خلال عملية جمع وضرب مقدارين جبريين، ويكون لهما نفس خصائص عمليتي الجمع والضرب للمقادير الجبرية، مع مراعاة خصائص قوى ت.

تساوي عددين مركبين #

يتساوى العددان المركبان ع_١ = س_١ + ص_١ ت ، ع_٢ = س_٢ + ص_٢ ت إذا وفقط إذا كان لهما الجزء الحقيقي نفسه، والجزء التخيلي نفسه، أي أن يكون: س_١ = س_٢ ، ص_١ = ص_٢.

جمع وطرح الأعداد المركبة #

إذا كان ع _١ = س _١ + ص _١ ت ، ع _٢ = س _٢ + ص _٢ ت

فإن ع _١ ± ع _٢ = (س _١ ± س _٢) + (ص _١ ± ص _٢) ت

خصائص عملية الجمع على الأعداد المركبة #

• عملية الجمع عملية مغلقة: أي أنه Ɐ ع _١ ، ع _٢ ϶ ك فإن ع _١ + ع _٢ ϶  ك.
• عملية الجمع عملية تجميعية: أي أنه Ɐ ع_١، ع_٢، ع_٣ ϶ ك فإن (ع_١+ع _٢) + ع_٣ = ع١ + (ع٢+ع٣(.
• العنصر المحايد بالنسبة لعملية الجمع هو الصفر، حيث Ɐ ع ϶ ك، ٠ + ع = ع + ٠ = ع.
• لكل عنصر نظير جمعي: إذا كان ع ϶ ك فإن -ع ϶ ك، ويكون ع + (-ع) = (-ع) + ع = صفر. ويسمى -ع النظير الجمعي للعدد ع.
• عملية الجمع عملية تبديلية: Ɐ ع _١، ع _٢ ϶ ك، يكون: ع _١ + ع _٢ = ع _٢ + ع _١.

ضرب الأعداد المركبة #

إذا كان ع _١ = س _١ + ص _١ ت، ع _٢ = س _٢ + ص _٢ ت، س _١، س _٢، ص _١، ص _٢ ϶ ح.

فإن ع _١ ع _٢ = (س _١ س _٢ – ص _١ ص _٢) + (س _١ ص _٢ + س _٢ ص _١) ت

نتيجة (الضرب في عدد ثابت) #

إذا كانت جـ ϶ ح فإن ج (س + ص ت) = جـ س + جـ ص ت

مثال (1) #

ليكن ع _١ = ٣ + ٥ ت، ع _٢ = ٦ – ٥ ت فجد قيمة كل مما يأتي:

1. ٥ ع _١
2. ٣ ع _٢ + ٥ ع _١ – ٢ ت
3. ٣ م ، حيث ٤ – ت ع _١ = م (ت – ٣)، م ϶ ح

الحل

1. 5 ع _١ =  5 (3 + 5 ت) =  15 + 25 ت
2. ٣ ع _٢ + ٥ ع _١ – ٢ ت = 3 (6 – 5 ت) + 5 (3 + 5 ت) – 2 ت =  33 + 8 ت
3. ٤ – ت ع _١ = ٤ – ت (٣ + ٥ ت) = ٤ – ٣ ت – ٥ ت ^٢ = ٩ – ٣ ت = م (ت – ٣)، أي أن ٩ – ٣ت = – ٣ م + م ت، ومنها م = – ٣.

خصائص عملية الضرب على الأعداد المركبة #

• عملية الضرب مغلقة: لكل ع _١ ، ع _٢ ϶ ك، ع × _١ ع _٢ ϶ ك.
• عملية الضرب تجميعية: لكل ع _١، ع _٢، ع _٣ ϶  ك، (ع ₁ × ع _٢ ) × ع _٣ = ع ₁ × (ع _٢ × ع _٣(
• العنصر المحايد لعملية الضرب هو العدد 1، حيث لكل ع ϶ ك يكون ع × ١ = ١ × ع = ع.
• النظير الضربي: لكل ع ϶ ك، ع ≠ صفر، يوجد 1/ع ϶  ك بحيث 1/ع × ع = ع × 1/ع = ١. ويسمى 1/ع النظير الضربي للعدد ع ونرمز له بالرمز ع ^{– ١}.
• عملية الضرب تبديلية: لكل ع _١، ع _٢ ϶  ك، ع ₁ × ع _٢ = ع ₂ × ع ₁.

تعريف النظير الضربي للعدد المركب #

النظير الضربي للعدد المركب (س + ص ت) هو:

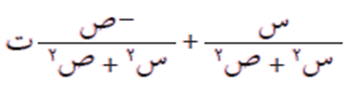
مثال (2)

جد النظير الضربي للعدد المركب ع = ١ + 2 (جذر2) ت

الحل

باستخدام القاعدة السابقة، حيث س = ١، ص = 2 (جذر 2)، وينتج أن: