2. الاقترانات المتزايدة والمتناقصة

2. الاقترانات المتزايدة والمتناقصة #

تعريف التزايد والتناقص #

يكون منحنى الاقتران ق(س) المعرّف في الفترة [أ ، ب]، لكل س_١، س_٢ ϶ [أ ، ب]:

1. متزايدًا في الفترة [أ ، ب] إذا تحقق الشرط: عندما س_١ > س_٢ فإن ق(س_١) > ق(س٢(
2. متناقصًا في الفترة [أ ، ب] إذا تحقق الشرط: عندما س_١ > س_٢ فإن ق(س_١) < ق(س_٢(
3. ثابتًا في الفترة [أ ، ب] إذا تحقق الشرط: عندما س_١ > س_٢ فإن ق(س₁) = ق(س_٢(

مثال (1) #

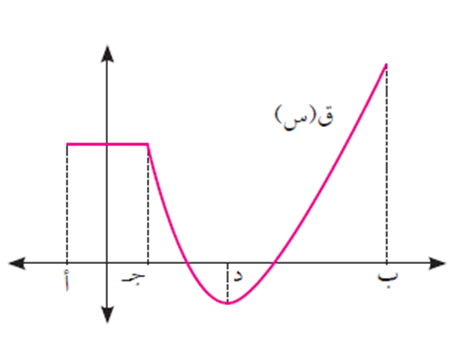
في الشكل التالي، حدد الفترات التي يكون فيها منحنى الاقتران ق(س) متزايدًا، أو متناقصًا، أو ثابتًا.

الحل

يكون منحنى الاقتران ق(س) ثابتًا في الفترة [أ ، جـ]، ويكون متناقصًا في الفترة [جـ، د]، لأنه كلما زادت قيمة س في الفترة [جـ، د] تقل قيمة ق(س)، ويكون متزايدًا في الفترة [دـ، ب] لأنه كلما زادت قيمة س في الفترة [دـ، ب] تزيد قيمة ق(س).

ملاحظة: لا يُطلب من الطالب التحقق من التزايد والتناقص جبريًا باستخدام التعريف.

التزايد والتناقص باستخدام اختبار المشتقة الأولى #

نظرية:

إذا كان ق(س) اقتران متصل في الفترة [أ، ب] وقابلًا للاشتقاق في الفترة ]أ، ب[ فإن منحنى:

1. الاقتران ق(س) يكون متزايدًا في القترة [أ، ب] إذا كانت قَ(س) < صفر، ⩝ س ϶ ]أ، ب[
2. الاقتران ق(س) يكون متناقصا في القترة [أ، ب] إذا كانت قَ(س) > صفر، ⩝ س ϶ ]أ، ب[
3. الاقتران ق(س) يكون ثابتا في القترة [أ، ب] إذا كانت قَ(س) = صفر، ⩝ س ϶ ]أ، ب[

مثال (2) #

جد فترات التزايد والتناقص لمنحنى الاقتران ق(س) علمًا بأن: ق^/(س) = (س² – ١)(س + 2)، س ϶ ح.

الحل

نضع ق^/(س) = صفر، ومنها يكون: (س² – 1)(س + 2) = صفر

ومنها (س – 1)(س + 1)(س + 2) = صفر

وينتج أن: س = 1 أو س = – 1 أو س = – 2

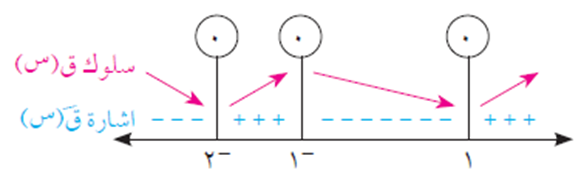
من إشارة ق^/(س) في الشكل أعلاه، يكون:

منحنى ق(س) متناقصًا في الفترة ]-∞، -2] ، [- 1، 1]، ومتزايدًا في الفترة [- 2، -1]، [1، ∞[.