1. التجزئة ومجموع ريمان

التجزئة ومجموع ريمان #

تعريف التجزئة النونية #

إذا كانت [أ ، ب] فترة مغلقة، وكانت: Ơ_ن = {أ = س₀، س_١، س _٢، س_٣، … ، س _ن = ب} حيث:

س₀ > س_١ > س _٢ > س_٣ ….. > س _ن، فإننا نسمي ن تجزئة نونية للفترة [أ ، ب].

وتسمى الفترة [س _{ر- ١}، س _ر] الفترة الجزئية الرائية، وطولها دلتا ∆ س _ر = س _ر – س _ر-١

طول الفترة الكلية = مجموع أطوال جميع الفترات الجزئية، أي أن بالرموز:

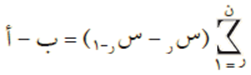
ملاحظة #

من التعريف، يتضح أنه لكتابة أي تجزئة ن لفترة ما يجب أن تكون:

1. الفترة مغلقة
2. تبدأ التجزئة من بداية الفترة وتنتهي بنهايتها
3. عناصر التجزئة مرتبة ترتيبًا تصاعديًا

مثال (1) #

أي من الآتية يعتبر تجزئة للفترة [-1 ، 3]

1. Ơ ₄ = }-1، 1، 3/2، 2، 3{
2. Ơ ₄ = }0، 1، 3/2، 2، 3{
3. Ơ ₄ = }-1، 1، 2، 3، 4{
4. Ơ ₄ = }-1، 1، 0، 2، 3{

الحل

تعريف التجزئة النونية المنتظمة #

تسمى التجزئة ن تجزئة نونية منتظمة للفترة [أ، ب]، إذا كانت أطوال جميع الفترات الناتجة عنها متساوية، ويكون فيها طول الفترة الجزئية = طول الفترة الكلية / عدد الفترات الجزئية = (ب – أ) / ن.

مثال (2) #

اكتب تجزئة خماسية منتظمة للفترة [-2، 13].

الحل

طول الفترة الجزئية = (ب – أ) / ن = (13 – (-2)) / 5 = 3

ومنها تكون {Ơ ₄ = {-2، 1, 4, 7, 10, 13

ملاحظة #

يتم تطبيق قواعد وحسابات المتتاليات الحسابية بنقس الطريقة على عناصر التجزئة، بحيث يكون الحد الأول في المتتالية هو أ والحد الأخير فيها هو ب، والمسافة بين كل عنصر والذي يليه هو أساس المتتالية.

تعريف

إذا كان ق(س) اقترانًا معرفًا في الفترة [أ، ب]، وكانت  Ơ_ن تجزئة نونية للفترة ]أ، ب[، فإن المقدار:

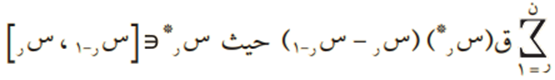
يسمى مجموع ريمان، ويُرمز له بالرمز  م (Ơ_ن ، ق).

وإذا كانت التجزئة نونية منتظمة فإن:

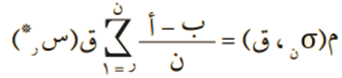
مثال (3) #

إذا كان ق(س) = س – ٢، وكانت {Ơ ₃ = {3، 4، 5، 6 تجزئة ثلاثية للفترة [3، 6]، فاحسب م (Ơ ₃، ق)، معتبرًا س _ر * = س _ر-1

الحل

نكوّن الجدول التالي:

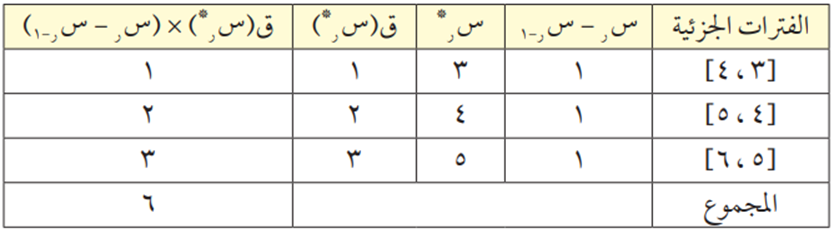
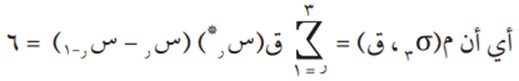
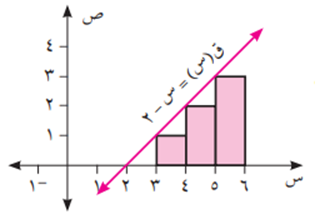
من الشكل أعلاه نلاحظ أن مجموع مساحات المستطيلات يساوي م (Ơ ₃، ق) = 6.