تطبيقات التكامل غير المحدود
أولًا: تطبيقات هندسية
يمكن تطبيق قواعد التكامل غير المحدود في حل مسائل الهندسة، ويتضح ذلك من المثال التالي.
مثال (1)
إذا كان المستقيم ص = س + ٢ يمس منحنى الاقتران ق(س) عند س = صفر، وكان ق//(س) = ٦ س، جد قاعدة الاقتران ق(س).
الحل
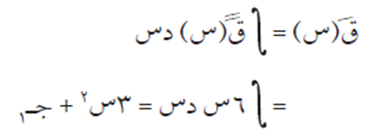
لكن ق/(صفر) = ١
ومنها جـ1 = 1
ق(س) = ٣ س٢ + 1
وأيضًا:
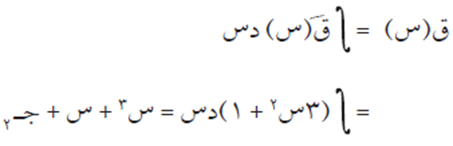
وبما أن النقطة (0، 2) هي نقطة تماس، فإن ق(0) = ٢، ومنها جـ ٢ = ٢، ويكون:
ق(س) = س٣ + س + ٢
ثانيًا: تطبيقات فيزيائية
تأمل المخطط الآتي، ولاحظ العلاقة بين المسافة ف بدلالة الزمن: ف(ن) والسرعة ع بدلالة الزمن: ع(ن) والتسارع ت بدلالة الزمن: ت(ن) في كل من التفاضل والتكامل.
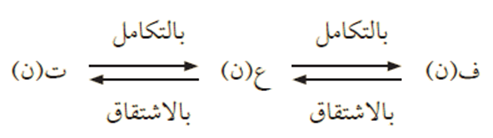
مثال (2)
بدأ جسم التحرك في خط مستقيم من نقطة الأصل ومبتعدًا عنها، فإذا كانت سرعته في أي لحظة تُعطى بالعلاقة ع(ن) = ٣ ن٢ + ٢ ن، فما بُعد الجسم عن نقطة الأصل بعد ثانيتين من بدء الحركة؟
الحل
ع(ن) = ٣ ن٢ + ٢ ن
وبما أن ف(صقر) = صفر (لأن الجسم بدأ الحركة من السكون)، فإن الثابت جـ = صفر.
أي أن ف(ن) = ن٣ + ن٢
بًعد الجسم عن نقطة الأصل بعد ثانيتين = ف(2) = ١٢ متر.





