التكامل غير المحدود
تعريف معكوس المشتقة
إذا كان الاقتران ق(س) متصلًا في الفترة [أ ، ب] فإن م(س) يسمى معكوس المشتقة (اقتران أصلي) للاقتران ق(س) إذا كان م/(س) = ق(س)، لكل س ϶ ]أ ، ب[.
مثال (1)
تحقق من أن الاقتران م(س) = 1/4 س4 هو اقتران أصلي للاقتران ق(س) = س3
الحل
الاقتران م(س) = 1/4 س4 هو اقتران أصلي للاقتران ق(س) = س3 لأن مشتقة الاقتران م/(س) = 4 × 1/4 س3 = س3 = ق(س).
كما أن ق(س) متصل لأنه كثير حدود.
قاعدة
إذا كان م(س) اقترانًا أصليًا للاقتران ق(س) فإن م(س) + ج هي الصورة العامة لأي اقتران أصلي للاقتران ق(س) حيث جـ عدد ثابت.
نتيجة
الفرق بين أي اقترانين أصليين لاقتران معين يساوي اقترانًا ثابتًا دائمًا.
تعريف التكامل فير المحدود
- تسمى مجموعة كل الاقترانات الأصلية للاقتران ق(س) بالتكامل غير المحدود للاقتران ق(س) بالنسبة لـ س ويُرمز له بالرمز:
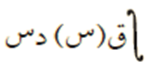
ويُقرأ: تكامل ق(س( دال س.
- إذا كان م/(س) = ق(س) فإن:
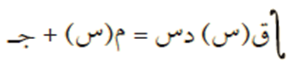
حيث جـ عدد ثابت يسمى ثابت التكامل.
- إذا كان ق(س) اقترانًا متصلًا فإن:
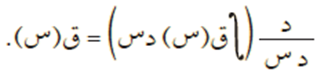
مثال (2)
إذا كان ق(س) اقترانًا متصلًا فجد ق(٢)، ق/(2) إذا كان:
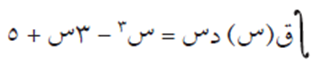
الحل
بما أن ق(س) اقتران متصل، إذن:
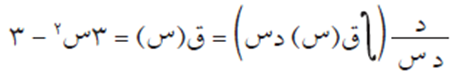
ومنها ق(2) = 3 × 2 2 – 3 = 9
ق/(س) = 6 س
ومنها ق/(2) = 12





