5. حل أنظمة المعادلات الخطية باستخدام المصفوفات

حل أنظمة المعادلات الخطية باستخدام المصفوفات #

أولًا: حل المعادلات بطريقة النظير الضربي #

يمكننا تمثيل نظام من المعادلات الخطية على شكل معادلة مصفوفية، باستخدام ثلاث مصفوفات، هي: مصفوفة المعاملات أ، ومصفوفة المتغيرات ك، ومصفوفة الثوابت جـ.

مثلًا، إذا كان لدينا نظام المعادلات الخطّيّة الآتي:

2 س + 3 ص = 10

– 3 س + 5 ص = 4

فإن مصفوفة المعاملات هي:

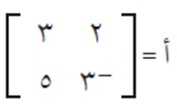
ومصفوفة المتغيرات هي:

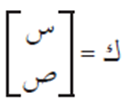
ومصفوفة الثوابت هي:

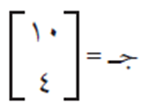
ويمثل النظام السابق من المعادلات الخطية بمعادلةٍ مصفوفيةٍ على الصورة أ × ك = ج كما يلي:

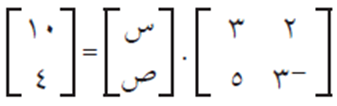
مصفوفة المعاملات × مصفوفة المتغيرات = مصفوفة الثوابت

وتكون ك = أ ^{– ١} × جـ ، بشرط أن تكون المصفوفة أ غير منفردة، حتى يمون لها نظير ضربي.

مثال (1) #

حل نظام المعادلات التالي بطريقة النظير الضربي:

2 س + ص = – 1

4 س + ص = 1

الحل

نكتب المعادلات على شكل معادلة مصقوقية كما يلي:

مصفوفة المعاملات × مصفوفة المتغيرات = مصفوفة الثوابت

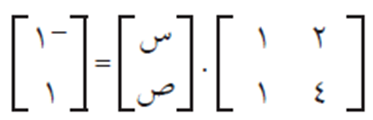
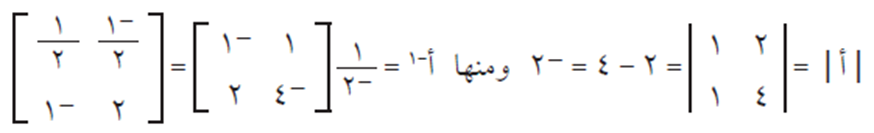
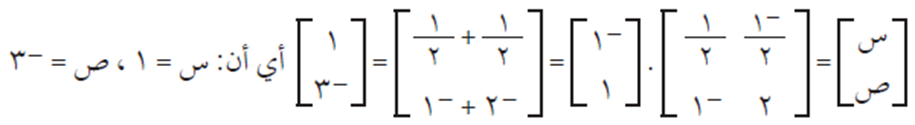
ثانيًا: حل نظام المعادلات بطريقة كريمر #

سبق وأن مثلنا أي نظام من المعادلات الخطّيّة بمعادلةٍ مصفوفيةٍ على النحو أ × ك = جـ، حيث إن مصفوفة المعاملات أ غير منفردةٍ، ك مصفوفة المتغيرات، جـ مصفوفة الثوابت. فإذا كان النظام يتضمن المتغيرين س، ص، فإننا قيمتهما تكون كما يلي:

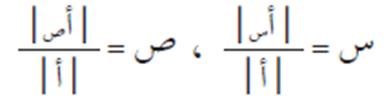
حيث أن:

المصفوفة أ _س هي المصفوفة الناتجة من استبدال عمود معاملات س بعمود الثوابت.

المصفوفة أ _ص هي المصفوفة الناتجة من استبدال عمود معاملات ص بعمود الثوابت.

مثال (2) #

باستخدام طريقة كريمر حل نظام المعادلات الآتي:

3 س + 5 ص = 1

2 س + 3 ص = صفر

الحل

نقوم أولًا بتكوين المصفوفات الثلاثة كما يلي:

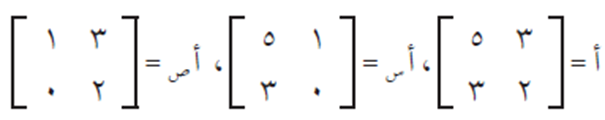
ثم نقوم بإيجاد كل من:

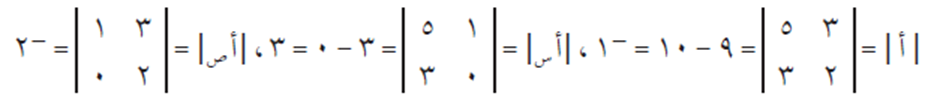
ثم نحسب قيمة س، ص حسب التعريف كما يلي:

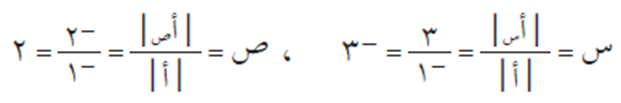
ثالثًا: حل نظام المعادلات بطريقة جاوس #

طريقة عالم الرياضيات الألماني كارل جاوس، وهي الطريقة التي تعتمد على تكوين مصفوفة ممتدة (تشمل المعاملات والثوابت في نظام المعادلات)، فإذا كان لدينا نظام المعادلات التالي:

أ _١١ س + أ _٢١ ص + أ _٣١ ع = جـ _١

أ _١٢ س + أ _٢٢ ص + أ _٣٢ ع = جـ _٢

أ ₁₃ س + أ ₂₃ ص + أ _٣٣ ع = جـ _٣

فإن المصفوفة الممتدة لهذا النظام هي أ بار، حيث:

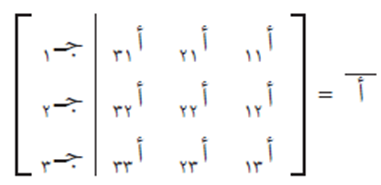
وللحصول على حل لنظام المعادلات، نجري بعض العمليات على صفوف المصفوفة أ، لنحصل على مصفوفةٍ مثلثية علوية ونجد منها أولًا قيمة المتغير ع، ثم بالتعويض العكسي نجد قيمة المتغير ص، ثم قيمة المتغير س.

والعمليات التي يمكن إجراؤها على صفوف المصفوفة أ هي كما يلي:

• تبديل صف مكان صف آخر.
• ضرب مدخلات أي صف بعدد لا يساوي صفر.
• ضرب مدخلات أي صف بعدد لا يساوي صفر، وإضافتها إلى صف آخر.

مع ملاحظة أنه إذا كانت أ ₁₁ = صفر، فيمكن تبديل صف مدخلته الأولى ≠ صقر مكان الصف الأول في المصفوفة الممتدة أ بار.

مثال (3) #

استخدم طريقة جاوس لحل نظام المعادلات:

3 س + 7 ص = 10

2 س – 5 ص = – 3

الحل

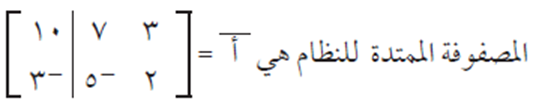
 ونقوم بإجراء العمليات على النحو الآتي:

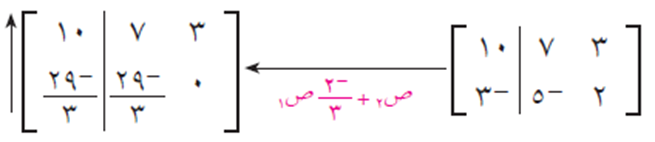
ومنها تكون:

-29/3 ص = -29/3 … أي أن ص = 1

وبالتعويض العكسي في المعادلة الأولى، نحصل على:

3 س + 7 × ١ = 10، ومنها س = 1

مثال (4) #

استخدم طريقة جاوس لحل نظام المعادلات التالي:

س + ص – ع = 9

ص + 3 ع = 3

– س – 2 ع = 2

الحل

نكون المصفوفة الممتدة أ بار:

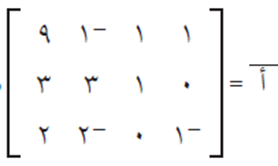
ونجري العمليات الآتية:

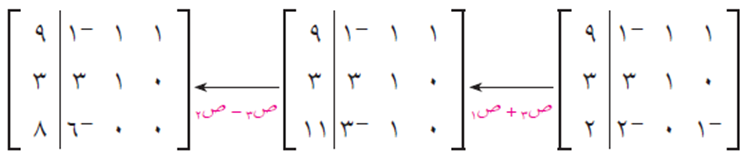
وبهذا حصلنا على مصفوفة مثلثية علوية، فنجد قيم المجاهيل بالتعويض العكسي، فيكون:

– 6 ع = 8 ، ومنها ع = -4/3

كذلك ص + 3 ع = 3، ومنها ص = 7

كما أن: س + ص – ع = 9 ومنها س = 2/3.