مفهوم تشابه واختلاف البيانات
في معظم تقنيات تحليل وتنقيب البيانات، مثل خوارزمية التحليل العنقودي وخوارزمية الجار الأقرب، تظهر الحاجة إلى قياس تشابه واختلاف البيانات من أجل تقييم مدى التشابه والاختلاف فيما بين البيانات. مثلا قد يحتاج أحد المراكز التجارية إلى تجزئة زبائنه إلى مجموعات ذات خصائص مميزة، كأن يقوم بتجميع الزبائن المتشابهين في الدخل أو العمر، بحيث يمكن استخدام هذه المعلومات في وضع خطط واستراتيجيات التسويق المختلفة التي تستهدف فئات وشرائح معينة من الجمهور.
ففي خوارزميات التحليل العنقودي يتم تصنيف البيانات وتقسيمها إلى فئات جزئية بحيث تنتمي العناصر المتشابهة لأحد الفئات وبقية العناصر التي تختلف عنها تنتمي للفئات الأخرى، وكذلك الأمر في خوارزمية الجار الأقرب فهي تبحث في التشابه بين العنصر المستكشف والعناصر الأقرب له، لذا فإنه يلزم معرفة تشابه البيانات من أجل تلك الأغراض.
مثلا في أحد الخوارزميات التي تستكشف أنواع الأمراض وتشخيصها قد يتم اللجوء لبحث التشابه في الأعراض التي تظهر على أحد المرضى مع الأعراض التي تظهر على مرضى آخرين مصابين بالفعل بمرض معين، بحيث يتم استنتاج إصابته بنفس المرض، أو حتى استعداده للإصابة به، في حال وجود تشابه بالفعل بينه وبين المرضى الآخرين في سمات معينة، وبالتالي التوصل إلى التشخيص الصحيح لحالة المريض.
في هذا القسم سوف نتطرق لطرق قياس التشابه والاختلاف بين البيانات باستخدام أساليب تقريبية.
المحتويات
مقياس تشابه واختلاف البيانات
إن مقياسي التشابه والاختلاف بين البيانات مرتبطان ببعضهما البعض. ومقياس تشابه عنصرين أ، ب يكون مساويًا للصفر، إذا لم يكن بينهما أي تشابه، فكلما زادت هذه القيمة يزداد التشابه بينهما وحتى الوصول إلى درجة التطابق عندما تصل هذه القيمة إلى الواحد الصحيح =1.
أما قياس الاختلاف بين عنصرين أ، ب، فيعمل بطريقة عكسية، فهو يبدأ بقيمة تساوي الصفر إذا كان العنصرين متشابهين لدرجة التطابق، وكلما زاد الاختلاف بينهما يزداد قياس الاختلاف حتى يصل لقيمة الوحد الصحيح، عندما يكونا مختلفين تماماً.
ويمكن الربط بين قيمة القياسين بالمعادلة الرياضية التالية:
طريقة قياس تشابه واختلاف البيانات
يمكن قياس التشابه أو الاختلاف بين البيانات بأنواعها المختلفة، وأسهلها عندما تكون البيانات من النوع الرقمي.
ويتم التعبير عن التشابه والاختلاف بطرق مختلفة، مثلا يمكن قياس التشابه بين أعمار مجموعة من طلاب المدارس ومجموعة أخرى من طلاب الجامعات، وبذلك تكون المقارنة من النوع الرقمي البحت التي يمكن التعبير عنها بسهولة باستخدام مقاييس التحليل الإحصائي مثل مقاييس النزعة المركزية، كالوسيط والمتوسط الحسابي مثلاً، ومع ذلك فهناك طرق أخرى لقياس التشابه والاختلاف بين البيانات الرقمية سيتم التطرق إليها في هذا الفصل.
أما قياس تشابه واختلاف البيانات من النوع الاسمي تكون من خلال معرفة عدد الخصائص أو السمات المشتركة فيما بينها وعدد السمات غير المشتركة.
تشابه واختلاف البيانات من النوع الاسمي
يمكن قياس الاختلاف بين البيانات الاسمية من خلال المعادلة الرياضية التالية:
قياس الاختلاف = (العدد الإجمالي للسمات – عدد السمات المشتركة) / العدد الإجمالي للسمات
مثلاً، لو افترضنا أنه لدينا في إحدى قواعد البيانات الخاصة بمحل أو مركز تجاري السجلات التالية لزبونين أ، ب، حيث:
| الزبون | العمر | الدخل | المنطقة | عدد رحلات التسوق | حجم المشتريات |
| أ | مسن | مرتفع | س | متوسط | متوسط |
| ب | شاب | متوسط | س | متوسط | متوسط |
باعتبار أن جميع البيانات الواردة في الجدول هي من النوع الاسمي، يمكن حساب الاختلاف بين الزبون أ، والزبون ب، ويكون:
قياس الاختلاف بين أ، ب = (إجمالي عدد السمات – عدد السمات التي يتشابهون بها) / إجمالي عدد السمات
= (5 – 3) / 5
= 2 / 5
أو:
= 0.4
وذلك باعتبار أن كل سمة من السمات الخمسة الواردة في الجدول هي سمة اسمية تميز الزبون عن غيره من الزبائن.
استخدام نظام الأوزان في قياس التشابه والاختلاف بين البيانات
يمكن تخصيص أوزان أثقل نسبيًا لبعض السمات حتى تكون مؤثرة بشكل أكبر في قياس التشابه، ففي المثال السابق يمكن مثلا تخصيص وزن مقداره (1) فقط لكل السمات باستثناء سمة العمر يتم تخصيص الوزن (2) لها، فيكون بالتالي إجمالي الوزن الكلي للسمات = 6 بدلا من 5، ثم يتم استخدام معادلة حساب الاختلاف التالية:
قياس الاختلاف بين أ، ب = (إجمالي الوزن الكلي للسمات – مجموع أوزان السمات التي يتشابهون بها) / إجمالي الوزن الكلي للسمات
وتكون النتيجة أن يصبح:
قياس الاختلاف بين أ، ب = (6 – 3) / 6
= 0.5
أي أن الاختلاف بين أ ، ب زاد عندما تم رفع الوزن النسبي الخاص بالسن أو العمر.
كما يمكن تخصيص أوزان متنوعة للسمات بحسب احتياجات الجهة التي تقوم بالتحليل والتنقيب، وبحسب ما تستشعره من أهمية لتلك السمات والنتائج التي ترغب بالتوصل إليها من دراستها وتحليلها.
قياس تشابه واختلاف البيانات المنطقية Boolean أو في النظام الثنائي Binary
يمكن قياس تشابه واختلاف البيانات المنطقية أو المستخدمة في النظام الثنائي، أي تلك التي تأخذ قيمتين فقط بشكل دائم (1 أو صفر)، وقد تكون تلك القيم مناظرة لقيم ذات معنى في قائمة البيانات التي يتم بحث اختلافها وتشابهها، كأن تكون القيم المناظرة لها هي قيم منطقية (نعم و لا)، أو قيم (موافق وغير موافق)، ويتم قياس التشابه والاختلاف بين هذا النوع من البيانات من خلال المعادلة التالية:
الاختلاف بين المتغير (أ) والمتغير (ب) = (س + ص) / (ل + س + ص + ع)
حيث:
س = عدد السمات التي تكون قيمتها (1) للمتغير (أ) وقيمتها (صفر) للمتغير (ب)
ص = عدد السمات التي قيمتها (صفر) للمتغير (أ) وقيمتها (1) للمتغير (ب)
ل = عدد السمات التي قيمتها (1) للمتغير (أ) وقيمتها (1) للمتغير (ب)
ع = عدد السمات التي قيمتها (صفر) للمتغير (أ) وقيمتها (صفر) للمتغير (ب)
مع ملاحظة أن إجمالي عدد السمات هو (ن)، حيث:
ن = ل + س + ص + ع
إهمال السمات السلبية
ومن المتعارف عليه في بعض مجالات بحوث تشابه واختلاف البيانات من النوع المنطقي أو الثنائي أن يتم إهمال عدد السمات السلبية المشتركة (ع)، أي عدد السمات التي تأخذ القيمة (صفر) في كلا المتغيرين، وذلك باعتبار أنه ليس لها دلالة ذات تأثير حقيقي، في حين أنه لا يتم إهمال عدد السمات الإيجابية المشتركة (ل) أي عدد السمات التي قيمتها (1) في كلا المتغيرين، حيث يكون لهذا العدد دلالة ذات تأثير مهم لحساب الاختلاف بين البيانات.
ويظهر هذا الأمر بشكل واضح في الاختبارات الطبية التي تتم على المرضى والهادفة لاستكشاف استجابتهم لأنواع مختلفة من الأدوية أو العقاقير المخصصة للعلاج، حيث أن عدم الاستجابة من جميع المرضى هو أمر يتم إهماله واستبعاده من دراسة الاختلاف فيما بينهم ولا يغير من درجة تقييم فاعلية الدواء الذي يتم دراسته.
وبذلك تصبح المعادلة الخاصة بحساب الاختلاف بين البيانات الأكثر شيوعًا في البيانات المنطقية وبيانات النظام الثنائي كما يلي:
الاختلاف بين المتغير (أ) والمتغير (ب) = (س + ص) / (ل + س + ص)
مثال تطبيقي
نفرض أنه لدينا جدول السجلات التالية، والخاصة بمجموعة من المرضى في أحد المراكز الطبية، والذي يبين الإصابة بأعراض الحمى والسعال ونتائج أربعة اختبارات طبية محددة بقيمتين وهما القيمة (1) المناظرة للنتيجة الإيجابية (بالإنجليزية: Positive)، والقيمة (صفر) المناظرة للنتيجة السلبية (بالإنجليزية: Negative)، والجدول كما يلي:
| المريض | الجنس | حمى | سعال | اختبار1 | اختبار2 | اختبار3 | اختبار4 |
| أ | ذكر | نعم | لا | 1 | صفر | صفر | 0 |
| ب | أنثى | نعم | نعم | صفر | صفر | 0 | 0 |
| ج | ذكر | نعم | لا | 1 | صفر | 1 | 0 |
| …. |
وبفرض أن حساب الاختلاف بين المرضى سوف يتم باستخدام الطريقة الثانية، التي يتم فيها إهمال السمات المشتركة ذات القيم السلبية حيث أنها تكون غير مهمة من المنظور الطبي، فإنه يكون:
الاختلاف بين المريض (أ) والمريض (ب) = (س + ص) / (ل + س + ص)
= (1 + 1) / (1 + 1 + 1)
أو:
= 0.67
الاختلاف بين المريض (أ) والمريض (ج) = (س + ص) / (ل + س + ص)
= (0 + 1) / (2 + 0 + 1)
أو:
= 0.33
والاختلاف بين المريض (ب) والمريض (ج) = (س + ص) / (ل + س + ص)
= (1 + 2) / (1 + 1 + 2)
أو:
= 0.75
ويتضح من النتائج أعلاه أن المريض (ب) والمريض (ج) هما الأكثر اختلافًا، وبالتالي يكون احتمال إصابتهم بنفس المرض هو احتمال ضعيف، ومن بين المرضى الثلاثة فإن المريض (أ) والمريض (ج) هما الأكثر تشابهًا وبالتالي هما الأكثر احتمالا بأن يُصابوا بنفس المرض.
قياس تشابه واختلاف بيانات النوع الرقمي
يمكن قياس تشابه واختلاف البيانات من النوع الرقمي (بالإنجليزية: Numerical Attributes) باستخدام معادلة المسافة الإقليدية، وهي المعادلة التي تحسب المسافة بين نقطتين في الفراغ متعدد الأبعاد والمنسوبة للعالم “إقليدس”، والتي يتم التعبير عنها رياضيًا كما يلي:
المسافة بين النقطتين (أ) و (ب) = الجذر التربيعي لـ [(س أ – س ب)2 + (ص أ – ص ب)2 + (ع أ– ع ب)2 + …..]
حيث أن كل من السجلات أ، ب يتم التعبير عنها باستخدام الخصائص أو السمات س، ص، ع، …..، أي أن:
أ = (س أ، ص أ، ع أ، ……)
ب = (س ب، ص ب، ع ب، ……)
وحتى يتم قياس التشابه والاختلاف بين البيانات الرقمية فإنه يلزم تحويلها أولا إلى قيم ضمن فترة محددة ما بين القيمتين (-1، +1)، أو بين القيمتين (صفر، 1) وذلك من أجل حساب مقدار التشابه أو الاختلاف فيما بينها بما يتناسب مع قيمة التشابه والاختلاف أصلا والتي تقع ضمن تلك الحدود، ويتم ذلك باستخدام أسلوب التدريج الذي يناظر القيمة الحقيقية للبيانات، وسوف يتم التطرق لهذه الطرق بالتفصيل في القسم الخاص بتحضير البيانات للتحليل والتنقيب، ومع ذلك سيتم استخدام هذه الطريقة في المثال التطبيقي التالي.
مثال تطبيقي على تشابه البيانات الرقمية
نفرض أنه لدينا في قاعدة بيانات أحد الشركات التجارية سجلات بعض الزبائن كما يلي:
| الزبون | العمر | الدخل | المنطقة | حجم المشتريات |
| أ | 55 | 2000 | م | 400 |
| ب | 35 | 1000 | م | 600 |
ويمكن تمثيل بيانات كل من الدخل وحجم المشتريات للزبونين أ، ب بالرسم الديكارتي كما في الشكل التالي:
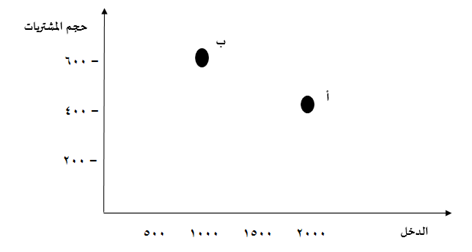
حيث يمثل المحور (س) قيمة الدخل، ويمثل المحور (ص) كمية أو حجم المشتريات.
والمطلوب حساب الاختلاف بين السجل (أ) والسجل (ب) من حيث الدخل وحجم المشتريات، وهي القيم الرقمية التي وردت في الجدول.
الحل
وتكون قيمة الاختلاف بين النقطتين (أ) ، (ب) من منظور هندسي هي المسافة التي تفصل بينهما على الرسم.
وحتى يمكن قياس الاختلاف بينهما من منظور نسبي تتراوح قيمته ما بين (صفر، 1) فإنه ينبغي أولا تحويل البيانات إلى قيم تقع بداخل الفترة المحددة (صفر ، 1 )، وذلك كما يلي:
بالنسبة لقيمة الدخل، فإن أعلى قيمة على التدريج = 2000، ولتكن هذه القيمة هي المناظرة للقيمة (1) على التدريج أو المقياس.
أما أصغر قيمة فتكون هي المناظرة للقيمة (صفر) على التدريج، ويمكن هنا اعتبار أن هذه القيمة هي التي تمثل الصفر الحقيقي فعلاً، فيكون بالتالي قيمة الدخل (1000) الواردة في الجدول تناظر القيمة (0.5) على التدريج، حيث أنها تقع في منتصف المسافة بين صفر و2000.
وبالمثل يمكن تحديد قيم حجم المشتريات لكل من الزبون (أ)، (ب) بحيث تكون أعلى قيمة لحجم المشتريات وهي (600) مناظرة للقيمة (1) على التدريج، وبالتالي تكون القيمة (400) مناظرة للقيمة (0.67) على التدريج.
ولحساب الاختلاف بين (أ) و (ب) فإنه يكون مساويًا للمسافة بين النقطتين (أ) و (ب) حيث يتم التعبير عنهما بقيمة كل من الدخل وحجم المشتريات على التدريج كما يلي:
أ = (1، 0.67)
ب = ( 0.5، 1)
ويكون بحسب معادلة حساب قيمة الاختلاف التي تساوي المسافة بينهما:
الاختلاف بين أ، ب = الجذر التربيعي لـ [(1 – 0.5)2 + (1 – 0.67)2]
= الجذر التربيعي لـ [( 0.5)2 + (0.33)2]
= 0.6
قياس تشابه واختلاف بيانات النوع الرتبي
يمكن قياس تشابه واختلاف البيانات من النوع الرتبي (بالإنجليزية: Ordinal Attributes)، وذلك باعتبار أن الترتيب فيها يكون له دلالة من حيث القيمة، مثلا كما يحدث في حالة ترتيب درجات الحرارة لمدينة ما بأنها تأخذ القيم التالية (منخفضة، متوسطة، مرتفعة). فبالرغم من عدم وجود قيمة رقمية لمثل تلك البيانات إلاّ أنها قابلة للترتيب تصاعديًا من الأصغر للأكبر أو تنازليًا من الأكبر للأصغر.
وحتى يتم قياس التشابه والاختلاف بين البيانات من النوع الرتبي فإنه يلزم تحويلها أولا إلى بيانات من النوع الرقمي تقع ضمن تدريج محدد في الفترة (صفر، 1)، أي بنفس الطريقة التي تم فيها تحويل البيانات الرقمية، والفرق في هذه الحالة أنه في حالة البيانات الرتبية يلزم أولا تحديد أوزان رقمية لكل قيمة من القيم حتى نستطيع أن نعطيها القيم المناظرة لها في التدريج على الفترة المحددة.
مثال توضيحي
في حالة درجات الحرارة، يمكن افتراض أن وحدات القياس المستخدمة هي الدرجة المئوية وأن القيم الحقيقية للدرجات كما يلي:
- المنخفضة: هي التي تتراوح بين صفر و 15 درجة مئوية
- المتوسطة: هي التي تتراوح بين 16 درجة و 30 درجة مئوية
- المرتفعة: هي التي تتراوح بين 31 درجة و 50 درجة مئوية
أما في الخطوة الثانية فيتم تحويل قيمة الدرجات إلى القيم المناظرة في التدريج. مثلا، لو افترضنا أن التدريج يبدأ بالقيمة (صفر) المناظرة للقيمة صفر درجة مئوية، وينتهي بالقيمة (1) المناظرة للقيمة (50) درجة مئوية، فتكون قيمة (30) درجة مئوية مناظرة للقيمة (0.6) على تدريج الفترة.
وفي الخطوة الأخيرة يتم حساب قيمة الاختلاف بين البيانات بنفس الطريقة التي تم اتباعها في حساب الاختلاف بين البيانات الرقمية، أي باستخدام معادلة المسافة الإقليدية بين نقطتين على الرسم الديكارتي، كما يلي:
الاختلاف بين المتغيرين (أ)، (ب) = المسافة بين النقطتين (أ) و (ب)
أي أن:
الاختلاف بين المتغيرين (أ)، (ب) = الجذر التربيعي لـ [( س1 – س2)2 + (ص1 – ص2)2]
حيث أن: أ = (س1، ص1)، ب = (س2، ص2)
قياس تشابه واختلاف النصوص
يتم قياس تشابه واختلاف بيانات النصوص (بالإنجليزية: Text Similarity) من خلال تحديد مجموعة من الكلمات الأساسية تُسمى الكلمات المفتاحية التي تظهر في تلك النصوص، والتي تُعتبر كلمات مميزة ولها دلالة معينة بالنسبة للهدف من المقارنة التي يجري تنفيذها، بعد ذلك تتم عملية إحصاء لعدد مرات تكرار ظهور تلك الكلمات في كل نص من النصوص التي يتم مقارنتها وبحث تشابهها واختلافها، ثم توضع النتائج في جدول مخصص كالمبين أدناه، وهو جدول يوضح عدد تكرار مجموعة من الكلمات المفتاحية في أربعة بحوث متخصصة في تطوير التعليم بهدف استكشاف التشابه والاختلاف فيما بينها:
جدول التكرار
| البحث | الكلمات المفتاحية | |||||||||
| بحث | علوم | تربية | تعليم | تنمية | تطوير | تحديث | إبتكار | إبداع | تقدم | |
| بحث (أ) | 5 | 0 | 3 | 0 | 2 | 0 | 0 | 2 | 0 | 0 |
| بحث (ب) | 3 | 0 | 2 | 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| بحث (ج) | 0 | 7 | 0 | 2 | 1 | 0 | 2 | 3 | 0 | 0 |
| بحث (د) | 0 | 1 | 0 | 0 | 1 | 2 | 0 | 0 | 3 | 0 |
بعد ذلك يتم استخدام حساب التشابه بين النصوص من خلال تطبيق المعادلة الرياضية التالية:
التشابه بين النص أ ، والنص ب = (أ × ب) / || أ || × || ب ||
حيث:
أ × ب = مجموع حاصل الضرب الديكارتي لعدد تكرار الكلمات المفتاحية في كل نص
|| أ || = الجذر التربيعي لـ [( تكرار الكلمة الأولى)2 + (تكرار الكلمة الثانية)2 + …..] في النص أ
|| ب || = الجذر التربيعي لـ [(تكرار الكلمة الأولى)2 + (تكرار الكلمة الثانية)2 +….] في النص ب
مثال تطبيقي
في الجدول المبين في الشكل أعلاه، يمكن حساب التشابه بين كل من البحث الأول والبحث الثاني، حيث يتم التعير عنهما بالمتغيرين (أ)، (ب) ويتم التعبير عن كل منهما من خلال عدد مرات ظهور الكلمات المفتاحية فيهما على الترتيب كما يلي:
أ = (5، 0، 3، 0، 2، 0، 0، 2، 0، 0)
ب = (3، 0، 2، 0، 1، 1، 0، 1، 0، 1)
ويكون:
أ × ب = (5 × 3 + 0 × 0 + 3 × 2 + 0 × 0 + 2 × 1 + 0 × 1 + 0 × 0 + 2 × 1 + 0 × 0 + 0 × 1)
= 25
|| أ || = الجذر التربيعي لـ (5 2 + 0 2 + 3 2 + 0 2 + 2 2 + 0 2 + 0 2 + 2 2 + 0 2 + 0 2)
= 6.48
|| ب || = الجذر التربيعي لـ (3 2 + 0 2 + 2 2 + 0 2 + 1 2 + 1 2 + 0 2 + 1 2 + 0 2 + 1 2)
= 4.12
وبتطبيق معادلة حساب التشابه بين البحث (أ) والبحث (ب)، فيكون:
التشابه بين البحث (أ) والبحث (ب) = 25 / (6.48 × 4.12)
= 0.94
أي أن البحث (أ) والبحث (ب) متشابهان بنسبة 94 % تقريبًا وفق هذه الطريقة في القياس.
وفي مجال البحث العلمي، تُستخدم هذه الطريقة في تحكيم الأبحاث العلمية وبحث مدى أصالتها وذلك ضمن مجموعة من معايير تحكيم البحوث العلمية الأكاديمية المعتمدة في المؤسسات الأكاديمية والدوريات العلمية المحكّمة.
المصدر
- كتاب التحليل المتقدم وتنقيب البيانات، د. م. مصطفى عبيد، الطبعة الأولى، دار الفكر العربي، القاهرة، 2017.



