ضرب المتجهات
الأهداف: بنهاية قسم ضرب المتجهات سيكون القارئ قادرًا على:
- شرح الفرق بين حاصل الضرب القياسي وحاصل الضرب الاتجاهي لمتجهين.
- تحديد حاصل الضرب القياسي لمتجهين.
- تحديد حاصل الضرب الاتجاهي لمتجهين.
- وصف كيفية استخدام ضرب المتجهات في الفيزياء.
المحتويات
يمكن ضرب المتجه في متجه آخر ولكن لا يجوز قسمته على متجه آخر. هناك نوعان من أنواع ضرب المتجهات المستخدمة على نطاق واسع في الفيزياء والهندسة. النوع الأول من الضرب هو الضرب القياسي لمتجهين.
ينتج عن الضرب القياسي لمتجهين رقم قياسي (عددي)، كما يشير اسمه. يستخدم الضرب القياسي لتحديد علاقات الشغل والطاقة. على سبيل المثال، يتم تعريف الشغل الذي تؤديه قوة (متجه) على كائن أثناء تسببه في إزاحته (متجه) على أنه حاصل الضرب القياسي لمتجه القوة مع متجه الإزاحة. هناك نوع مختلف تمامًا من الضرب وهو الضرب الاتجاهي للمتجهات. أخذ حاصل الضرب الاتجاهي لمتجهين يعطي لنا نتيجة عبارة عن متجه أيضًا، كما يوحي اسمه. يُستخدم الضرب الاتجاهي لتحديد كميات متجهة مشتقة أخرى. على سبيل المثال، في وصف حركة الدوران، يتم تعريف كمية متجهة تسمى عزم الدوران على أنها حاصل ضرب متجه القوة المؤثرة (متجه) ومسافتها من المحور إلى القوة (متجه). من المهم التمييز بين هذين النوعين من حاصل ضرب المتجهات لأن الضرب القياسي هو كمية قياسية والضرب الاتجاهي هو كمية متجهة.
الضرب القياسي لمتجهين (الضرب النقطي)
ينتج عن الضرب القياسي لمتجهين ناتج عددي.
الضرب القياسي Scalar Product أو الضرب النقطي Dot Product
حاصل الضرب القياسي A⃗ ⋅B⃗ لمتجهين A⃗ , B⃗ هو عدد محدد بالمعادلة (2.27):
(2.27)
حيث φ هي الزاوية بين المتجهات (كما هو موضح في الشكل (2.27). يُطلق على الضرب القياسي أيضًا اسم الضرب النقطي بسبب الترميز النقطي الذي يشير إليه.
في تعريف حاصل الضرب القياسي، لا يهم اتجاه الزاوية، ويمكن قياس φ من أي من المتجهين إلى الآخر لأن:
cos φ = cos (−φ) = cos (2π – φ)
حاصل الضرب النقطي هو عدد سالب عندما يكون:
90 < φ ≤ 180
وهو رقم موجب عندما يكون:
0 < φ ≤ 90
ضرب المتجهات المتوازية والمتعامدة
علاوة على ذلك، حاصل الضرب القياسي لمتجهين متوازيين هو:
وحاصل الضرب القياسي أو النقطي لمتجهين غير متوازيين هو:
يختفي حاصل الضرب القياسي لمتجهين متعامدين:
حاصل الضرب القياسي للمتجه مع نفسه هو مربع مقداره:
(2.28)
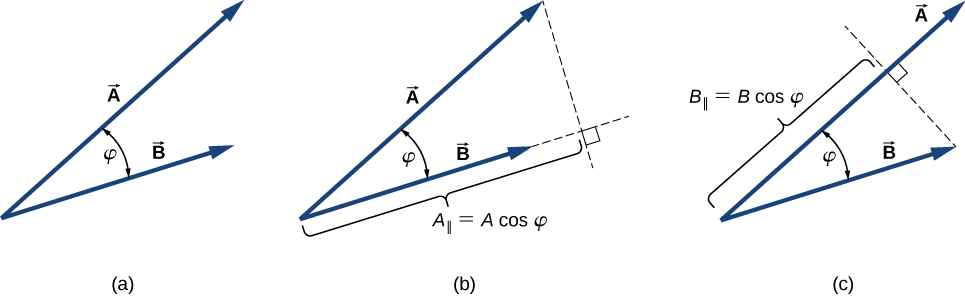
الشكل 2.27: حاصل الضرب القياسي لمتجهين. (a) الزاوية بين المتجهين. (b) الإسقاط المتعامد │A للمتجه A⃗ في اتجاه المتجه B. و(c) الإسقاط المتعامد │B للمتجه B في اتجاه المتجه A.
مثال1: الضرب القياسي للمتجهات
بالنسبة إلى المتجهات الموضحة في الشكل 2.13، أوجد حاص الضرب القياسي A · F.
إستراتيجية الحل
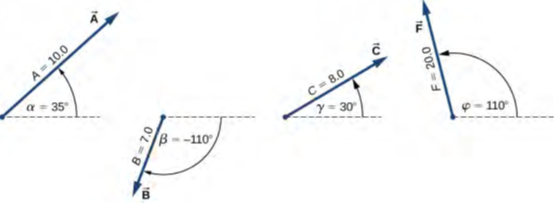
من الشكل 2.13، تكون مقادير المتجهات هي A = 10.0 وF = 20.0. الزاوية θ بينهما هي الفرق: θ = φ – α = 110 – 35 = 75 درجة. يؤدي استبدال هذه القيم في المعادلة 2.27 إلى حاصل الضرب القياسي.
الحل
بالتعويض، تعطينا عمليات الحساب المباشرة:
تحقق من فهمك:
للمتجهات الواردة في الشكل 2.13، أوجد حاصل الضرب القياسي A⃗ ⋅B⃗ و F⃗ ⋅C⃗.
ضرب متجهات الوحدة
في نظام الإحداثيات الديكارتية، يختفي دائمًا حاصل الضرب القياسي لمتجه الوحدة للمحور مع متجهات الوحدة الأخرى للمحاور لأن متجهات الوحدة هذه متعامدة:
(2.29)
في هذه المعادلات، نستخدم حقيقة أن مقادير جميع متجهات الوحدة واحدة:
بالنسبة لمتجهات الوحدة للمحاور، تعطي المعادلة 2.28 التعريفات التالية:
(2.30)
تفسير حاصل الضرب القياسي
يمكن أيضًا تفسير حاصل الضرب القياسي A · B إما على أنه حاصل ضرب B مع الإسقاط المتعامد A⊥ للمتجه A على اتجاه المتجه B (الشكل 2.27 (b)) أو حاصل ضرب A مع الإسقاط المتعامد B⊥ للمتجه B في اتجاه المتجه A (الشكل 2.27 (c)):
على سبيل المثال، في نظام الإحداثيات المستطيل في المستوى، يكون المكون x القياسي للمتجه هو حاصل الضرب النقطي مع متجه الوحدة i^، والمكون القياسي y للمتجه هو حاصل الضرب النقطي مع متجه الوحدة j^:
خصائص الضرب القياسي للمتجهات
الضرب القياسي للمتجهات هو عملية تبادلية:
(2.31)
كما أن ضرب المتجهات القياسي يتبع قانون التوزيع:
(2.32)
يمكننا استخدام قوانين التبادلية والتوزيع لاشتقاق علاقات مختلفة للمتجهات، مثل التعبير عن حاصل الضرب القياسي أو النقطي لمتجهين بدلالة مكوناتهما العددية.
تحقق من فهمك
للمتجه A = Ax i^ + Ay j ^ + Az k^ في نظام إحداثيات ديكارتي مستطيل، استخدم المعادلة 2.29 من خلال المعادلة 2.32 لإظهار أن: A⃗ ⋅iˆ=Ax , A⃗ ⋅jˆ=Ay, A⃗ ⋅kˆ=Az.
حاصل الضرب القياسي بدلالة المكونات
عندما يتم إعطاء المتجهات في المعادلة 2.27 في أشكال مكونات المتجه الخاصة بهم، كما يلي:
يمكننا حساب حاصل ضربهم القياسي على النحو التالي:
القاعدة
الزاوية بين المتجهين
نظرًا لأن الضرب القياسي لمتجهي وحدة مختلفين من المحاور تعطي صفرًا، والضرب القياسي لمتجهات الوحدة مع نفسها تعطي واحدًا (انظر المعادلة 2.29 والمعادلة 2.30)، فلا يوجد سوى ثلاث مصطلحات غير صفرية في هذا التعبير. وهكذا، يمكن تبسيط حاصل الضرب القياسي إلى:
(2.33)
يمكننا استخدام المعادلة 2.33 للضرب القياسي بدلالة المكونات العددية للمتجهات لإيجاد الزاوية بين متجهين. عندما نقسم المعادلة 2.27 على AB، نحصل على معادلة cos φ، التي نستبدل بها المعادلة 2.33:
(2.34)
يتم الحصول على الزاوية φ بين المتجهات A⃗ وB⃗ بأخذ جيب التمام العكسي للتعبير في المعادلة 2.34.
مثال2: الزاوية بين قوتين
تقوم ثلاثة كلاب بسحب عصا في اتجاهات مختلفة، كما هو موضح في الشكل 2.28. يسحب الكلب الأول بقوة F1 = (10.0 i^ – 20.4 j^ + 2.0 k^) N، يسحب الكلب الثاني بقوة F2 = (−15.0 i^ – 6.2 k^) N، والكلب الثالث يسحب بقوة F3 = (5.0 i^ + 12.5 j^) N. ما الزاوية بين القوى F1 و F2؟

إستراتيجية الحل
مكونات متجه القوة F1 هي F1x = 10.0 N و F1y = −20.4 N و F1z = 2.0 N، بينما مكونات متجه القوة F2 هي F2x = −15.0 N و F2y = 0.0 N و F2z = – 6.2 N. يتم حساب حاصل الضرب القياسي لهذه المتجهات ومقاديرها، والتعويض في المعادلة 2.34 ينتج الزاوية المطلوبة.
الحل
مقدار القوى F1 و F2:
وكذلك:
يؤدي استبدال المكونات العددية في المعادلة 2.33 إلى إنتاج حاصل الضرب القياسي:
إيجاد الزاوية
أخيرًا، نقوم باستبدال كل شيء والتعويض في المعادلة 2.34 نحصل على الزاوية:
الدلالة
لاحظ أنه عندما يتم إعطاء المتجهات بدلالة متجهات الوحدة للمحاور، يمكننا إيجاد الزاوية بينهما دون معرفة التفاصيل الخاصة بالاتجاهات الجغرافية التي تمثلها متجهات الوحدة. هنا، على سبيل المثال، قد يكون اتجاه المحور السيني + x إلى الشرق. وقد يكون اتجاه المحور الصادي + y إلى الشمال. لكن الزاوية بين القوتين في المسألة ستكون هي نفسها حتى إذا كان الاتجاه + x إلى الغرب والاتجاه + y إلى الجنوب.
تحقق من فهمك
أوجد الزاوية بين القوى F1 و F3 في المثال السابق.
مثال3: الشغل والقوة
عندما تسحب القوة F جسمًا وعندما تتسبب في إزاحته D، نقول إن القوة تؤدي شغلاً. مقدار الشغل الذي تقوم به القوة هو حاصل الضرب القياسي للمتجهين F · D. إذا تحركت العصا في المثال 2 مؤقتًا وتم إزاحتها بواسطة المتجه D = (−7.9 j^ – 4.2 k^) cm. فما مقدار الشغل الذي قام به الكلب الثالث في المثال 2؟
إستراتيجية الحل
نحسب حاصل الضرب القياسي لمتجه الإزاحة D مع متجه القوة F3 = (5.0 i^ + 12.5 j^)N، والذي هو قوة السحب من الكلب الثالث. دعنا نستخدم الرمز W3 للإشارة إلى الشغل المنجز بالقوة F3 عند الإزاحة D.
الحل
لحساب الشغل نقوم بتطبيق مباشر لحاصل الضرب القياسي أو النقطي:
أي أن الشغل المبذول = -98.7 نيوتن . سم.
الدلالة
تسمى وحدة قياس الشغل في النظام الدولي للوحدات (SI) الجول ويُرمز لها بالرمز (J)، حيث:
1 J = 1 N · m
أما الوحدة cm · N يمكن كتابتها في صورة: 10-2 (m · N) = 10−2 J، لذلك يمكن التعبير عن الإجابة بالشكل التالي:
W3 = − 0.9875 J ≈ −1.0 J
تحقق من فهمك
ما مقدار الشغل الذي قام به الكلب الأول والكلب الثاني في المثال 2 بشأن الإزاحة المذكورة في المثال 3؟
حاصل الضرب الاتجاهي لمتجهين (الضرب التقاطعي)
ينتج عن الضرب الاتجاهي لمتجهين متجه جديد.
الضرب الاتجاهي Vector Product أو الضرب التقاطعي Cross Product:
يتم الإشارة إلى الضرب الاتجاهي لمتجهين A و B بواسطة A × B وغالبًا ما يشار إليه على أنه ضرب تقاطعي. حاصل الضرب الاتجاهي هو متجه له اتجاه عمودي على كلا المتجهين A و B. بمعنى آخر، المتجه A × B عمودي على المستوى الذي يحتوي على المتجهات A و B، كما هو موضح في الشكل 2.29.
يتم تحديد مقدار حاصل الضرب الاتجاهي على أنه:
(2.35)
حيث يتم قياس الزاوية φ، بين المتجهين، من المتجه A (المتجه الأول في حاصل الضرب) إلى المتجه B (المتجه الثاني في حاصل الضرب)، كما هو موضح في الشكل 2.29، وهذه الزاوية تتراوح بين صفر درجة و180 درجة.
وفقًا للمعادلة 2.35، يختفي حاصل الضرب الاتجاهي لأزواج المتجهات التي تكون إما متوازية φ = 0 أو متعاكسة ومتوازية φ = 180 وذلك لأن sin 0 = sin 180 = 0.
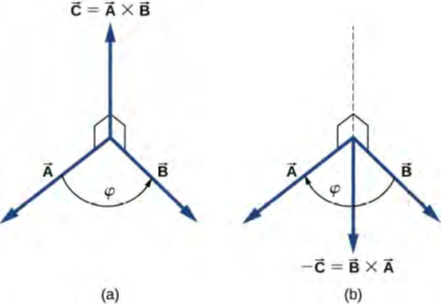
الشكل 2.29: حاصل الضرب الاتجاهي لمتجهين مرسوم في فضاء ثلاثي الأبعاد. (a) حاصل الضرب الاتجاهي A⃗ × B⃗ هو متجه عمودي على المستوى الذي يحتوي على المتجهات A وB. تشير المربعات الصغيرة المرسومة في المنظور إلى الزوايا اليمنى بين A⃗ وC، وبين B⃗ وC بحيث إذا كانت A⃗ وB⃗ مستوية على الأرض، فإن المتجه C يشير عموديًا إلى السقف. (b) حاصل الضرب الاتجاهي B × A⃗ هو متجه موازٍ للمتجه A⃗ × B⃗.
خصائص الضرب الاتجاهي
على الخط العمودي على المستوى الذي يحتوي على المتجهات A⃗ و B⃗ هناك اتجاهان بديلين – إما لأعلى أو لأسفل، كما هو موضح في الشكل 2.29 – وقد يكون اتجاه حاصل الضرب الاتجاهي أحدهما. في الاتجاه القياسي الأيمن، حيث يتم قياس الزاوية بين المتجهات عكس اتجاه عقارب الساعة من المتجه الأول، يشير المتجه A⃗ × B⃗ إلى الأعلى، كما هو موضح في الشكل 2.29 (a). إذا عكسنا ترتيب الضرب، بحيث يأتي الآن B⃗ أولاً في الضرب، فيجب أن يشير المتجه B⃗ × A⃗ إلى الأسفل، كما هو موضح في الشكل 2.29 (b). هذا يعني أن المتجهات A⃗ × B⃗ و B⃗ × A⃗ متعاكسة مع بعضها البعض وأن الضرب الاتجاهي ليس تبادليًا ولكنه مضاد للتبادل. تعني الخاصية المضادة للتبادل أن الضرب الاتجاهي يعكس العلامة عندما يتم عكس ترتيب الضرب، أي أن:
(2.36)
قاعدة المفتاح الأيمن
قاعدة المفتاح الأيمن عبارة عن ذاكرة شائعة تستخدم لتحديد اتجاه حاصل الضرب الاتجاهي. كما هو موضح في الشكل 2.30، يتم وضع المفتاح في اتجاه عمودي على المستوى الذي يحتوي على المتجهات A و B، ويتم تدوير مقبضه في الاتجاه من المتجه الأول إلى الثاني في حاصل الضرب. يتم تحديد اتجاه حاصل الضرب الاتجاهي ( أو التقاطعي) من خلال اتجاه تقدم المفتاح.
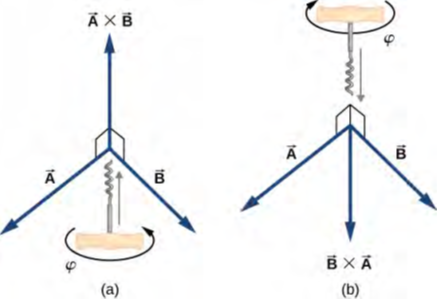
الشكل 2.30: يمكن استخدام قاعدة المفتاح الأيمن لتحديد اتجاه حاصل الضرب الاتجاهي (أو التقاطعي) A × B. ضع المفتاح في الاتجاه العمودي للمستوى الذي يحتوي على المتجهات A وB، وأدره في الاتجاه من المتجه الأول إلى الثاني في حاصل الضرب. يتم تحديد اتجاه حاصل الضرب الاتجاهي من خلال اتجاه تقدم المفتاح. (a) تعني الحركة الصعودية أن متجه حاصل الضرب يشير لأعلى. (b) تعني الحركة الهبوطية أن متجه حاصل الضرب العكسي يشير إلى أسفل.
مثال4: عزم القوة
الميزة الميكانيكية التي توفرها أداة مألوفة تسمى مفتاح الربط (الشكل 2.31) تعتمد على قيمة F للقوة المطبقة، وعلى اتجاهها فيما يتعلق بمقبض مفتاح الربط، وعلى مدى بُعد هذه القوة عن الصمولة. يتم تمثيل المسافة R من الصمولة إلى النقطة التي يتصل بها متجه القوة F بالمتجه الشعاعي R. كمية المتجه الفيزيائية التي تجعل الصمولة تدور تسمى عزم الدوران (يُشار إليها بالمتجه τ)، وهي حاصل الضرب الاتجاهي للمسافة بين المحور والقوة في القوة: τ = R × F.
لفك صمولة صدئة، يتم تطبيق قوة مقدارها 20.00 نيوتن على مقبض مفتاح الربط بزاوية φ = 40 درجة وعلى مسافة 0.25 متر من الصمولة، كما هو موضح في الشكل 2.31 (a). أوجد مقدار واتجاه عزم الدوران المطبق على الصمولة.
ماذا سيكون حجم واتجاه عزم الدوران إذا تم تطبيق القوة بزاوية φ = 45 درجة، كما هو موضح في الشكل 2.31 (b)؟ ما قيمة الزاوية φ التي يملكها أكبر مقدار لعزم الدوران؟
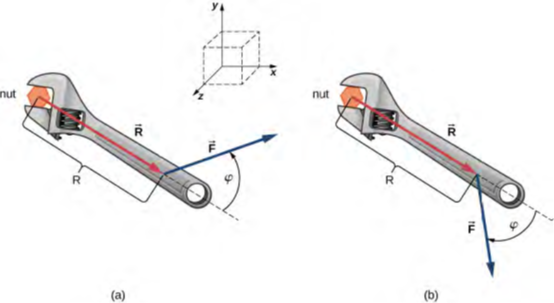
الشكل 2.31: مفتاح الربط يوفر قبضة وميزة ميكانيكية في تطبيق عزم الدوران لتدوير الصمولة. (a) انعطف عكس اتجاه عقارب الساعة لفك الصامولة. (b) لفه في اتجاه عقارب الساعة لربط الصامولة.
إستراتيجية الحل
نعتمد الإطار المرجعي الموضح في الشكل 2.31، حيث تكمن المتجهات R وF في المستوى xy ويكون الأصل في موضع الصمولة. الاتجاه الشعاعي على طول المتجه R (الإشارة بعيدًا عن الأصل) هو الاتجاه المرجعي لقياس الزاوية φ لأن R هو المتجه الأول في حاصل الضرب الاتجاهي τ = R × F. يجب أن يقع المتجه τ على طول المحور z لأن هذا هو المحور العمودي على المستوى xy، حيث يقع كل من R وF. لحساب مقدار τ، نستخدم المعادلة 2.35. للعثور على اتجاه τ، نستخدم قاعدة المفتاح الأيمن (الشكل 2.30).
الحل
للحالة في (a)، تعطي قاعدة المفتاح اتجاه R × F في الاتجاه الموجب للمحور z.
فيزيائيًا، فهذا يعني أن متجه عزم الدوران τ يشير إلى خارج الصفحة، عموديًا على مقبض مفتاح الربط. نحدد F = 20.00 N و R = 0.25 متر، ونحسب المقدار باستخدام المعادلة 2.35:
للحالة في (b)، تعطي قاعدة المفتاح اتجاه R × F في الاتجاه السالب للمحور z. فيزيائيًا، فهذا يعني أن المتجه τ يشير إلى داخل الصفحة، عموديًا على مقبض مفتاح الربط. مقدار هذا العزم هو:
يكون لعزم الدوران أكبر قيمة عندما تكون sin φ = 1، والتي تحدث عندما تكون φ = 90 درجة. فيزيائيًا، فهذا يعني أن مفتاح الربط هو الأكثر فاعلية – مما يمنحنا أفضل ميزة ميكانيكية – عندما نطبق القوة بشكل عمودي على مقبض مفتاح الربط. بالنسبة للموقف في هذا المثال، فإن أفضل قيمة لعزم الدوران هي:
الدلالة
عند حل مسائل الميكانيكا، لا نحتاج غالبًا إلى استخدام قاعدة المفتاح على الإطلاق، كما سنرى الآن في الحل المكافئ التالي. لاحظ أنه بمجرد تحديد المتجه R × F يقع على طول المحور z، يمكننا كتابة هذا المتجه بدلالة متجه الوحدة k^ للمحور z:
في هذه المعادلة، الرقم الذي يضرب k^ هو المكون القياسي z للمتجه R × F. في حساب هذا المكون، يجب الحرص على قياس الزاوية φ عكس اتجاه عقارب الساعة من R (المتجه الأول) إلى F (المتجه الثاني). باتباع هذا المبدأ للزوايا، نحصل على RF sin (+40) = + 3.2 N · m للحالة في (a)، ونحصل على RF sin (−45) = −3.5 N · m للوضع في (b).
في الحالة الأخيرة، تكون الزاوية سالبة لأن الرسم البياني في الشكل 2.31 يشير إلى أن الزاوية تقاس في اتجاه عقارب الساعة؛ ولكن، يتم الحصول على نفس النتيجة عند قياس هذه الزاوية عكس اتجاه عقارب الساعة لأن + (360 درجة – 45 درجة) = + 315 درجة وجيب (+ 315 درجة) = جيب (45 درجة). بهذه الطريقة، نحصل على الحل دون الرجوع إلى قاعدة المفتاح. بالنسبة للحالة في (a)، يكون الحل هو R × F = + 3.2 N · m k^؛ للحالة في (b)، الحل هو R × F = −3.5 N · m k^.
تحقق من فهمك
للمتجهات الواردة في الشكل 2.13، أوجد حاصل الضرب الاتجاهي: A⃗ ×B⃗ و C⃗ ×F⃗.
خاصية التوزيع في ضرب المتجهات
على غرار حاصل الضرب القياسي أو النقطي (المعادلة 2.32)، فإن حاصل الضرب الاتجاهي (أو التقاطعي) له خاصية التوزيع التالية:
(2.37)
يتم تطبيق خاصية التوزيع بشكل متكرر عندما يتم التعبير عن المتجهات باستخدام مكوناتها، بدلالة متجهات الوحدة للمحاور الديكارتية.
عندما نطبق تعريف الضرب الاتجاهي، المعادلة 2.35، على متجهات الوحدة i^ و j^ و k^ التي تحدد اتجاهات x و y و z الموجبة في الفراغ، نجد أن:
(2.38)
يجب أن تكون جميع حواصل الضرب الاتجاهي الأخرى لمتجهات الوحدات الثلاث متجهات ذات مقادير وحدة لأن i^ و j^ و k^ متعامدة. على سبيل المثال، بالنسبة للزوج i^ و j^، المقدار هو:
اتجاه حاصل الضرب
يجب أن يكون اتجاه حاصل الضرب الاتجاهي i^ × j^ متعامدًا مع المستوى xy، مما يعني أنه يجب أن يكون على طول المحور z. متجهات الوحدة الوحيدة على طول المحور z هي +k^ أو -k^. وفقًا لقاعدة المفتاح، يجب أن يكون اتجاه المتجه i^ × j^ موازيًا لمحور z الموجب. لذلك، نتيجة الضرب i^ × j^ مطابقة لـ + k^. يمكننا تكرار نفس المنطق للأزواج المتبقية من متجهات الوحدة. نتائج حاصل الضرب لتلك الأزواج هي:
(2.39)
الترتيب الدوري لمتجهات الوحدة
لاحظ أنه في المعادلة 2.39، تظهر متجهات الوحدات الثلاثة i^ و j^ و k^ بالترتيب الدوري الموضح في الرسم التخطيطي في الشكل 2.32 (a). يعني الترتيب الدوري أنه في صيغة حاصل الضرب، i^ يتبع k^ ويأتي قبل j^، أو k^ يتبع j^ ويأتي قبل i^، أو j^ يتبع i^ ويأتي قبل k^. حاصل الضرب الاتجاهي لمتجهي وحدة مختلفين هو دائمًا متجه وحدة ثالث. عندما يظهر متجهان للوحدة في الضرب الاتجاهي بالترتيب الدوري، فإن نتيجة هذا الضرب هي متجه الوحدة المتبقي في نفس الترتيب، كما هو موضح في الشكل 2.32 (b).
عندما تظهر متجهات الوحدة في الضرب الاتجاهي بترتيب مختلف، تكون النتيجة متجه الوحدة الذي يكون عكسيًا لمتجه الوحدة المتبقي (أي تكون النتيجة بعلامة الطرح، كما هو موضح في الأمثلة في الشكل 2.32 (c) والشكل 2.32 (d): من الناحية العملية، عندما تكون المهمة هي العثور على حاصل الضرب الاتجاهي للمتجهات المعطاة في شكل مكون متجه، فإن هذه القاعدة لعمليات الضرب الاتجاهي لمتجهات الوحدة مفيدة جدًا.
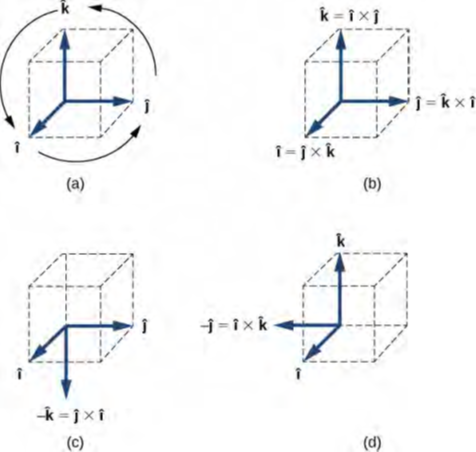
الشكل 2.32: (a) الرسم التخطيطي للترتيب الدوري لمتجهات الوحدة للمحاور. (b) حاصل الضرب الاتجاهي الوحيد حيث تظهر متجهات الوحدة بالترتيب الدوري. حواصل الضرب هذه لها علامة موجبة. (c, d) مثالان على حواصل الضرب الاتجاهية حيث لا تظهر متجهات الوحدة بالترتيب الدوري. حواصل الضرب الاتجاهي هذه لها علامة سالبة.
المكونات العددية لحاصل الضرب الاتجاهي
لنفترض أننا نريد إيجاد حاصل الضرب الاتجاهي A × B للمتجهات A = Axi^ + Ayj^ + Azk^ والمتجه B = Bx i^ + By j^ + Bz k^. يمكننا استخدام خاصية التوزيع (المعادلة 2.37)، والخاصية المضادة للتبادل (المعادلة 2.36)، والضرب الاتجاهي في المعادلة 2.38 والمعادلة 2.39 لمتجهات الوحدة لإجراء الجبر التالي:
ملاحظة
عند إجراء عمليات جبرية على المتجهات تتضمن حاصل الضرب الاتجاهي، كن حذرًا جدًا بشأن الحفاظ على الترتيب الصحيح للضرب لأن حاصل الضرب الاتجاهي مضاد للتبادل. الخطوتان الأخيرتان اللتان لا يزال يتعين علينا القيام بهما لإكمال مهمتنا هما، أولاً، تجميع الحدود التي تحتوي على متجه وحدة مشترك، وثانيًا، التحليل إلى عوامل. بهذه الطريقة نحصل على التعبير التالي المفيد للغاية لحساب الضرب الاتجاهي:
(2.40)
في هذا التعبير، تكون المكونات العددية لمتجه حاصل الضرب الاتجاهي هي:
(2.41)
عند إيجاد حاصل الضرب الاتجاهي، من الناحية العملية، يمكننا استخدام إما المعادلة 2.35 أو المعادلة 2.40، اعتمادًا على أي منهما يبدو أقل تعقيدًا من الناحية الحسابية. كلاهما يؤدي إلى نفس النتيجة النهائية. طريقة واحدة للتأكد من أن النتيجة النهائية صحيحة هي استخدام كليهما.
مثال5: جسيم في مجال مغناطيسي
عند التحرك في مجال مغناطيسي، قد تتعرض بعض الجسيمات لقوة مغناطيسية. بدون الخوض في التفاصيل – تأتي دراسة مفصلة للظواهر المغناطيسية في فصول لاحقة – دعنا نعترف بأن المجال المغناطيسي B هو متجه، والقوة المغناطيسية F هي كمية متجهة، وسرعة الجسيم u متجه. يتناسب متجه القوة المغناطيسية مع حاصل الضرب الاتجاهي لمتجه السرعة مع متجه المجال المغناطيسي، والذي نعبر عنه كما يلي: F = ζ u × B. في هذه المعادلة، يعتني الثابت باتساق الوحدات الفيزيائية، لذلك يمكننا حذف الوحدات الفيزيائية للمتجهات u وB. في هذا المثال، لنفترض أن الثابت ζ هو موجب.
جسيم يتحرك في الفضاء مع متجه السرعة u = −5.0 i^ – 2.0 j^ + 3.5 k^ ويدخل منطقة ذات مجال مغناطيسي ويختبر قوة مغناطيسية. أوجد القوة المغناطيسية F المؤثرة على هذا الجسيم عند نقطة الدخول إلى المنطقة حيث يكون متجه المجال المغناطيسي:
B = 7.2 i^ – j^ – 2.4 k^
B = 4.5 k^
في كل حالة، أوجد المقدار F للقوة المغناطيسية والزاوية θ لمتجه القوة F التي يصنعها مع متجه المجال المغناطيسي المحدد B⃗.
إستراتيجية الحل
أولاً، نريد إيجاد حاصل الضرب الاتجاهي u × B، لأنه بعد ذلك يمكننا تحديد القوة المغناطيسية باستخدام المعادلة F = ζ u × B. يمكن إيجاد مقدار F إما باستخدام المكونات:
أو عن طريق حساب المقدار |u × B| مباشرة باستخدام المعادلة 2.35. في النهج الأخير، علينا إيجاد الزاوية بين المتجهين u وB. عندما يكون لدينا F، فإن الطريقة العامة لإيجاد زاوية الاتجاه θ تتضمن حساب حاصل الضرب القياسي F · B والتعويض في المعادلة 2.34. لحساب حاصل الضرب الاتجاهي، يمكننا إما استخدام المعادلة 2.40 أو حساب حاصل الضرب الاتجاهي مباشرة، أيهما أسهل.
الحل
مكونات متجه السرعة هي:
ux = −5.0, uy = −2.0, uz = 3.5
الحالة الأولى (أ)
مكونات متجه المجال المغناطيسي هي Bx = 7.2، By = -1.0، و Bz = −2.4. بالتعويض في المعادلة 2.41 ينتج المكونات العددية للمتجه F = ζ u × B:
وبالتالي، فإن متجه القوة المغناطيسية يساوي:
F = ζ(8.3 i^ + 13.2 j^ + 19.4 k^)
ومقداره العددي هو:
حساب الزاوية
لحساب الزاوية θ، قد نحتاج إلى إيجاد مقدار متجه المجال المغناطيسي:
وحاصل الضرب القياسي F · B:
الآن، بالتعويض في المعادلة 2.34 نحصل على الزاوية θ:
ومن ثم، فإن متجه القوة المغناطيسية يكون عموديًا على متجه المجال المغناطيسي. (كان بإمكاننا توفير بعض الوقت إذا قمنا بحساب حاصل الضرب القياسي مسبقًا).
الحالة الثانية (ب)
نظرًا لأن المتجه B = 4.5 k^ يحتوي على مكون واحد فقط، يمكننا إجراء الجبر بسرعة والعثور على حاصل الضرب الاتجاهي مباشرةً:
ومقدار القوة المغناطيسية هو:
ولأن حاصل الضرب القياسي يساوي صفر:
لذا فإن متجه القوة المغناطيسية F عمودي على متجه المجال المغناطيسي B.
الدلالة
حتى بدون حساب حاصل الضرب القياسي فعليًا، يمكننا أن نتنبأ بأن متجه القوة المغناطيسية يجب أن يكون دائمًا متعامدًا على متجه المجال المغناطيسي بسبب طريقة تكوين هذا المتجه. على وجه التحديد، متجه القوة المغناطيسية هو حاصل الضرب الاتجاهي F = ζ u × B، وبحسب تعريف حاصل الضرب الاتجاهي (انظر الشكل 2.29)، يجب أن يكون المتجه F عموديًا على كلا المتجهين u وB.
تحقق من فهمك
بالنظر إلى المتجهين A = − i^ + j^ والمتجه B = 3 i^ – j^، أوجد (أ) A × B ، (ب) |A × B|، (ج) الزاوية بين A وB، (د) الزاوية بين A × B والمتجه C = i^ + k^.
في ختام هذا القسم الخاص بموضوع ضرب المتجهات، نريد التأكيد على أن “حاصل الضرب القياسي أو حاصل الضرب النقطي” و”حاصل الضرب الاتجاهي أو حاصل الضرب التقاطعي” هما كائنات رياضية مختلفة تمامًا لها معاني مختلفة. حاصل الضرب القياسي هو كمية قياسية عددية؛ أما حاصل الضرب الاتجاهي هو كمية متجهة. تستخدم الفصول اللاحقة المصطلحين “الضرب القياسي” و”الضرب النقطي” بشكل تبادلي وهما بنفس المعنى. وبالمثل، يتم استخدام المصطلحين “الضرب الاتجاهي” أو “الضرب التقاطعي” بشكل تبادلي وهما بنفس المعنى.
المصدر
- موسوعة الفيزياء العامة، ترجمة وإعداد: د. م. مصطفى عبيد، مركز البحوث والدراسات متعدد التخصصات، 2022.
- كتاب الفيزياء للجامعات، صموئيل جيه لينغ، جامعة ولاية ترومان، د. جيف ساني، جامعة لويولا ماريماونت ويليام مويبس.
