المحتويات
الإحداثيات القطبية للمتجهات في بعدين
لوصف مواقع النقاط أو المتجهات في المستوى، نحتاج إلى اتجاهين متعامدين. في نظام الإحداثيات الديكارتية، يتم إعطاء هذه الاتجاهات بواسطة متجهات الوحدة i ^ و j ^ على طول المحور x والمحور y، على التوالي. يعتبر نظام الإحداثيات الديكارتية مناسبًا جدًا للاستخدام في وصف عمليات الإزاحة والسرعات للأشياء والقوى المؤثرة عليها. ومع ذلك، يصبح الأمر مرهقًا عندما نحتاج إلى وصف دوران الكائنات. عند وصف الدوران، عادة ما نعمل في نظام الإحداثيات القطبية أو Polar Coordinates.
في نظام الإحداثيات القطبية، يتم تحديد موقع النقطة P في المستوى بواسطة إحداثيات قطبية (الشكل 2.20). أول إحداثي قطبي هو الإحداثي الشعاعي r، وهو مسافة النقطة P من الأصل. الإحداثي القطبي الثاني هو الزاوية φ التي يصنعها المتجه الشعاعي مع اتجاه معين، وعادة ما يكون اتجاه الموجب لمحور x. في الإحداثيات القطبية، تُقاس الزوايا بوحدات الراديان أو الراديان. يتم إرفاق المتجه الشعاعي في الأصل والنقاط بعيدًا عن الأصل إلى النقطة P. يتم وصف هذا الاتجاه الشعاعي بواسطة وحدة متجه شعاعي r ^. متجه الوحدة الثانية t ^ هو متجه متعامد مع الاتجاه الشعاعي r ^. يشير الاتجاه الموجب + t ^ إلى كيفية تغير الزاوية في اتجاه عكس اتجاه عقارب الساعة. بهذه الطريقة، يمكن وصف النقطة P التي لها إحداثيات (x, y) في النظام المستطيل بشكل مكافئ في نظام الإحداثيات القطبية بواسطة الإحداثيين القطبين (r, φ).
المعادلة 2.17 صالحة لأي متجه، لذا يمكننا استخدامها للتعبير عن إحداثيات x و y للمتجه r →. بهذه الطريقة نحصل على العلاقة بين الإحداثيات القطبية والإحداثيات المستطيلة للنقطة P:
x = r cos φ
y = r sin φ
(2.18)
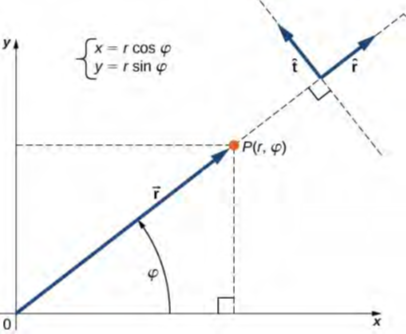
الشكل 2.20 باستخدام الإحداثيات القطبية، يحدد متجه الوحدة r ^ الاتجاه الموجب على طول نصف القطر r (الاتجاه الشعاعي)، وبشكل متعامد معه، يحدد متجه الوحدة t ^ الاتجاه الإيجابي للدوران بالزاوية φ.
مثال1: على الإحداثيات القطبية في بعدين
يجد صائد الكنوز عملة فضية واحدة في موقع يبعد 20.0 متر عن بئر جاف في اتجاه 20 درجة شمال شرق ويعثر على عملة ذهبية واحدة في موقع يبعد 10.0 متر عن البئر في اتجاه 20 درجة شمال الغرب. ما هي الإحداثيات القطبية والديكارتية المستطيلة لهذه الاكتشافات بالنسبة للبئر؟
إستراتيجية الحل
يشير البئر إلى أفضل أصل لنظام الإحداثيات والشرق وهو اتجاه المحور السيني الموجب x-direction. نحدد المسافات الشعاعية من المواقع إلى الأصل، وهي rS = 20.0 م (للعملة الفضية) و rG = 10.0 م (للعملة الذهبية). لإيجاد الإحداثيات الزاوية، نحول 20 درجة إلى راديان: 20 درجة = π20 / 180 = π / 9. نستخدم المعادلة 2.18 لإيجاد إحداثيات x و y للعملات المعدنية.
الحل
الإحداثي الزاوي للعملة الفضية هو φS = π / 9، في حين أن الإحداثي الزاوي للعملة الذهبية هو φG = π – π / 9 = 8π / 9. ومن ثم، فإن الإحداثيات القطبية للعملة الفضية هي: ((rS, φS = (20.0 m, π / 9) وتلك الخاصة بالعملة الذهبية هي: ((rG, φG = (10.0 m, π / 9). نعوض بهذه الإحداثيات في المعادلة 2.18 للحصول على الإحداثيات الديكارتية المستطيلة. بالنسبة للعملة الذهبية، تكون الإحداثيات:
xG = rG cos φG = (10.0 m) cos 8π/9 = −9.4 m
yG = rG sin φG = (10.0 m) sin 8π/9 = 3.4 m
⇒ (xG, yG) = (−9.4 m, 3.4 m)
بالنسبة للعملة الفضية، فإن الإحداثيات هي:
xS = rS cos φS = (20.0 m) cos π/9 = 18.9 m
yS = rS sin φS = (20.0 m) sin π/9 = 6.8 m
⇒ (xS, yS) = (18.9 m, 6.8 m)
الإحداثيات القطبية للمتجهات في ثلاثة أبعاد
لتحديد موقع نقطة في الفضاء، نحتاج إلى ثلاث إحداثيات (x, y, z)، حيث تحدد الإحداثيات x و y مواقع في المستوى، والإحداثيات z تعطي موضعًا رأسيًا أعلى أو أسفل المستوى. يحتوي الفضاء ثلاثي الأبعاد على ثلاث اتجاهات متعامدة، لذلك لا نحتاج إلى متجهين بل ثلاث وحدات لتحديد نظام إحداثيات ثلاثي الأبعاد. في نظام الإحداثيات الديكارتية، أول متجهين للوحدة هما متجه الوحدة لمحور x i^ ومتجه الوحدة للمحور y j^. متجه الوحدة الثالثة k ^ هو اتجاه المحور زاي أو z (الشكل 2.21). يعد الترتيب الذي يتم فيه تسمية المحاور، وهو الترتيب الذي تظهر به متجهات الوحدات الثلاثة، أمرًا مهمًا لأنه يحدد اتجاه نظام الإحداثيات. يحدد الترتيب x-y-z، الذي يكافئ الترتيب i ^ – j ^ – k ^، نظام الإحداثيات القياسي الأيمن (التوجيه الإيجابي).
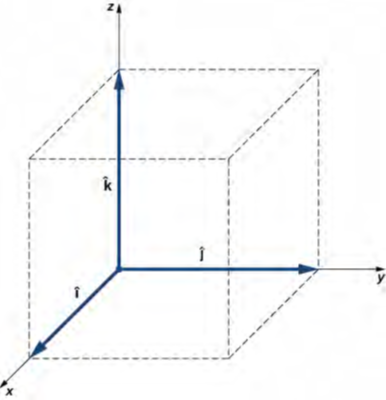
الشكل 2.21 ثلاث متجهات وحدة تحدد نظامًا ديكارتيًا في فضاء ثلاثي الأبعاد. يحدد الترتيب الذي تظهر به نواقل الوحدة هذه اتجاه نظام الإحداثيات. الترتيب الموضح هنا يحدد اتجاه اليد اليمنى.
تحليل المتجه في ثلاثة أبعاد
في الفضاء ثلاثي الأبعاد، يحتوي المتجه A → على ثلاثة مكونات متجهة: المكون x A → x = Ax i^، وهو جزء من المتجه A → على طول المحور x؛ المكون y A → y = Ay j^، وهو جزء من A → على طول المحور y؛ والمكون z A → z = Az k^، وهو جزء من المتجه على طول المحور z. المتجه في الفضاء ثلاثي الأبعاد هو المجموع المتجه لمكوناته أو مركباته المتجهية الثلاثة (الشكل 2.22):
A → = Ax i ^ + Ay j ^ + Azk ^
(2.19)
إذا علمنا إحداثيات نقطة الأصل له b(xb, yb, zb) ونهايته e(xe, ye, ze)، يتم الحصول على مكوناته العددية بأخذ الفرق بينهما: يتم إعطاء المكونات Ax و Ay بواسطة المعادلة 2.13 والمكون Az يعطى بواسطة المعادلة:
Az = ze − zb
(2.20)
يتم الحصول على مقدار المتجه A بتعميم المعادلة 2.15 على ثلاثة أبعاد:
A = Sqrt [Ax 2 + Ay 2 + Az 2]
(2.21)
يأتي هذا التعبير عن مقدار المتجه من تطبيق نظرية فيثاغورس مرتين. كما هو موضح في الشكل 2.22، فإن القطر في المستوى xy له طول = Sqrt [Ax2 + Ay2] ويضاف مربعه إلى المربع Az2 ليعطي A2. لاحظ أنه عندما يكون المكون z هو صفر، فإن المتجه يقع بالكامل في المستوى xy ويتم تقليص وصفه أو تحليله إلى بعدين.
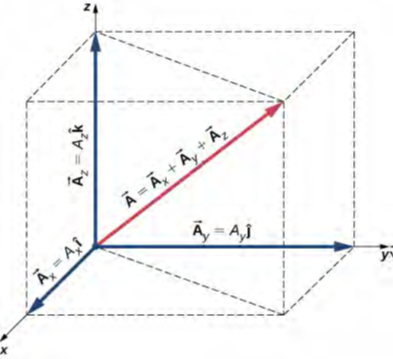
الشكل 2.22: المتجه في الفضاء ثلاثي الأبعاد هو مجموع متجه لمكوناته الثلاثة المتجهية
مثال2: إقلاع طائرة بدون طيار
أثناء إقلاع الطائرة بدون طيار هيرون أو Heron (الشكل 2.23)، يكون موقع الطائرة بالنسبة لبرج المراقبة 100 متر فوق سطح الأرض، و300 متر في الشرق، و200 متر في الشمال. بعد دقيقة واحدة، وصل موقعها إلى 250 م عن سطح الأرض، و1200 م في الشرق، و2100 م في الشمال. ما هو متجه إزاحة الطائرة بدون طيار بالنسبة لبرج التحكم؟
ما مقدار متجه الإزاحة؟

الشكل 2.23 الطائرة بدون طيار IAI Heron أثناء الطيران
استراتيجية الحل
بواسطة متجه الوحدة i^ إلى الشرق، يتم إعطاء الاتجاه الموجب + للمحور الصادي y بواسطة متجه الوحدة j ^ إلى الشمال، ويتم إعطاء الاتجاه الموجب لمحور z بواسطة متجه الوحدة k^، والذي يشير إلى اتجاه الأعلى من الأرض. الموضع الأول للطائرة بدون طيار هو أصل (أو، على نحو مكافئ، البداية) لمتجه الإزاحة وموضعها الثاني هو نهاية متجه الإزاحة.
الحل
نحدد نقاط البداية والنهاية كما يلي:
b(300.0 m, 200.0 m, 100.0 m)
e(1200 m, 2100 m, 250 m)
ونستخدم المعادلة 2.13 والمعادلة 2.20 للعثور على المكونات العددية لمتجه إزاحة الطائرة بدون طيار:
Dx = xe − xb = 1200.0 m − 300.0 m = 900.0 m
Dy = ye − yb = 2100.0 m − 200.0 m = 1900.0 m
and
Dz = ze − zb = 250.0 m − 100.0 m = 150.0 m
نستبدل هذه المكونات في المعادلة 2.19 لإيجاد متجه الإزاحة أو قيمته المتجهة:
D→ = Dx i^ + Dy j^ + Dz k^ = 900.0 m i^ + 1900.0 m j^ + 150.0 m k^
D → = (0.90 i^ + 1.90 j^ + 0.15 k^) km.
نعوض في المعادلة 2.21 لإيجاد مقدار الإزاحة أو قيمتها العددية:
D = Sqrt [Dx2 + Dy2 + Dz2] = (0.90 km)2 + (1.90 km)2 + (0.15 km)2 = 2.11 km
تحقق من فهمك
إذا كان متوسط متجه السرعة للطائرة بدون طيار في الإزاحة في المثال 2.7 هو:
u → = (15.0 i^ + 31.7 j^ + 2.5 k^) m/s
فما هو مقدار متجه سرعة الطائرة بدون طيار؟
المصدر
- موسوعة الفيزياء العامة، ترجمة وإعداد: د. م. مصطفى عبيد، مركز البحوث والدراسات متعدد التخصصات، 2022.
- كتاب الفيزياء للجامعات، صموئيل جيه لينغ، جامعة ولاية ترومان، د. جيف ساني، جامعة لويولا ماريماونت ويليام مويبس.
